Moyenne pythagoricienne

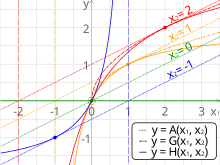
En mathématiques, les trois moyennes pythagoriciennes sont la moyenne arithmétique (A), la moyenne géométrique (G) et la moyenne harmonique (H). Ces moyennes ont été étudiées avec proportions par les Pythagoriciens et des générations suivantes de mathématiciens grecs^[1] de par leur importance en géométrie et en musique.

Définition

On définit les moyennes arithmétique, géométrique et harmonique, comme suit respectivement :

${\displaystyle {\begin{aligned}\operatorname {A} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {x_{1}+\;\cdots \;+x_{n}}{n}}\\[9pt]\operatorname {G} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\sqrt[{n}]{\left\vert x_{1}\times \,\cdots \,\times x_{n}\right\vert }}\\[9pt]\operatorname {H} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {n}{\displaystyle {\frac {1}{x_{1}}}+\;\cdots \;+{\frac {1}{x_{n}}}}}\end{aligned}}}$

Propriétés

Chaque moyenne, M, vérifie les propriétés suivantes :

Homogénéité d'ordre 1

${\displaystyle \operatorname {M} (bx_{1},\,\ldots ,\,bx_{n})=b\operatorname {M} (x_{1},\,\ldots ,\,x_{n})}$

Invariance par permutation

${\displaystyle \forall i,j,\quad \operatorname {M} (\ldots ,\,x_{i},\,\ldots ,\,x_{j},\,\ldots )=\operatorname {M} (\ldots ,\,x_{j},\,\ldots ,\,x_{i},\,\ldots )}$

Monotonie

${\displaystyle a<b\Rightarrow \operatorname {M} (a,x_{1},x_{2},\ldots x_{n})<\operatorname {M} (b,x_{1},x_{2},\ldots x_{n})}$

Idempotence

${\displaystyle \forall x,\;M(x,x,\ldots x)=x}$

La monotonie et l'idempotence combinées impliquent que la moyenne d'un ensemble se situe toujours entre les extrema de l'ensemble :

${\displaystyle \min(x_{1},\,\ldots ,\,x_{n})\leq \operatorname {M} (x_{1},\,\ldots ,\,x_{n})\leq \max(x_{1},\,\ldots ,\,x_{n})}$

Les moyennes harmonique et arithmétique sont duales réciproques l'une de l'autre pour des arguments positifs :

${\displaystyle \operatorname {H} \left({\frac {1}{x_{1}}},\,\ldots ,\,{\frac {1}{x_{n}}}\right)={\frac {1}{\operatorname {A} \left(x_{1},\,\ldots ,\,x_{n}\right)}}}$

tandis que la moyenne géométrique est sa propre duale réciproque :

${\displaystyle \operatorname {G} \left({\frac {1}{x_{1}}},\,\ldots ,\,{\frac {1}{x_{n}}}\right)={\frac {1}{\operatorname {G} \left(x_{1},\,\ldots ,\,x_{n}\right)}}}$

Inégalités entre moyennes

Quand tous les arguments sont positifs, on peut ordonner les différentes moyennes :

${\displaystyle \min \leq \operatorname {H} \leq \operatorname {G} \leq \operatorname {A} \leq \max }$

et l'égalité est atteinte si et seulement si tous les nombres sont égaux.

C'est une généralisation de l'inégalité arithmético-géométrique et un cas spécial d'inégalité entre moyennes de différents ordres.

L'étude des moyennes pythagoriciennes est très proche de l'étude de la majoration et des fonctions Schur-convexes. Les moyennes harmoniques et géométriques sont concaves et symétriques, donc Schur-concaves, tandis que la moyenne arithmétique est multi-linéaire, donc concave et convexe à la fois.

Histoire

L'essentiel de ce qu'on connait des moyennes pythagoriciennes vient des ouvrages arithmétiques du I^er siècle et II^e siècle. Nicomaque de Gérase dit qu'elles étaient « connues de tous les anciens, Pythagore, Platon et Aristote. » La première utilisation vient du philosophe pythagoricien Archytas de Tarente :

« Il y a trois moyennes en musique : l'une est l'arithmétique, la deuxième est la géométrique, la troisième est la sous-contraire, qu'ils appellent harmonique. La moyenne est arithmétique lorsque trois termes sont en proportion telle que l'excès dont le premier dépasse le second est celui dont le second dépasse le troisième. Dans cette proportion il s'avère que l'intervalle des plus grands termes est moindre, mais celui des moindres termes plus grand. La moyenne est la géométrique quand elles sont telles que comme la première est à la seconde, ainsi la seconde est à la troisième. De ces termes, le plus grand et le plus petit ont entre eux un intervalle égal. La sous-contraire, que nous appelons harmonique, est la moyenne quand ils sont tels que, de quelque partie de lui-même que le premier terme dépasse le second, de cette partie du troisième le moyen terme dépasse le troisième. Il s'avère que dans cette proportion l'intervalle entre les termes supérieurs est plus grand et celui entre les termes inférieurs est moindre^[2]. »

Le nom de "moyenne harmonique", selon Jamblique, est utilisé par Archytas et Hippase de Métaponte. Les moyennes pythagoriciennes apparaissent également dans le Timée de Platon. Elles sont aussi citées dans un commentaire de Pappus d'Alexandrie.

« C'est [...] Théétète qui distingue les puissances qui sont commensurables en longueur de celles qui sont incommensurables, et qui divisent les droites irrationnelles les plus connues des différentes moyennes, en associant les médianes à la géométrie, les binomiales à l'arithmétique, et l'apotome à l'harmonie, comme le dit Eudème de Rhodes, le Péripatéticien^[3]. »

Le terme de "moyenne" (μεσότης, mesótēs en grec ancien) apparait dans des ouvrages arithmétiques néopythagoriciens en lien avec le terme de "proportion" (ἀναλογία, analogía en grec ancien).^{[citation nécessaire]}

Curiosité

Les plus petites paires d'entiers naturels telles que leurs moyennes arithmétique, géométrique et harmonique sont aussi entières sont (5,45) et (10,40).

Voir aussi

• Moyenne arithmético-géométrique
• Moyenne
• Nombre d'or
• Triangle de Kepler

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pythagorean means » (voir la liste des auteurs).

Liens externes

• (en) Cantrell, David W., « Pythagorean Means », sur MathWorld

• Portail des mathématiques