Chaîne de Markov

Cet article ne cite pas suffisamment ses sources (mars 2021).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En mathématiques, une chaîne de Markov est un processus de Markov à temps discret, ou à temps continu et à espace d'états discret. Un processus de Markov est un processus stochastique possédant la propriété de Markov : l'information utile pour la prédiction du futur est entièrement contenue dans l'état présent du processus et n'est pas dépendante des états antérieurs (le système n'a pas de « mémoire »). Les processus de Markov portent le nom de leur inventeur, Andreï Markov.

Un processus de Markov à temps discret est une séquence ${\displaystyle X_{0},}$ ${\displaystyle X_{1},}$ ${\displaystyle X_{2},}$ ${\displaystyle X_{3},\ \dots }$ de variables aléatoires à valeurs dans l’espace des états, qu'on notera ${\displaystyle E}$ dans la suite. La valeur ${\displaystyle X_{n}}$ est l'état du processus à l'instant ${\displaystyle n.}$ Les applications où l'espace d'états ${\displaystyle E}$ est fini ou dénombrable sont innombrables : on parle alors de chaîne de Markov ou de chaînes de Markov à espace d'états discret. Les propriétés essentielles des processus de Markov généraux, par exemple les propriétés de récurrence et d'ergodicité, s'énoncent ou se démontrent plus simplement dans le cas des chaînes de Markov à espace d'états discret. Cet article concerne précisément les chaînes de Markov à espace d'états discret.

Andreï Markov a publié les premiers résultats sur les chaînes de Markov à espace d'états fini en 1906. Une généralisation à un espace d'états infini dénombrable a été publiée par Kolmogorov en 1936. Les processus de Markov sont liés au mouvement brownien et à l'hypothèse ergodique, deux sujets de physique statistique qui ont été très importants au début du XX^e siècle.

Propriété de Markov faible

Définitions

C'est la propriété caractéristique d'une chaîne de Markov : la prédiction du futur à partir du présent n'est pas rendue plus précise par des éléments d'information supplémentaires concernant le passé, car toute l'information utile pour la prédiction du futur est contenue dans l'état présent du processus. La propriété de Markov faible possède plusieurs formes équivalentes qui reviennent toutes à constater que la loi conditionnelle de ${\displaystyle X_{n+1}}$ sachant le passé, c'est-à-dire sachant ${\displaystyle \left(X_{k}\right)_{0\leq k\leq n},}$ est une fonction de ${\displaystyle X_{n}}$ seul : ${\displaystyle {\begin{aligned}\forall n\geq 0,\forall (i_{0},\ldots ,i_{n-1},i,j)&\in E^{n+2}\ {\text{tel que}}\ \mathbb {P} {\Big (}X_{0}=i_{0},X_{1}=i_{1},\ldots ,X_{n-1}=i_{n-1},X_{n}=i{\Big )}>0,\\\mathbb {P} {\Big (}X_{n+1}=j&\mid \,X_{0}=i_{0},X_{1}=i_{1},\ldots ,X_{n-1}=i_{n-1},X_{n}=i{\Big )}=\mathbb {P} \left(X_{n+1}=j\mid X_{n}=i\right).\end{aligned}}}$

Une variante courante des chaînes de Markov est la chaîne de Markov homogène, pour laquelle la probabilité de transition est indépendante de ${\displaystyle n}$ : ${\displaystyle \forall n\geq 1,\forall (i,j)\in E^{2},\quad \mathbb {P} (X_{n+1}=j\mid X_{n}=i)=\mathbb {P} (X_{n}=j\mid X_{n-1}=i)}$

Dans la suite de l'article on ne considèrera que des chaînes de Markov homogènes. Pour une application intéressante des chaînes de Markov non homogènes à l'optimisation combinatoire, voir l'article Recuit simulé. Il existe une propriété de Markov forte, liée à la notion de temps d'arrêt : cette propriété de Markov forte est cruciale pour la démonstration de résultats importants (divers critères de récurrence, loi forte des grands nombres pour les chaînes de Markov). Elle est énoncée dans l'article « Propriété de Markov ».

Critère

Probabilités de transition

Définition

La terminologie matrice de transition est la plus utilisée, mais elle n'est appropriée, en toute rigueur, que lorsque, pour un entier ${\displaystyle n\geq 1,}$ ${\displaystyle E=\{1,2,\ldots ,n\}.}$ Lorsque ${\displaystyle E}$ est fini, par exemple de cardinal ${\displaystyle n,}$ on peut toujours numéroter les éléments de ${\displaystyle E}$ arbitrairement de 1 à ${\displaystyle n,}$ ce qui règle le problème, mais imparfaitement, car cette renumérotation est contre-intuitive dans beaucoup d'exemples.

Plutôt que de renuméroter les états à partir de 1, il est donc plus ergonomique dans beaucoup de cas d'accepter des matrices finies ou infinies dont les lignes et colonnes sont « numérotées » à l'aide des éléments de ${\displaystyle E.}$ Le produit de deux telles « matrices », ${\displaystyle A=\left(a_{i,j}\right)_{(i,j)\in E^{2}}}$ et ${\displaystyle B=\left(b_{i,j}\right)_{(i,j)\in E^{2}}}$, est alors défini très naturellement par ${\displaystyle (AB)_{i,j}=\sum _{\ell \in E}a_{i,\ell }b_{\ell ,j},}$ par analogie avec la formule plus classique du produit de deux matrices carrées de taille ${\displaystyle n,}$ ${\displaystyle (AB)_{i,j}=\sum _{k=1}^{n}a_{i,k}b_{k,j}.}$

Propriétés

Lorsqu'on étudie une chaîne de Markov particulière, sa matrice de transition est en général bien définie et fixée tout au long de l'étude, mais la loi initiale peut changer lors de l'étude et les notations doivent refléter la loi initiale considérée sur le moment : si à un moment de l'étude on considère une chaîne de Markov de loi initiale définie par ${\displaystyle \forall i\in E,\quad \mathbb {P} \left(X_{0}=i\right)=\mu _{i}}$, alors les probabilités sont notées ${\displaystyle \mathbb {P} _{\mu }\left(\dots \right)}$ et les espérances sont notées ${\displaystyle \mathbb {E} _{\mu }\left[\dots \right]}$. En particulier, si ${\displaystyle \mathbb {P} \left(X_{0}=j\right)=1}$, on dit que la chaîne de Markov part de ${\displaystyle j}$, les probabilités sont notées ${\displaystyle \mathbb {P} _{j}\left(\dots \right)}$ et les espérances sont notées ${\displaystyle \mathbb {E} _{j}\left[\dots \right]}$.

Puissances de la matrice de transition

Pour ${\displaystyle k\geq 1,}$ la probabilité de transition en ${\displaystyle k}$ pas, ${\displaystyle \mathbb {P} \left(X_{n+k}=j\mid X_{n}=i\right),}$ ne dépend pas de ${\displaystyle n}$ :

Par une simple application de la formule des probabilités totales, on en déduit les lois marginales de la chaîne de Markov.

Classification des états

Pour ${\displaystyle (i,j)\in E^{2}}$, on dit que ${\displaystyle j}$ est accessible à partir de ${\displaystyle i}$ si et seulement s'il existe ${\displaystyle n\geq 0}$ tel que ${\displaystyle \mathbb {P} (X_{n}=j\mid X_{0}=i)>0.}$ On note : ${\displaystyle \{j\leftarrow i\}\quad \Leftrightarrow \quad \left\{\exists n\geq 0{\text{ tel que }}p_{i,j}^{(n)}>0\right\}.}$

On dit que ${\displaystyle i}$ et ${\displaystyle j}$ communiquent si et seulement s'il existe ${\displaystyle (n,m)\in \mathbb {N} ^{2}}$ tels que ${\displaystyle \mathbb {P} (X_{n}=j\mid X_{0}=i)>0}$ et ${\displaystyle \mathbb {P} (X_{m}=i\mid X_{0}=j)>0.}$ On note : ${\displaystyle \{j\leftrightarrow i\}\quad \Leftrightarrow \quad \left\{j\leftarrow i{\text{ et }}i\leftarrow j\right\}.}$

La relation communiquer, notée ${\displaystyle \leftrightarrow ,}$ est une relation d'équivalence. Quand on parle de classe en parlant des états d'une chaîne de Markov, c'est en général aux classes d'équivalence pour la relation ${\displaystyle \leftrightarrow }$ qu'on fait référence. Si tous les états communiquent, la chaîne de Markov est dite irréductible.

La relation être accessible, notée ${\displaystyle \leftarrow ,}$ s'étend aux classes d'équivalence : pour deux classes ${\displaystyle C}$ et ${\displaystyle C^{\prime }}$, on a ${\displaystyle \{C\leftarrow C^{\prime }\}\quad \Leftrightarrow \quad \left\{\exists (i,j)\in C\times C^{\prime },\qquad i\leftarrow j\right\}\quad \Leftrightarrow \quad \left\{\forall (i,j)\in C\times C^{\prime },\qquad i\leftarrow j\right\}.}$

La relation ${\displaystyle \leftarrow }$ est une relation d'ordre entre les classes d'équivalence.

Une classe est dite finale si elle ne conduit à aucune autre, i.e. si la classe est minimale pour la relation ${\displaystyle \leftarrow .}$ Sinon, elle est dite transitoire. L'appartenance à une classe finale ou transitoire a des conséquences sur les propriétés probabilistes d'un état de la chaîne de Markov, en particulier sur son statut d'état récurrent ou d'état transient. Le nombre et la nature des classes finales dicte la structure de l'ensemble des probabilités stationnaires, qui résument de manière précise le comportement asymptotique de la chaîne de Markov, comme on peut le voir à la prochaine section et dans les deux exemples détaillés à la fin de cette page.

Soit ${\displaystyle M_{ij}=\left\{n\geq 1\ |\ p_{i,j}^{(n)}>0\right\}.}$

La période d'un état ${\displaystyle i}$ est le PGCD de l'ensemble ${\displaystyle M_{ii}.}$ Si deux états communiquent, ils ont la même période : on peut donc parler de la période d'une classe d'états. Si la période vaut 1, la classe est dite apériodique. L'apériodicité des états d'une chaîne de Markov conditionne la convergence de la loi de ${\displaystyle X_{n}}$ vers la probabilité stationnaire, voir la page Probabilité stationnaire d'une chaîne de Markov.

La classification des états et leur période se lisent de manière simple sur le graphe de la chaîne de Markov. Toutefois, si tous les éléments de la matrice de transition sont strictement positifs, la chaîne de Markov est irréductible et apériodique : dessiner le graphe de la chaîne de Markov est alors superflu.

Loi stationnaire

Définition

Il peut exister une ou plusieurs mesures ${\displaystyle \pi =(\pi _{i})_{i\in E},}$ sur l'espace d'états ${\displaystyle E,}$ telles que : ${\displaystyle \pi =\pi \,P,}$ ou bien encore ${\displaystyle \forall j\in E,\qquad \pi _{j}=\sum _{i\in E}\pi _{i}\,p_{i,j}.}$

Une telle mesure ${\displaystyle \pi }$ est appelée une mesure stationnaire. Une mesure stationnaire est une fonction propre de la transposée de la matrice de transition, associée à la valeur propre 1. Elle est appelée probabilité stationnaire ou loi stationnaire si elle remplit les conditions supplémentaires :

• ${\displaystyle \forall i\in E,\qquad \pi _{i}\ \geq \ 0,}$
• ${\displaystyle \sum _{i\in E}\pi _{i}\ =\ 1.}$

Le terme « stationnaire » est justifié par la proposition suivante :

Plus généralement, la chaîne de Markov est un processus stationnaire si et seulement si sa loi initiale est une probabilité stationnaire.

Existence et unicité

Dans le cas des chaînes de Markov à espace d'états discret, certaines propriétés du processus déterminent s'il existe ou non une probabilité stationnaire, et si elle est unique ou non :

• une chaîne de Markov est irréductible si tout état est accessible à partir de n'importe quel autre état ;
• un état est récurrent positif si l'espérance du temps de premier retour en cet état, partant de cet état, est finie.

Si une chaîne de Markov possède au moins un état récurrent positif, alors il existe une probabilité stationnaire. S'il existe une probabilité stationnaire ${\displaystyle \pi }$ telle que ${\displaystyle \pi _{i}>0}$, alors l'état ${\displaystyle i}$ est récurrent positif, et réciproquement.

Ce théorème vaut en particulier pour les chaînes de Markov irréductibles, puisque ces dernières possèdent une seule classe (qui est donc nécessairement une classe finale) ; les chaînes de Markov irréductibles vérifient en particulier ${\displaystyle C=E.}$

Loi forte des grands nombres et ergodicité

Dans le cas d'une chaîne de Markov irréductible et récurrente positive, la loi forte des grands nombres est en vigueur : la moyenne d'une fonction ${\displaystyle f}$ sur les instances de la chaîne de Markov est égale à sa moyenne selon sa probabilité stationnaire. Plus précisément, sous l'hypothèse ${\displaystyle \sum _{i\in E}|f(i)|\,\pi _{i}\ <+\infty ,}$ on a presque sûrement : ${\displaystyle \lim _{n}\;{\frac {1}{n}}\;\sum _{k=0}^{n-1}f(X_{k})\ =\ \sum _{i\in E}f(i)\,\pi _{i}\ =\ \pi f.}$

La moyenne de la valeur des instances est donc, sur le long terme, égale à l'espérance suivant la probabilité stationnaire. En particulier, cette équivalence sur les moyennes s'applique si ${\displaystyle f}$ est la fonction indicatrice d'un sous-ensemble ${\displaystyle A}$ de l'espace des états : ${\displaystyle \lim _{n}\;{\frac {1}{n}}\;\sum _{k=0}^{n-1}\chi _{A}(X_{k})\ =\ \sum _{i\in A}\ \pi _{i}\ =\ \pi (A).}$

Cela permet d'approcher la probabilité stationnaire par la distribution empirique (qui est un histogramme construit à partir d'une séquence particulière), comme dans le cas de la marche aléatoire avec barrière.

En particulier, si le processus est construit en prenant la probabilité stationnaire comme loi initiale, le shift ${\displaystyle \theta }$ défini par ${\displaystyle x=(x_{0},x_{1},x_{2},\dots )\in E^{\mathbb {N} }\quad \rightarrow \quad \theta \,x=(x_{1},x_{2},x_{3},\dots )}$ préserve la mesure, ce qui fait de la chaîne de Markov un système dynamique mesuré. La loi forte des grands nombres entraine alors que la chaîne de Markov est un système dynamique ergodique. L'ergodicité est à la fois plus forte que la loi forte des grands nombres car on peut en déduire, par exemple, que ${\displaystyle {\frac {1}{n}}\;\sum _{k=0}^{n-1}f(X_{k},X_{k+1}),}$ a pour limite presque sûre ${\displaystyle \sum _{i,j\in E}f(i,j)\,\pi _{i}p_{i,j},}$ mais elle est aussi plus faible car elle réclame en principe la stationnarité de la chaîne de Markov, ce qui n'est pas le cas de la loi forte des grands nombres.

Convergence vers la loi stationnaire

Si la chaîne de Markov est irréductible, récurrente positive et apériodique, alors ${\displaystyle P^{k}}$ converge vers une matrice dont chaque ligne est l'unique distribution stationnaire ${\displaystyle \pi .}$ En particulier, la loi ${\displaystyle \mu _{n}}$ de ${\displaystyle X_{n}}$ converge vers ${\displaystyle \pi }$ indépendamment de la loi initiale ${\displaystyle \mu _{0}.}$ Dans le cas d'un espace d'état fini, cela se prouve par le théorème de Perron-Frobenius. Notons qu'il est naturel que la suite ${\displaystyle \mu _{n},}$ définie par récurrence par la relation ${\displaystyle \mu _{n+1}=\mu _{n}P,}$ ait, éventuellement, pour limite un point fixe de cette transformation, i.e. une solution de l'équation ${\displaystyle \pi =\pi P.}$

Chaînes de Markov à espace d'états fini

Si une chaîne de Markov est irréductible et si son espace d'états est fini, tous ses états sont récurrents positifs. La loi forte des grands nombres est alors en vigueur.

Plus généralement, tous les éléments d'une classe finale finie sont récurrents positifs, que l'espace d'états soit fini ou bien infini dénombrable.

Distributions quasi-stationnaires d'une chaîne de Markov absorbée

Soit ${\displaystyle (X_{n})}$ une chaîne de Markov sur l'ensemble des entiers naturels ${\displaystyle \{0,1,2,...\}}$. Supposons que l'état 0 soit absorbant et la chaîne soit absorbée en 0 presque sûrement. Soit ${\displaystyle T_{0}=\inf\{n\geq 0,X_{n}=0\}}$ le temps d'absorption en 0. On dit qu'une probabilité ${\displaystyle \nu }$ sur ${\displaystyle \{1,2,3,...\}}$ est une distribution quasi-stationnaire si pour tout ${\displaystyle j\geq 1}$ et pour tout ${\displaystyle n\geq 1}$,

${\displaystyle \sum _{i\geq 1}\nu _{i}\mathbb {P} (X_{n}=j|X_{0}=i,T_{0}>n)=\nu _{j}.}$

On dit qu'une probabilité ${\displaystyle \mu }$ sur ${\displaystyle \{1,2,3,...\}}$ est une limite de Yaglom si pour tout ${\displaystyle i\geq 1}$ et tout ${\displaystyle j\geq 1}$,

${\displaystyle \lim _{n\to \infty }\mathbb {P} (X_{n}=j|X_{0}=i,T_{0}>n)=\mu _{j}.}$

Une limite de Yaglom est une distribution quasi-stationnaire. Si elle existe, la limite de Yaglom est unique. En revanche, il peut y avoir plusieurs distributions quasi-stationnaires.

Si ${\displaystyle \nu }$ est une distribution quasi-stationnaire, alors il existe un nombre réel ${\displaystyle \rho (\nu )\in ]0,1[}$ tel que ${\displaystyle \sum _{i}\nu _{i}\mathbb {P} (T_{0}>n|X_{0}=i)=\rho (\nu )^{n}}$.

Notation

Dans les formules qui précèdent, l'élément (${\displaystyle i,j}$) est la probabilité de la transition de ${\displaystyle i}$ à ${\displaystyle j}$. La somme des éléments d'une ligne vaut toujours 1 et la distribution stationnaire est donnée par le vecteur propre gauche de la matrice de transition.

On rencontre parfois des matrices de transition dans lesquelles le terme (${\displaystyle i,j}$) est la probabilité de transition de ${\displaystyle j}$ vers ${\displaystyle i}$, auquel cas la matrice de transition est simplement la transposée de celle décrite ici. La somme des éléments d'une colonne vaut alors 1. De plus, la distribution stationnaire du système est alors donnée par le vecteur propre droit de la matrice de transition, au lieu du vecteur propre gauche.

Exemple : Doudou le hamster

Doudou le hamster ne connaît que trois endroits dans sa cage : les copeaux où il dort, la mangeoire où il mange et la roue où il fait de l'exercice. Ses journées sont assez semblables les unes aux autres, et son activité se représente aisément par une chaîne de Markov. Toutes les minutes, il peut soit changer d'activité, soit continuer celle qu'il était en train de faire. L'appellation processus sans mémoire n'est pas du tout exagérée pour parler de Doudou.

• Quand il dort, il a 9 chances sur 10 de ne pas se réveiller la minute suivante.
• Quand il se réveille, il y a 1 chance sur 2 qu'il aille manger et 1 chance sur 2 qu'il parte faire de l'exercice.
• Le repas ne dure qu'une minute, après il fait autre chose.
• Après avoir mangé, il y a 3 chances sur 10 qu'il parte courir dans sa roue, mais surtout 7 chances sur 10 qu'il retourne dormir.
• Courir est fatigant pour Doudou ; il y a 8 chances sur 10 qu'il retourne dormir au bout d'une minute. Sinon il continue en oubliant qu'il est déjà un peu fatigué.

Diagrammes

Les diagrammes peuvent montrer toutes les flèches, chacune représentant une probabilité de transition. Cependant, c'est plus lisible si :

• on ne dessine pas les flèches de probabilité zéro (transition impossible) ;
• on ne dessine pas les boucles (flèche d'un état vers lui-même). Cependant elles existent ; leur probabilité est sous-entendue car on sait que la somme des probabilités des flèches partant de chaque état doit être égale à 1.

• 
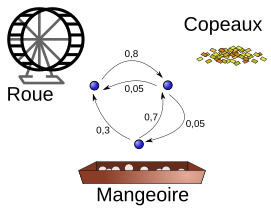  Exemple avec boucles implicites
• 
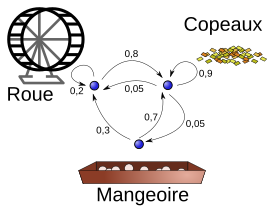  Exemple avec boucles dessinées

Matrice de transition

La matrice de transition de ce système est la suivante (les lignes et les colonnes correspondent dans l'ordre aux états représentés sur le graphe par copeaux, mangeoire, roue) : ${\displaystyle P={\begin{bmatrix}0,9&0,05&0,05\\0,7&0&0,3\\0,8&0&0,2\\\end{bmatrix}}}$

Prévisions

Prenons l'hypothèse que Doudou dort lors de la première minute de l'étude. ${\displaystyle \mathbf {x} ^{(0)}={\begin{bmatrix}1&0&0\end{bmatrix}}}$

Au bout d'une minute, on peut prédire : ${\displaystyle \mathbf {x} ^{(1)}=\mathbf {x} ^{(0)}P={\begin{bmatrix}1&0&0\end{bmatrix}}{\begin{bmatrix}0,9&0,05&0,05\\0,7&0&0,3\\0,8&0&0,2\\\end{bmatrix}}={\begin{bmatrix}0,9&0,05&0,05\end{bmatrix}}}$

Ainsi, après une minute, on a 90 % de chances que Doudou dorme encore, 5 % qu'il mange et 5 % qu'il coure.

${\displaystyle \mathbf {x} ^{(2)}=\mathbf {x} ^{(1)}P=\mathbf {x} ^{(0)}P^{2}={\begin{bmatrix}1&0&0\end{bmatrix}}{\begin{bmatrix}0,9&0,05&0,05\\0,7&0&0,3\\0,8&0&0,2\\\end{bmatrix}}^{2}={\begin{bmatrix}0,885&0,045&0,07\end{bmatrix}}}$

Après 2 minutes, il y a 4,5 % de chances que le hamster mange.

De manière générale, pour ${\displaystyle n}$ minutes : ${\displaystyle \mathbf {x} ^{(n)}=\mathbf {x} ^{(n-1)}P}$ et ${\displaystyle \mathbf {x} ^{(n)}=\mathbf {x} ^{(0)}P^{n}}$

La théorie montre qu'au bout d'un certain temps, la loi de probabilité est indépendante de la loi initiale. Notons-la ${\displaystyle q}$ : ${\displaystyle \mathbf {q} =\lim _{n\to \infty }\mathbf {x} ^{(n)}}$

On obtient la convergence si et seulement si la chaîne est apériodique et irréductible. C'est le cas dans notre exemple, on peut donc écrire : ${\displaystyle {\begin{aligned}\\&\mathbf {q} =\mathbf {q} P\qquad {\mbox{(}}\mathbf {q} {\mbox{ est la loi invariante par rapport à }}P{\mbox{ avec }}P={\begin{bmatrix}0,9&0,05&0,05\\0,7&0&0,3\\0,8&0&0,2\\\end{bmatrix}}{\mbox{.)}}\\\iff &\mathbf {q} -\mathbf {q} P={\begin{bmatrix}0&0&0\end{bmatrix}}\\\iff &\mathbf {q} (I-P)={\begin{bmatrix}0&0&0\end{bmatrix}}\\\iff &\mathbf {q} \left({\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}}-{\begin{bmatrix}0,9&0,05&0,05\\0,7&0&0,3\\0,8&0&0,2\\\end{bmatrix}}\right)={\begin{bmatrix}0&0&0\end{bmatrix}}\\\iff &\mathbf {q} {\begin{bmatrix}0,1&-0,05&-0,05\\-0,7&1&-0,3\\-0,8&0&0,8\\\end{bmatrix}}={\begin{bmatrix}0&0&0\end{bmatrix}}\\\iff &{\begin{bmatrix}q_{1}&q_{2}&q_{3}\end{bmatrix}}{\begin{bmatrix}0,1&-0,05&-0,05\\-0,7&1&-0,3\\-0,8&0&0,8\\\end{bmatrix}}={\begin{bmatrix}0&0&0\end{bmatrix}}\end{aligned}}}$

Sachant que ${\displaystyle q_{1}+q_{2}+q_{3}=1}$, on obtient : ${\displaystyle {\begin{bmatrix}q_{1}&q_{2}&q_{3}\end{bmatrix}}={\begin{bmatrix}0,884&0,0442&0,0718\end{bmatrix}}}$

Doudou passe donc 88,4 % de son temps à dormir, 4,42 % à manger et 7,18 % à courir.

Illustration de l'impact du modèle

L'exemple qui suit a pour but de montrer l'importance de la modélisation du système. Une bonne modélisation permet de répondre à des questions complexes avec des calculs simples.

On étudie une civilisation (fictive) constituée de plusieurs classes sociales, et dans laquelle les individus peuvent passer d'une classe à l'autre. Chaque étape représentera un an. On considérera une lignée plutôt qu'un individu, pour éviter d'obtenir des citoyens bicentenaires. Les différents statuts sociaux sont au nombre de quatre :

• esclave ;
• libre ;
• citoyen ;
• haut fonctionnaire.

Dans cette société :

• les esclaves peuvent rester esclaves ou devenir des hommes libres (en achetant leur liberté ou en étant affranchis généreusement par leur maître) ;
• les hommes libres peuvent rester libres ou bien vendre leur liberté (pour payer leurs dettes, etc.) ou encore devenir citoyens (là encore par mérite ou en achetant le titre de citoyen) ;
• les citoyens sont citoyens à vie et transmettent leur citoyenneté à leur lignée (on pourrait croire que le nombre de citoyens tend à augmenter et qu'au bout d'un certain temps, tous sont citoyens mais historiquement, dans les civilisations qui suivaient ce schéma, les citoyens sont décimés par les guerres et de nouveaux esclaves arrivent régulièrement de l'étranger). Ils peuvent aussi se porter candidats lors des élections annuelles afin de devenir hauts-fonctionnaires (magistrats). Au terme de leur mandat, ils peuvent être réélus ou redevenir de simples citoyens.

Pour compliquer un peu l'exemple et montrer ainsi l'étendue des applications des chaînes de Markov, nous considérerons que les fonctionnaires sont élus pour plusieurs années. Par conséquent, l'avenir d'un individu fonctionnaire dépend du temps depuis lequel il est fonctionnaire. Nous sommes donc dans le cas d'une chaîne de Markov non homogène. Heureusement, nous pouvons aisément nous ramener à une chaîne homogène. En effet, il suffit de rajouter un état artificiel pour chaque année du mandat. Au lieu d'avoir un état 4 : Fonctionnaire, nous aurons un état :

• 4 : Fonctionnaire en début de mandat ;
• 5 : Fonctionnaire en seconde année de mandat ;
• etc.

Les probabilités reliant deux états artificiels consécutifs (troisième et quatrième année par exemple) sont de valeur 1 car l'on considère que tout mandat commencé se termine (on pourrait modéliser le contraire en changeant la valeur de ces probabilités). Fixons la durée des mandats à deux ans, le contingent des fonctionnaires étant renouvelable par moitié chaque année. On a alors le graphe suivant :

Pour modéliser des élections qui ne seraient pas annuelles, il faudrait de même ajouter des états fictifs (année d'élection, un an depuis la dernière élection, etc.).

La matrice ${\displaystyle P}$ s'écrit alors : ${\displaystyle \mathbf {P} ={\begin{bmatrix}{\frac {97}{98}}&{\frac {1}{98}}&0&0&0\\{\frac {2}{73}}&{\frac {65}{73}}&{\frac {6}{73}}&0&0\\0&0&{\frac {12}{13}}&{\frac {1}{13}}&0\\0&0&0&0&1\\0&0&{\frac {7}{8}}&{\frac {1}{8}}&0\end{bmatrix}}}$

Comme cela est expliqué plus haut, ${\displaystyle P^{n}}$ donne les probabilités de transition en ${\displaystyle n}$ étapes. Donc ${\displaystyle p_{ij}^{n}}$ est la probabilité d'être dans l'état ${\displaystyle j}$ au bout de ${\displaystyle n}$ années pour une lignée partie de la classe sociale ${\displaystyle i}$. Pour savoir ce que devient un esclave au bout de ${\displaystyle n}$ ans, il suffit donc d'écrire : ${\displaystyle {\begin{bmatrix}1&0&0&0&0\end{bmatrix}}\times \mathbf {P} ^{(n)}={\begin{bmatrix}p_{1}^{(n)}&p_{2}^{(n)}&p_{3}^{(n)}&p_{4}^{(n)}&p_{5}^{(n)}\end{bmatrix}}}$

Où ${\displaystyle p_{i}^{n}}$ est la probabilité d'être dans la classe sociale ${\displaystyle i}$ au bout de ${\displaystyle n}$ années sachant que la lignée étudiée est partie de l'état d'esclave.

Si on connaît les effectifs de chaque classe sociale à l'an 0, il suffit alors de calculer : ${\displaystyle {\frac {1}{\mathrm {lign{\acute {e}}es} }}\times {\begin{bmatrix}{\rm {esclaves}}&{\rm {libres}}&{\rm {citoyens}}&{\rm {{\acute {e}}lus_{1}}}&{\rm {{\acute {e}}lus_{2}}}\end{bmatrix}}\times \mathbf {P} ^{n}=Y}$

On obtient ainsi la répartition de la population dans les différentes classes sociales (au bout de ${\displaystyle n}$ années). En multipliant ce vecteur ${\displaystyle Y}$ par l'effectif total de la population, on obtient les effectifs de chaque classe au bout de ${\displaystyle n}$ années.

Posons-nous maintenant la question suivante : « Au bout de ${\displaystyle n}$ années, combien de lignées auront déjà eu un haut fonctionnaire ayant terminé son mandat ? »

La réponse est différente du nombre de mandats effectués en ${\displaystyle n}$ années car il y a possibilité d'être réélu. Répondre à cette question semble difficile (encore faudrait-il que ce soit possible). En fait, il suffit de changer la modélisation du problème. Passons donc à une nouvelle modélisation pour répondre à cette question. (Par contre, elle ne permet pas de répondre aux questions précédentes d'où la présentation des deux modèles.)

Il suffit de modifier ainsi le graphe :

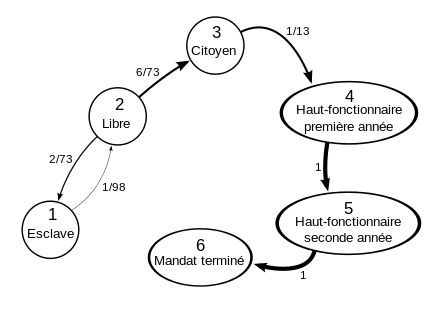
On ajoute un sommet absorbant car une fois qu'une lignée a fini un mandat, on ne tient plus compte d'elle.

Si certains lecteurs font preuve d'esprit critique, ils diront peut-être que le modèle est faux car les lignées comportant un élu ne participent plus aux élections. Il n'en est rien. En effet, le nombre d'élus est proportionnel au nombre de citoyens. Ne pas réinjecter les anciens hauts-fonctionnaires parmi les candidats ne change donc en rien la probabilité pour un citoyen d'être élu car, la population des citoyens étant plus restreinte, le nombre de postes offerts l'est aussi. Ce modèle permet de répondre avec exactitude à la question posée.

On a donc une nouvelle matrice de transition : ${\displaystyle \mathbf {Q} ={\begin{bmatrix}{\frac {97}{98}}&{\frac {1}{98}}&0&0&0&0\\{\frac {2}{73}}&{\frac {65}{73}}&{\frac {6}{73}}&0&0&0\\0&0&{\frac {12}{13}}&{\frac {1}{13}}&0&0\\0&0&0&0&1&0\\0&0&0&0&0&1\\0&0&0&0&0&1\end{bmatrix}}}$

En faisant les mêmes calculs qu'aux questions précédentes on obtient en dernière ligne du vecteur solution le pourcentage de lignées ayant accompli au moins un mandat ou bien l'effectif (si on multiplie par l'effectif total de la population). Autrement dit, modéliser à nouveau le problème permet de répondre à la question qui semblait si compliquée par un simple calcul de puissances d'une matrice.

Applications

Cette section ne cite pas suffisamment ses sources (mars 2017). 

Pour l'améliorer, ajoutez des références de qualité et vérifiables (comment faire ?) ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

• Un processus de Bernoulli est un exemple simple de chaîne de Markov.
• Les systèmes markoviens sont très présents en physique particulièrement en physique statistique. Plus généralement l'hypothèse markovienne est souvent invoquée lorsque des probabilités sont utilisées pour modéliser l'état d'un système, en supposant toutefois que l'état futur du système peut être déduit du passé avec un historique assez faible.
• Le célèbre article de 1948 de Claude Shannon, A mathematical theory of communication, qui fonde la théorie de l'information, commence en introduisant la notion d'entropie à partir d'une modélisation markovienne de la langue anglaise. Il montre ainsi le degré de prédictibilité de la langue anglaise, muni d'un simple modèle d'ordre 1. Bien que simples, de tels modèles permettent de bien représenter les propriétés statistiques des systèmes et de réaliser des prédictions efficaces sans décrire la structure complète des systèmes.
• En compression, la modélisation markovienne permet la réalisation de techniques de codage entropique très efficaces, comme le codage arithmétique. De très nombreux algorithmes en reconnaissance des formes ou en intelligence artificielle comme l'algorithme de Viterbi, utilisé dans la grande majorité des systèmes de téléphonie mobile pour la correction d'erreurs, font l'hypothèse d'un processus markovien sous-jacent.
• L'indice de popularité d'une page Web (PageRank) tel qu'il est utilisé par Google est défini par une chaîne de Markov. Il est défini par la probabilité d'être dans cette page à partir d'un état quelconque de la chaine de Markov représentant le Web. Si ${\displaystyle N}$ est le nombre de pages Web connues, et une page ${\displaystyle i}$ a ${\displaystyle k_{i}}$ liens, alors sa probabilité de transition vers une page liée (vers laquelle elle pointe) est ${\displaystyle p_{i}^{l}={\tfrac {1-q}{k_{i}}}+{\tfrac {q}{N}}}$ et ${\displaystyle p_{i}^{nl}={\tfrac {q}{N}}}$ pour toutes les autres (pages non liées). Notons qu'on a bien ${\displaystyle k_{i}p_{i}^{l}+(N-k_{i})p_{i}^{nl}=1}$. Le paramètre ${\displaystyle q}$ vaut environ 0,15.
• Les chaînes de Markov sont un outil fondamental pour modéliser les processus en théorie des files d'attente et en statistiques.
• Les chaînes de Markov sont couramment employées en sûreté de fonctionnement pour les calculs de fiabilité et de disponibilité des systèmes techniques, en particulier pour modéliser des séquences d'évènements de type pannes, réparations, changements de configuration.
• Les chaînes de Markov fondent les systèmes de Bonus/Malus mis au point par les actuaires des sociétés d'assurances automobiles (la probabilité d'avoir n accidents au cours de l'année t étant conditionnée par le nombre d'accidents en t-1)
• Les chaînes de Markov sont également utilisées en bioinformatique pour modéliser les relations entre symboles successifs d'une même séquence (de nucléotides par exemple), en allant au-delà du modèle polynomial. Les modèles markoviens cachés ont également diverses utilisations, telles que la segmentation (définition de frontières de régions au sein de séquences de gènes ou de protéines dont les propriétés chimiques varient), l'alignement multiple, la prédiction de fonction, ou la découverte de gènes (les modèles markoviens cachés sont plus « flexibles » que les définitions strictes de type codon start + multiples codons + codons stop et ils sont donc plus adaptés pour les eucaryotes (à cause de la présence d'introns dans le génome de ceux-ci) ou pour la découverte de pseudo-gènes).
• On peut se servir de ce type de chaines pour produire des mots, du texte, pour suggérer un mot à écrire^[1].

Notes et références

Voir aussi

Articles connexes

• Méthode de Monte-Carlo par chaînes de Markov
• Matrice d'adjacence
• Problème de décision de Markov (MDP)
• Problème de décision de Markov partiellement observable (POMDP)
• Marche aléatoire
• Mouvement brownien
• Modèle des urnes d'Ehrenfest
• Modèle de Markov caché
• Processus de Markov à temps continu
• Processus de Markov
• Propriété de Markov
• Couverture de Markov
• Martingale
• Équation maîtresse

Bibliographie

• Bruno Sericola : Chaînes de Markov - Théorie, algorithmes et applications. Hermes/Lavoisier, 2013.
• Sylvie Méléard : Modèles aléatoires en écologie et évolution. Springer, 2016.
• Paolo Baldi, Laurent Mazliak, Pierre Priouret, Martingales et chaînes de Markov. Théorie élémentaire et exercices corrigés, (ISBN 2-7056-6425-4), Hermann (éditions), 2001

Liens externes

• Philippe Gay, « Markov et la Belle au bois dormant », sur Images des Maths, 5 septembre 2014
• (en) [PDF] Charles M. Grinstead et J. Laurie Snell, chap. « Markov Chains », dans Introduction to probability, AMS
• (en) Markov Marvellous Chain
• Exercices corrigés (wims de l'université de Nice Sophia Antipolis)

• Portail des probabilités et de la statistique
• Portail de la physique