Rozkład Poissona
Funkcja rozkładu prawdopodobieństwa Na osi poziomej jest indeks Funkcja jest zdefiniowana tylko dla całkowitych wartości Linie łączące te punkty są jedynie konwencją wykresu i nie oznaczają ciągłości. | |
Dystrybuanta Na osi poziomej jest indeks | |
| Parametry |
|
|---|---|
| Nośnik |
|
| Funkcja rozkładu prawdopodobieństwa |
|
| Dystrybuanta | (gdzie to niekompletna funkcja gamma) |
| Wartość oczekiwana (średnia) |
|
| Mediana |
|
| Moda | i gdzie jest całkowite |
| Wariancja |
|
| Współczynnik skośności |
|
| Kurtoza |
|
| Entropia | |
| Funkcja tworząca momenty |
|
| Funkcja charakterystyczna |
|
| Odkrywca | Siméon Denis Poisson |
Rozkład Poissona (czytaj [pwasɔ̃], także prawo Poissona małych liczb[1]) – dyskretny rozkład prawdopodobieństwa, wyrażający prawdopodobieństwo szeregu wydarzeń mających miejsce w określonym czasie, gdy te wydarzenia występują ze znaną średnią częstotliwością i w sposób niezależny od czasu jaki upłynął od ostatniego zajścia takiego zdarzenia. Rozkład Poissona można również stosować w odniesieniu do liczby zdarzeń w innych określonych przedziałach, takich jak odległość, powierzchnia lub objętość.
Rozkład został wprowadzony i opublikowany przez Siméona-Denisa Poissona (1781–1840) wraz z jego teorią prawdopodobieństwa, w 1838 roku w jego pracy Recherches sur la probabilité des jugements en matière criminelle et en matière civile („Badania nad prawdopodobieństwem orzeczeń sądowych w sprawach cywilnych i karnych”). Praca skupiała się na niektórych zmiennych losowych wyrażających, między innymi, liczbę dyskretnych zdarzeń, które odbywają się w przedziale czasu, o określonej długości.
Jeśli oczekiwaną liczbą zdarzeń w tym przedziale jest to prawdopodobieństwo, że jest dokładnie wystąpień, gdzie jest nieujemną liczbą całkowitą, jest równe
gdzie:
- – podstawa logarytmu naturalnego
- – liczba wystąpień zdarzenia, prawdopodobieństwo dane funkcją,
- – silnia
- – dodatnia liczba rzeczywista, równa oczekiwanej liczbie zdarzeń w danym przedziale czasu. Na przykład jeżeli zdarzenia występują średnio 4 razy na minutę, a ktoś jest zainteresowany prawdopodobieństwem zdarzenia razy występującego w 10 minut, może użyć rozkładu Poissona jako model z
Jako funkcja jest to funkcja masy prawdopodobieństwa. Rozkład Poissona można wyprowadzić jako graniczny przypadek rozkładu dwumianowego.
Rozkład Poissona może być stosowany do systemów z dużą liczbą możliwych zdarzeń, z których każde jest bardzo rzadkie. Klasycznym przykładem jest rozpad jąder atomowych.
Rozkład Poissona jest czasami nazywany „poissonianem”.
Charakterystyka szumu Poissona i małych zdarzeń
Parametr jest nie tylko średnią liczbą wystąpień ale także ich wariancją (patrz tabela). Tym samym liczba zaobserwowanych zdarzeń oscyluje wokół średniej z odchyleniem standardowym Wahania te są oznaczone jako szum Poissona lub (zwłaszcza w elektronice) jako szum śrutowy.
Korelacja średniej i odchylenie standardowe w liczeniu niezależnych zdarzeń dyskretnych jest przydatna naukowo. Dzięki monitorowaniu jak wahania różnią się od średniej sygnału, można oszacować wkład jednego zdarzenia, nawet jeśli ten wkład jest zbyt mały do wykrycia bezpośrednio. Na przykład ładunek e elektronu może być określony poprzez skorelowanie wielkości prądu elektrycznego z jego szumem śrutowym. Jeżeli przez punkt przechodzi w czasie średnio elektronów, średni prąd jest równy ponieważ wahania prądu powinny być rzędu (tj. standardowe odchylenie procesu Poissona), ładunek może być oszacowany ze współczynnika Codziennym przykładem jest ziarnistość, która pojawia się przy powiększeniach fotografii, ziarnistość ta pojawia się w związku z wahaniami Poissona w ograniczonej liczbie ziaren srebra, a nie w związku z pojedynczymi ziarnami. Korelując ziarnistość ze stopniem powiększenia, można oszacować udział indywidualnych ziaren (które są zbyt małe, aby je inaczej postrzegać samodzielnie). Opracowano wiele innych zastosowań molekularnych szumu Poissona, np. szacowanie gęstości liczby cząsteczek receptora w błonie komórkowej
Rozkłady powiązane
- Jeśli i to różnica ma rozkład Skellama.
- Jeśli i są niezależne, a to rozkład pod warunkiem jest dwumianowy. W szczególności, Ogólnie rzecz biorąc, jeśli są niezależnymi zmiennymi losowymi Poissona z parametrami wtedy
- Rozkład Poissona może zostać wyprowadzony jako graniczny przypadek rozkładu dwumianowego gdy liczba prób dąży do nieskończoności a oczekiwana liczba sukcesów jest stała – patrz prawo rzadkich zdarzeń poniżej. Może być on zatem stosowany jako przybliżenie rozkład dwumianowego gdy liczba jest wystarczająco duża i jest dostatecznie małe. Istnieje praktyczna reguła, stwierdzająca, że rozkład Poissona jest dobrym przybliżeniem rozkładu dwumianowego, jeśli jest co najmniej 20 i jest mniejsza lub równa 0,05, oraz bardzo dobrym przybliżeniem, jeśli i [2].
- Dla dostatecznie dużych wartości (powiedzmy ), rozkład normalny ze średnią i wariancją (odchylenie standardowe ), jest znakomitym przybliżeniem rozkładu Poissona. Jeśli jest większe niż około 10 wtedy rozkład normalny jest dobrym przybliżeniem, jeżeli są wykonywane odpowiednie korekty ciągłości, tj. gdzie (małą literą) jest liczbą całkowitą nieujemną, otrzymuje
- Transformacja stabilizująca wariancję: gdy zmienna ma rozkład Poissona, jej pierwiastek kwadratowy ma w przybliżeniu rozkład normalny z wartością oczekiwaną około i wariancją około 1/4[3]. W ramach tej transformacji, zbieżność do normalności jest znacznie szybsza niż zmiennej przed transformacją. Są dostępne inne, nieco bardziej skomplikowane transformacje stabilizujące wariancję[4] z których jedna jest transformacja Anscombe'a. Zobacz transformacja danych (statystyka) do bardziej ogólnego zastosowania przekształceń.
- Jeśli liczba zajść zdarzenia w danym przedziale czasu jest zgodna z rozkładem Poissona, ze średnią wtedy długość okresu oczekiwania pomiędzy zajściami zdarzenia ma rozkład wykładniczy ze średnią
Występowanie
Rozkład Poissona powstaje w związku z procesami Poissona. Ma on zastosowanie do różnych zjawisk dyskretnych właściwości (czyli tych, które mogą się zdarzyć razy w danym przedziale czasu lub w danym obszarze), gdy prawdopodobieństwo wystąpienia zjawiska jest stałe w czasie lub przestrzeni. Przykłady zdarzeń, które mogą być modelowane rozkładem Poissona to:
- Liczba zabitych przez kopnięcie konia każdego roku w korpusie kawalerii w Prusach. Ten przykład zasłynął z książki Władysława Józefowicza Bortkiewicza (1868–1931).
- Liczba połączeń telefonów przychodzących do centrali na minutę.
- Przy założeniu jednorodności, ile razy serwer jest dostępny na minutę.
- Liczba mutacji w danym odcinku DNA po ekspozycji na pewną dawkę promieniowania.
- Odsetek komórek, które zostaną zakażone dla danej liczności zakażeń.
W jaki sposób powstają takie rozkłady? – Prawo rzadkich zdarzeń
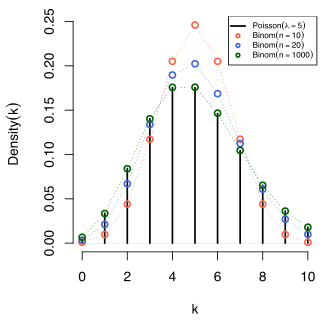
W kilku z powyższych przykładów – takich jak liczba mutacji w danej sekwencji DNA – zdarzenia które są liczone są w wynikami pojedynczych prób, a dokładniej są modelowane przy użyciu rozkładu dwumianowego, to jest
W takich przypadkach jest bardzo duże, a jest bardzo małe (i tak oczekiwane jest pośrednich rozmiarów). Rozkład może być wtedy przybliżany przez mniej uciążliwy rachunkowo rozkład Poissona
To jest znane jako prawo rzadkich zdarzeń, gdyż każde z poszczególnych zdarzeń Bernoulliego rzadko występuje. Nazwa może być myląca, ponieważ całkowita liczba zajścia sukcesu w procesie Poissona nie musi być mała, jeśli parametr nie jest mały. Na przykład liczba telefonów do zajętej centrali w ciągu jednej godziny stosuje się do rozkładu Poissona ze zdarzeniami pojawiającymi się często u operatora, ale są one rzadkie z punktu widzenia przeciętnego członka społeczeństwa, u którego jest bardzo mało prawdopodobne, by dzwonił do centrali w tej godzinie.
Dowód
Będziemy dowodzić, że dla stałych jeśli
to dla każdego ustalonego k
Aby zobaczyć związek z powyższym uzasadnieniem, dla każdej zmiennej losowej o rozkładzie dwumianowym z dużych i małych ustalmy Należy zauważyć, że wartość oczekiwania jest stała względem
Po pierwsze, przypomnijmy, że
wtedy ponieważ w tym przypadku mamy
Dalej, należy pamiętać, że
gdzie rozpatrujemy granicę każdego z członów niezależnie, co można zrobić, ponieważ liczba członów zależnych od jest stała (jest ich ). W związku z tym, musimy wykazać, że
Uogólnienie
Wykazaliśmy, że jeżeli
gdzie a następnie w rozkładzie. Odnosi się to w bardziej ogólnej sytuacji, że jest dowolny ciąg taki, że
2-wymiarowy proces Poissona
 Osobny artykuł: Proces Poissona.
Osobny artykuł: Proces Poissona.
gdzie:
- – podstawa logarytmu naturalnego
- – liczba wystąpień zdarzenia – prawdopodobieństwo, dane funkcją,
- – silnia
- – 2-wymiarowy obszar,
- – pole obszaru,
- – liczba punktów w procesie rozwoju w obszarze.
Własności
- Wartość oczekiwana rozkładu Poissona zmiennej losowej jest równa i jest też ona równa jego wariancji. Wyższe momenty rozkładu Poissona są wielomianami Toucharda z parametrem których współczynniki mają kombinatoryczne znaczenie. W rzeczywistości, gdy wartość oczekiwana rozkładu Poissona jest 1, to wzór Dobińskiego mówi, że -ty moment jest równy liczbie podziałów zbioru -elementowego.
- Dominanta zmiennej losowej o rozkładzie Poissona z niecałkowitą jest równa która jest największą liczbę całkowitą mniejszą lub równą To jest również zapisane jako podłoga Gdy jest liczbą całkowitą, mody są równe i
- Sumy zmiennych losowych o rozkładach Poissona:
- Jeśli mają rozkład Poissona z parametrem i są niezależne, to
- również ma rozkład Poissona o parametrze będącym sumą parametrów składowych. Odwrotne jest twierdzenie Rajkowa, które mówi, że jeśli suma dwóch niezależnych zmiennych losowych ma rozkład Poissona, to ma go również każda z tych dwóch niezależnych zmiennych losowych.
- Suma znormalizowanych odchyleń kwadratowych ma w przybliżeniu rozkład chi kwadrat, jeśli średnia jest umiarkowanej wielkości (zalecana jest )[5]. Jeśli są obserwacjami z niezależnych rozkładów Poissona ze średnimi wtedy
- Funkcją generującą momenty rozkładu Poissona z oczekiwaną wartość jest
- Wszystkie kumulanty rozkładu Poissona są równe wartości oczekiwanej -ty moment silni rozkładu Poissona jest równy
- Rozkład Poissona jest nieskończenie podzielnym rozkładem prawdopodobieństwa.
- Bezpośrednia dywergencja Kullbacka-Leiblera pomiędzy POI i POI jest dana przez
- Wartość oczekiwana policzona z definicji:
Ocena rozkładu Poissona
Chociaż rozkład Poissona jest ograniczony przez licznik i mianownik może osiągnąć skrajne wartości dla dużych wartości lub
Jeżeli rozkład Poissona jest szacowany na komputerze z ograniczoną dokładnością, najpierw wyliczając jego licznik i mianownik, a następnie dzieląc je, to może wystąpić znaczna utrata precyzji.
Na przykład dla typowej podwójnej precyzji zdarzy się całkowita utrata dokładności jeśli jest obliczana w ten sposób.
Pewniejszą metodą liczenia jest:
Generowanie zmiennych losowych o rozkładzie Poissona
Prosty sposób na generowanie losowych liczb o rozkładzie Poissona, jest podany przez Knutha, zobacz odniesienia poniżej.
algorytm poisson random number (Knuth): init: Let L ← e^-λ, k ← 0 i p ← 1. do: k ← k + 1. Wygeneruj losową liczbę u z przedziału [0,1] i przypisz p ← p × u. while p > L. return k – 1.
Podczas gdy jest prosty, złożoność jest liniowa względem Istnieje wiele innych algorytmów na przezwyciężenie tego. Niektóre z nich są podane w Ahrens & Dieter, patrz odniesienia poniżej. Ponadto dla dużych wartości mogą być problemy ze stabilnością numeryczną ze względu na człon Jednym z rozwiązań dla dużych wartości jest Pobieranie z odrzuceniem, innym jest wykorzystanie przybliżenia Poissona przez Gaussa.
Metoda odwrotnej transformacji jest prosta i skuteczna dla małych wartości i wymaga tylko jednej jednolitej losowej liczby na próbkę. Skumulowane prawdopodobieństwa badane są z kolei, aż jedno przekracza
Estymacja parametrów
Największa wiarygodność
Dana jest próbka mierzonych wartości i chcemy oszacować wartość parametru populacji Poissona z której próbka została zaczerpnięta. Aby obliczyć wartość największej wiarygodności, tworzymy funkcję log-prawdopodobieństwo
Weź pochodną względem i przyrównaj ją do zera:
Rozwiązanie dla daje punkt stacjonarny, który, jeśli druga pochodna jest ujemna, jest oszacowaniem maksymalnego prawdopodobieństwa
Sprawdzając drugą pochodną, okazuje się, że jest ujemna dla wszystkich i większych od zera, dlatego ten stacjonarny punkt jest rzeczywiście maksimum początkowej funkcji prawdopodobieństwa:
Ponieważ każda obserwacja ma oczekiwane więc tak samo średnią tej próbki. Dlatego jest nieobciążonym estymatorem Jest to również efektywny estymator, tj. jego oszacowanie wariancji osiąga dolne ograniczenie nierówności Rao-Craméra. Stąd MVUE – estymator nieobciążony o minimalnej wariancji. Ponadto można udowodnić, że średnia próbki jest kompletna i wystarczająca statystycznie dla
Statystyka bayesowska
W statystyce bayesowskiej, sprzężony rozkład a priori dla parametru skali rozkładu Poissona jest rozkładem gamma. Niech
oznacza, że ma rozkład zgodnie z gęstością Gamma parametryzowaną ze względu na parametr kształtu i odwrotny parametrem skali:
Następnie biorąc tę samą próbkę zmierzonych wartości jak poprzednio, i a priori Gamma rozkład a posteriori jest
Średnia a posteriori zbliża się do oszacowania maksymalnego prawdopodobieństwa w granicy, jako
Przewidujący rozkład a posteriori dodatkowych danych jest rozkładem Gamma-Poissona (tj. ujemnym dwumianowym).
Przedział ufności
Prosta i szybka metoda obliczania przybliżonego przedziału ufności dla oszacowania jest zaproponowana w Guerriero et al. (2009). Metoda ta zapewnia dobre przybliżenie granic przedziału ufności dla próbek zawierających co najmniej 15–20 elementów. Oznaczając przez liczbę próbkowanych punktów lub zdarzeń, a przez długość linii próbek (lub przedział czasowy), górna i dolna granica 95% przedziału ufności dane są przez:
Prawo małych liczb
Słowo prawo jest czasami używane jako synonim rozkładu prawdopodobieństwa i konwergencja tu oznacza konwergencję w rozkładzie. W związku z tym rozkład Poissona jest czasami nazywany prawem małych liczb, ponieważ jest to rozkład prawdopodobieństwa ilości wystąpień zdarzenia, które zdarza się rzadko, ale ma bardzo wiele możliwości, aby się zdarzyć. Prawo małych liczb to książka Władysława Bortkiewicza o rozkładzie Poissona opublikowana w 1898 roku. Niektórzy historycy matematyki twierdzili, że rozkład Poissona powinien być nazywany rozkładem Bortkiewicza[6].
Zobacz też
- lemat Robbinsa
- losowanie Poissona
- niekompletna funkcja gamma
- proces Poissona
- regresja Poissona
- rozkład Conwaya-Maxwella-Poissona
- rozkład Erlanga
- rozkład Skellama
- rozkład Tweedie'go
- teoria kolejek
- teoria odnowy
- współczynnik zmienności
- wzór Dobińskiego
- złożony proces Poissona
Przypisy
- ↑ Jan Gullberg: Mathematics from the birth of numbers. New York: W.W. Norton, 1997, s. 963–965. ISBN 0-393-04002-X.
- ↑ NIST/SEMATECH, '6.3.3.1. Counts Control Charts', e-Handbook of Statistical Methods, accessed 25 October 2006.
- ↑ Peter McCullagh: Generalized Linear Models. Nelder, John. London: Chapman and Hall, 1989. ISBN 0-412-31760-5. page 196 gives the approximation and the subsequent terms.
- ↑ N.L. Johnson, S. Kotz, A.W. Kemp, Univariate Discrete distributions (2nd edition), Wiley, 1993, ISBN 0-471-54897-9, s. 163.
- ↑ Box, Hunter and Hunter: Statistics for experimenters. Wiley, s. 57.
- ↑ I.J. Good. Some statistical applications of Poisson’s work. „Statistical Science”. 1 (2), s. 157–180, 1986. DOI: 10.1214/ss/1177013690.
Bibliografia
- Rozkład po raz pierwszy tak nazwany w pracy:
- Herbert Edward Soper. Tables of Poisson’s exponential binomial limit. „Biometrika”. 10, s. 25–35, 1914.
Referencje
- J. Wawrzynek: Metody opisu i wnioskowania statystycznego. Wrocław: Wydawnictwo Akademii Ekonomicznej im. Oskara Langego we Wrocławiu, 2007, s. 56–57. ISBN 978-83-7011-859-4.
- V. Guerriero, S. Vitale, S. Ciarcia, S. Mazzoli. Improved statistical multi-scale analysis of fractures in carbonate reservoir analogues. „Tectonophysics”, 2011. Elsevier. DOI: 10.1016/j.tecto.2011.01.003.
- V. Guerriero, A. Iannace, S. Mazzoli, M. Parente, S. Vitale, M. Giorgioni. Quantifying uncertainties in multi-scale studies of fractured reservoir analogues: Implemented statistical analysis of scan line data from carbonate rocks. „Journal of Structural Geology”, 2009. Elsevier. DOI: 10.1016/j.jsg.2009.04.016.
- Donald E. Knuth: Seminumerical Algorithms. Addison Wesley, 1969, seria: The Art of Computer Programming, Volume 2.
- Joachim H. Ahrens, Ulrich Dieter. Computer Methods for Sampling from Gamma, Beta, Poisson and Binomial Distributions. „Computing”. 12 (3), s. 223–246, 1974. DOI: 10.1007/BF02293108.
- Joachim H. Ahrens, Ulrich Dieter. Computer Generation of Poisson Deviates. „ACM Transactions on Mathematical Software”. 8 (2), s. 163–179, 1982. DOI: 10.1145/355993.355997.
- Ronald J. Evans, J. Boersma, N.M. Blachman, A.A. Jagers. The Entropy of a Poisson Distribution: Problem 87-6. „SIAM Review”. 30 (2), s. 314–317, 1988. DOI: 10.1137/1030059.
Linki zewnętrzne
- POISSON () w najbardziej popularnych arkuszach kalkulacyjnych
- Kalkulator online – Rozkład Poissona
- p
- d
- e
| Rozkłady ciągłe | |
|---|---|
| Rozkłady dyskretne |
- Britannica: topic/Poisson-distribution
- БРЭ: 3172464
- SNL: poissonfordeling
- DSDE: Poisson-fordeling













![{\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\tfrac {\lambda ^{k}\ln(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fd292140a77c2d893e3db2d033e37721cb710a4)

















![{\displaystyle E[k],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f733636bd2ffa5c1d964780d7f67a433068037c)
![{\displaystyle \sigma _{k}^{2}=E[k^{2}]-E[k]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/451a3d0ceb8f6df590a02edb40e78482c4cfaf41)




























![{\displaystyle [0,t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d2d2fa44908c699e2b7b7b9e92befc8283f264)

















![{\displaystyle {\begin{aligned}\lim _{n\to \infty }P(X_{n}=k)&=\lim _{n\to \infty }{n \choose k}p^{k}(1-p)^{n-k}\\&=\lim _{n\to \infty }{\frac {n!}{(n-k)!k!}}\left({\frac {\lambda }{n}}\right)^{k}\left(1-{\frac {\lambda }{n}}\right)^{n-k}\\&=\lim _{n\to \infty }\underbrace {\left[{\frac {n!}{n^{k}(n-k)!}}\right]} _{A_{n}}\left({\frac {\lambda ^{k}}{k!}}\right)\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to \exp(-\lambda )}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\\&=\left[\lim _{n\to \infty }A_{n}\right]\left({\frac {\lambda ^{k}}{k!}}\right)\exp(-\lambda )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa7f42dc6ec21089663139448512fdd81b6eebb)

















































![{\displaystyle E[\lambda ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acd13b7450599d8fe8408749d3ba6c2b6ec4677c)















