Transfert radiatif

Cet article n’est pas rédigé dans un style encyclopédique (décembre 2022).

Vous pouvez améliorer sa rédaction !

Le transfert radiatif (ou transfert par rayonnement) est l'interaction du rayonnement électromagnétique avec la matière^[1], c'est-à-dire avec des particules matérielles de toutes natures (neutron, neutrino, ion, phonon...). Cette discipline permet notamment d'analyser la propagation des photons ou d'autres particules à travers un milieu gazeux, solide ou liquide. Cette propagation est affectée par les phénomènes d'émission, de réflexion, d'absorption et de diffusion qui sont traités par la physique atomique (propriétés spectroscopiques, diffusions Compton, Thomson, Mott, Møller), l'électromagnétisme (diffusion de Mie, réflexion et réfraction des interfaces) et la physique du solide (propriétés des surfaces : réflexion, émissivité).

Applications

Cette discipline permet notamment d'analyser la propagation des photons ou d'autres particules à travers un milieu gazeux, solide ou liquide. Historiquement, les premiers développements ont été réalisés dans le domaine de la physique des plasmas^{[2],[3][réf. incomplète]} et de l'astrophysique^[4]. Elle est aujourd'hui présente dans des domaines variés tels l'étude de l'atmosphère^[5], les problèmes de transfert thermique à haute température^{[6],[7],[8][réf. incomplète]} ou le rendu de génération d'image^{[9][réf. incomplète]}. Elle s'applique également à des particules autres que les photons, en neutronique^[10],[11], dans les problèmes d'irradiation, en particulier dans le domaine médical^[12], et en physique du solide pour le transport de phonons^[13].

Problèmes posés

Les problèmes posés sont de deux types :

• prévoir le rayonnement d'un système matériel ou les effets du rayonnement sur celui-ci. Les deux problèmes peuvent être disjoints ou couplés ;
• diagnostiquer les propriétés d'une source à partir de mesures externes^[7]. Cet aspect est particulièrement important en astrophysique, où les objets étudiés sont particulièrement lointains et où toute l'information est contenue dans les spectres mesurés. On le retrouve dans d'autres domaines où il est difficile de caractériser le milieu in situ : plasmas, haute atmosphère^[5], matériaux poreux, etc. Cet aspect relève du domaine des problèmes inverses et n'est pas traité ici.

Dans ce qui suit, on s'intéressera aux milieux gazeux, qui concentrent les problèmes rencontrés dans le domaine. On ignore ici les problèmes de toute autre nature posés par le rayonnement en milieu transparent tels qu'ils existent en thermique (méthode des facteurs de forme), ou en infographie tridimensionnelle.

Généralités

Le rayonnement en un point du milieu peut :

• subir une absorption, contribuant à chauffer le gaz ;
• être émis par une source imposée ou par les particules du gaz, ce phénomène étant très étroitement lié au précédent au niveau microscopique ;
• subir une diffusion, changeant sa direction et éventuellement sa fréquence.

Le rayonnement subit ainsi une variation quantitative et qualitative au cours de sa propagation, ce qui se traduit par une équation aux dérivées partielles contenant des dérivées par rapport au temps, aux variables de position et de direction de propagation : l'équation de transfert du rayonnement.

Le rayonnement dépend de :

• trois variables donnant la position dans l'espace ${\displaystyle \mathbf {r} }$ ;
• deux variables donnant la direction de propagation ${\displaystyle \mathbf {\Omega } }$. Dans ce qui suit on utilise les angles de colatitude (ou zénithal) ${\displaystyle \theta }$ et d'azimut (ou longitude) ${\displaystyle \phi }$ ;
• une variable de temps t ;
• une variable de longueur d'onde ${\displaystyle \lambda }$. On peut également utiliser la pulsation ${\displaystyle \lambda ^{-1}}$ (baptisée nombre d'onde en spectroscopie), la fréquence ${\displaystyle \nu =c/\lambda }$ ou l'énergie ${\displaystyle h\nu }$ ;

soit sept variables au total. Cette dimensionnalité rend difficile la résolution générale du transfert du rayonnement tant d'un point de vue théorique que numérique. De plus, le rayonnement a en général une influence sur la matière traversée, qui l'influence en retour. Il s'ensuit que le problème doit être résolu de manière couplée, itérative dans la plupart des cas.

Dans un grand nombre de situations l'échelle de temps radiative est très courte par rapport aux échelles de temps liées au fluide, de sorte que l'on peut supposer le transfert de rayonnement comme quasi-statique, éliminant ainsi la variable temporelle. Cette condition est réalisée dans un grand nombre de phénomènes mais pas toujours en physique des plasmas où l'on peut rencontrer des phénomènes violents.

Dans d'autres cas, le nombre de variables de position peut être réduit à deux ou à une seule si la géométrie du système s'y prête. Enfin, dans de rares cas, on peut ne considérer que les valeurs intégrées sur tout le spectre. Notons que certaines approximations décrites plus loin permettent de faire disparaître la dépendance angulaire explicite.

L'approche du phénomène est du type cinétique (analogue à la théorie cinétique des gaz) : les photons ont une trajectoire rectiligne entre deux interactions avec le milieu et la durée d'interaction est faible devant la durée qui sépare deux évènements. Ajoutons enfin que la présentation faite ici ignore la polarisation de la lumière^[3] ou une variation continue d'indice de réfraction du milieu^[3] qui fait apparaître des termes analogues à ceux présents dans l'équation eikonale. Ces problèmes se retrouvent entre autres dans les transferts atmosphériques ou les tomographies médicales. La vitesse de propagation est égale à la vitesse de la lumière ${\displaystyle c}$. Pour les milieux d'indice ${\displaystyle n}$ homogène différent de l'unité, on remplacera ${\displaystyle c}$ par la vitesse de groupe dans le milieu.

Intensité du rayonnement

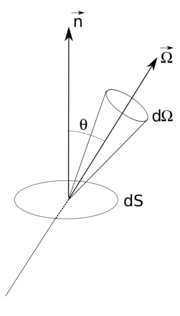
On caractérise le rayonnement par sa luminance^{[N 1]} spectrale ${\displaystyle L_{\nu }}$, une distribution angulaire définie de la façon suivante. En un point donné de l'espace, on considère un rayonnement contenu dans un angle solide ${\displaystyle \mathrm {d} {\mathit {\Omega }}=\sin \theta ~\mathrm {d} \theta ~\mathrm {d} \phi }$, dans un intervalle de fréquence ${\displaystyle [\nu ,\nu +\mathrm {d} \nu ]}$ et traversant une aire élémentaire ${\displaystyle \mathrm {d} \sigma =\mathrm {d} S\,\cos \theta }$ perpendiculaire à sa direction de propagation. La quantité d'énergie ${\displaystyle \mathrm {d} {\mathcal {E}}_{\nu }}$ des photons est proportionnelle à ${\displaystyle \mathrm {d} \sigma \mathrm {d} \nu \mathrm {d} {\mathit {\Omega }}\mathrm {d} t}$, ce que l'on peut écrire :

${\displaystyle \mathrm {d} {\mathcal {E}}_{\nu }\,=\,L_{\nu }\,\mathrm {d} \sigma \,\mathrm {d} \nu \,\mathrm {d} {\mathit {\Omega }}\,\mathrm {d} t}$

La luminance spectrale ${\displaystyle L_{\nu }}$ est donc l'énergie par unités d'aire, de temps, de fréquence et d'angle solide traversant une surface perpendiculaire au faisceau de rayonnement. Il s'agit donc d'une quantité positive ou nulle. La quantité ${\displaystyle L_{\nu }\mathrm {d} \nu }$, représentant le flux angulaire d'énergie, s'exprime en W m⁻² sr⁻¹ dans le système international d'unités ou en erg s⁻¹ cm⁻² sr⁻¹ dans le système CGS (obsolète, mais encore utilisé dans certains domaines).

Si on se réfère à la longueur d'onde et non pas à la fréquence, la quantité ${\displaystyle L_{\lambda }\mathrm {d} \lambda }$ représentant également le flux angulaire, ${\displaystyle L_{\lambda }}$ n'est pas égale à ${\displaystyle L_{\nu }}$ et n'a pas les mêmes dimensions physiques. L'équivalence des deux écritures permet d'écrire

${\displaystyle L_{\lambda }\delta \lambda \,=\,L_{\nu }\delta \nu }$

et, puisque ${\displaystyle \lambda =c/\nu }$,

${\displaystyle L_{\lambda }=L_{\nu }\,\delta \nu /\delta \lambda =L_{\nu }\,|\mathrm {d} \nu /\mathrm {d} \lambda |=(\nu ^{2}/c)L_{\nu }=(c/\lambda ^{2})L_{\nu }}$

La présence d'une valeur absolue dans cette expression est liée au fait que ${\displaystyle \delta \lambda }$ et ${\displaystyle \delta \nu }$ sont comptés positivement. Il résulte de ces expressions que ${\displaystyle L_{\nu }}$ se mesure en J m⁻² sr⁻¹ et ${\displaystyle L_{\lambda }}$ en W m⁻³ sr⁻¹.

Comme indiqué plus haut, l'intensité du rayonnement est fonction du point considéré, de la direction, de la fréquence et du temps : ${\displaystyle L_{\nu }=L_{\nu }(\mathbf {r} ,t,\mathbf {\Omega } ,\nu )}$

En physique statistique, la luminance est liée à la densité numérique de photons dans le milieu ${\displaystyle f_{\nu }}$ par

${\displaystyle L_{\nu }=ch\nu f_{\nu }}$

Moments de la luminance

Les moments de la luminance sont définis par l'intégration angulaire de ${\displaystyle L_{\nu }}$ après multiplication par ${\displaystyle 1,\mathbf {\Omega } ,\mathbf {\Omega } \otimes \mathbf {\Omega } ,...}$, où ${\displaystyle \otimes }$ est le produit tensoriel. Ces quantités jouent un rôle important. Elles sont définies dans ce qui suit.

D'autres propriétés sont également déduites de la luminance : elles concernent le rayonnement en milieu transparent.

Énergie radiative

L'énergie volumique spectrale est l'intégrale de l'intensité dans tout l'espace angulaire divisée par ${\displaystyle c}$ (unité J.s.m^-3)

${\displaystyle E_{\nu }(\mathbf {r} ,t,\nu )={\frac {1}{c}}\int _{4\pi }\,L_{\nu }(\theta ,\phi )\,\mathrm {d} {\mathit {\Omega }}\equiv {\frac {1}{c}}\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{\pi }L_{\nu }(\theta ,\phi )\,\sin \theta \,\mathrm {d} \theta }$

Si la luminance est de révolution (indépendante de l'azimut ${\displaystyle \phi }$), on a

${\displaystyle E_{\nu }={\frac {2\pi }{c}}\int _{0}^{\pi }L_{\nu }(\theta )\,\sin \theta \,\mathrm {d} \theta ={\frac {2\pi }{c}}\int _{-1}^{1}L_{\nu }(\mu )\mathrm {d} \mu }$

où ${\displaystyle \mu =\cos ~\theta }$. Ce changement de variable permet simplement de condenser l'écriture. L'indépendance azimutale permet de réduire l'espace des variables d'une unité.

Si le milieu est à l'équilibre thermodynamique le rayonnement est celui d'un corps noir : il est isotrope et l'intensité lumineuse suit la loi de Planck

${\displaystyle L_{\nu }\,=L_{\nu }^{\circ }={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{h\nu /kT}-1}}}$

L'énergie vaut dans ce cas ${\displaystyle E_{\nu }={\frac {4\pi L_{\nu }^{\circ }}{c}}}$.

L'intégration sur tout le spectre donne l'énergie volumique totale (unité SI : J/m³) :

${\displaystyle E(\mathbf {r} ,t)=\int _{0}^{\infty }E_{\nu }\mathrm {d} \nu =aT^{4}}$

avec^[14] ${\displaystyle a={\frac {8\pi ^{5}k^{4}}{15h^{3}c^{3}}}=7.565865\times 10^{-16}~\mathrm {J\cdot m^{-3}\cdot K^{-4}} }$

Pour effectuer cette intégration, on a utilisé le changement de variable ${\displaystyle x={\frac {h\nu }{kT}}}$ et la relation ${\displaystyle \int _{0}^{\infty }{\frac {x^{3}}{\mathrm {e} ^{x}-1}}\mathrm {d} x={\frac {\pi ^{4}}{15}}}$

Dans le cas général, on utilise parfois une température apparente, ou effective, notée T_eff et définie par ${\displaystyle E=aT_{\mathrm {eff} }^{4}}$. La quantité ${\displaystyle T_{\mathrm {eff} }}$ est la température du corps noir correspondant à l'énergie ${\displaystyle E}$ et n'a pas de signification physique particulière.

Flux radiatif et exitance

Le vecteur correspondant à la densité de flux spectral à travers la surface ${\displaystyle dS}$ est le moment d'ordre 1 de l'intensité (unitéJ m⁻²)

${\displaystyle \mathbf {M} _{\nu }(\mathbf {r} ,t,\nu )=\int _{4\pi }L_{\nu }\mathbf {\Omega } \mathrm {d} {\mathit {\Omega }}}$

Le module de sa projection sur la normale à une surface est appelé exitance.

On utilise également le flux adimensionné

${\displaystyle \mathbf {f} _{\nu }(\mathbf {r} ,t,\nu )={\frac {\mathbf {M} _{\nu }}{cE_{\nu }}}}$

Sa norme mesure l'anisotropie. Un rayonnement isotrope a un flux nul donc ${\displaystyle f_{\nu }=||\mathbf {f} _{\nu }||=0}$. Le flux maximal est obtenu lorsque toute l'énergie est transportée avec la vitesse c : sa valeur est alors ${\displaystyle cE_{\nu }}$ donc dans ce cas ${\displaystyle f_{\nu }=\pm 1}$. Cette dernière situation décrit un faisceau parallèle comme un faisceau laser.

Dans le cas unidimensionnel plan défini par un axe quelconque, le module du flux mesuré sur l'axe s'écrit

${\displaystyle M_{\nu }=\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{\pi }L_{\nu }(\theta ,\phi )\cos \theta \sin \theta \mathrm {d} \theta }$

Si de plus la luminance est de révolution, cette expression devient

${\displaystyle M_{\nu }\,=\,2\pi \int _{0}^{\pi }L_{\nu }(\theta )\,\cos \theta \,\sin \theta \,\mathrm {d} \theta \,=\,2\pi \int _{-1}^{1}L_{\nu }(\mu )\mu \mathrm {d} \mu }$

On peut scinder cette expression en découpant l'espace en deux parties, l'une pour les rayons allant dans le sens - vers + et l'autre pour le sens opposé. On note ${\displaystyle L_{\nu }^{+}}$ et ${\displaystyle L_{\nu }^{-}}$ les intensités dans chaque demi-espace. Les flux correspondants sont notés ${\displaystyle M_{\nu }^{+}}$ et ${\displaystyle M_{\nu }^{-}}$, de telle sorte que ${\displaystyle M_{\nu }\,=M_{\nu }^{+}-M_{\nu }^{-}}$. Ces valeurs sont données par

${\displaystyle M_{\nu }^{+}=2\pi \int _{0}^{1}L_{\nu }^{+}\mu \mathrm {d} \mu }$

${\displaystyle M_{\nu }^{-}=2\pi \int _{-1}^{0}L_{\nu }^{-}\mu \mathrm {d} \mu }$

Pour une luminance isotrope, on a ${\displaystyle M_{\nu }^{+}=\pi L_{\nu }^{+}}$ : c'est la loi de Lambert.

Si de plus on est à l'équilibre thermodynamique, on obtient par intégration sur les fréquences la loi de Stefan : ${\displaystyle M^{+}(\mathbf {r} ,t)=M^{-}={\frac {cE}{4}}=\sigma T^{4}}$ où ${\displaystyle \sigma ={\frac {ac}{4}}}$ est la constante de Stefan-Boltzmann.

Ces expressions sont d'un intérêt faible ici, mais elles prennent tout leur sens lorsque l'espace est scindé en deux parties par une barrière physique opaque. Elles décrivent alors les propriétés radiatives de la surface de telles barrières.

Une hypothèse simplificatrice consistera à supposer a priori que la luminance est isotrope dans chaque demi-espace. Cette méthode est due à Arthur Schuster (1905)^[15] et Karl Schwarzschild (1906)^[16]. Ce faisant, on élimine la dépendance angulaire du problème au prix d'une multiplication par deux du nombre d'équations. Cette méthode se généralise au problème bidimensionnel en utilisant un découpage de l'espace en 4 quadrants et au problème tridimensionnel par un découpage en 8 octants, ce qui multiplie respectivement par 4 et 8 le nombre d'équations. Malgré cela, le gain en temps de calcul reste important. On note que, dans ce cas, la distribution angulaire est discontinue, ce qui n'est pas gênant en soi. Toutefois, la discontinuité mesure la précision de la méthode, généralement médiocre.

Pression radiative

La pression est le tenseur d'ordre 2 symétrique (unité J.s.m^-3)

${\displaystyle {\mathsf {P}}_{\nu }(\mathbf {r} ,t,\nu )={\frac {1}{c}}\int _{4\pi }L_{\nu }\,\mathbf {\Omega } \otimes \mathbf {\Omega } \mathrm {d} \Omega }$

Si l'intensité est isotrope le tenseur de pression s'exprime en fonction du tenseur unité ${\displaystyle {\mathsf {I}}=[\delta _{ij}]}$, ${\displaystyle \delta _{ij}}$ étant le symbole de Kronecker

${\displaystyle {\mathsf {P}}_{\nu }={\frac {L_{\nu }(\mathbf {r} ,t,\nu )}{c}}\int _{4\pi }\mathbf {\Omega } \otimes \mathbf {\Omega } \mathrm {d} \Omega ={\frac {1}{3c}}L_{\nu }{\mathsf {I}}}$

La pression est donc également isotrope. On verra que la proposition inverse n'est pas vraie.

Dans le cas du corps noir on peut intégrer en fréquence comme cela a été fait ci-dessus pour l'énergie et la pression vaut alors (unité J.m^-3)

${\displaystyle {\mathsf {P}}={\frac {1}{3}}aT^{4}{\mathsf {I}}}$

Il n'est pas nécessaire d'avoir des températures extrêmement élevées pour que la pression radiative concurrence la pression du fluide. Un exemple en est le radiomètre de Nichols^[17]. Cette notion de pression est utilisée pour calculer l'effort s'exerçant sur une surface comme dans le cas d'une voile solaire.

Plutôt que la pression on utilise le tenseur d'Eddington sans dimension ${\displaystyle {\mathsf {D}}_{\nu }={\frac {{\mathsf {P}}_{\nu }}{E_{\nu }}}}$. La valeur propre non nulle de la matrice correspondante est le coefficient d'Eddington ${\displaystyle \chi _{\nu }}$. Le vecteur propre correspondant est le vecteur unitaire de propagation du flux ${\displaystyle \mathbf {k} _{\nu }={\frac {\mathbf {f} _{\nu }}{f_{\nu }}}}$.

Si le problème est à symétrie azimutale on peut montrer que le tenseur d'Eddington peut s'écrire sous la forme

${\displaystyle {\mathsf {D}}_{\nu }={\frac {1-\chi _{\nu }}{2}}\mathrm {I} +{\frac {3\chi _{\nu }-1}{2}}\mathbf {k} _{\nu }\otimes \mathbf {k} _{\nu }}$

Il est la somme d'un terme isotrope et d'un faisceau parallèle. ${\displaystyle \chi _{\nu }={\frac {1}{3}}}$ correspond au cas isotrope et ${\displaystyle \chi _{\nu }=1}$ au faisceau.

Équation de transfert

Quand le rayonnement traverse un milieu contenant des particules (atomes neutres ou ionisés, électrons, molécules neutres ou ionisées, grains de matière, etc.), cette matière est susceptible d'absorber, d'émettre ou de diffuser de l'énergie lumineuse.

Absorption

On caractérise la capacité d'absorption du milieu contenant n particules actives par unité de volume par la section efficace ${\displaystyle \Sigma _{\nu }}$ ou le coefficient d'absorption ${\displaystyle \kappa _{\nu }=n\Sigma _{\nu }}$, qui a la dimension de l'inverse d'une longueur et est défini de telle sorte que la quantité sans dimension ${\displaystyle \kappa _{\nu }ds}$ représente la fraction de rayonnement absorbée le long du trajet ${\displaystyle \mathrm {d} s}$. Cette quantité définit l'épaisseur optique de la couche infinitésimale

${\displaystyle \mathrm {d} \tau _{\nu }\,=\,\kappa _{\nu }\,\mathrm {d} s}$ soit ${\displaystyle \tau _{\nu }\,=\,\int _{0}^{s}\kappa _{\nu }\,\mathrm {d} s}$

Pour un milieu à une dimension d'espace l'absorption seule conduit à une décroissance exponentielle de la luminance ${\displaystyle L_{\nu }(\tau _{\nu })=L_{\nu }(0)e^{-\tau _{\nu }}}$ (loi de Beer-Lambert). ${\displaystyle e^{-\tau _{\nu }}}$ est la probabilité pour que le photon ne soit pas absorbé. Le libre parcours moyen ${\displaystyle l}$ est défini par ${\displaystyle {\overline {\tau _{\nu }}}=\kappa _{\nu }l}$. Or ${\displaystyle {\overline {\tau _{\nu }}}=\int _{0}^{\infty }\tau _{\nu }e^{-\tau _{\nu }}\mathrm {d} \tau _{\nu }=1}$, donc ${\displaystyle l=\kappa _{\nu }^{-1}}$.

Si on prend la longueur d'onde au lieu de la fréquence comme variable, le coefficient d'absorption ${\displaystyle \kappa _{\lambda }}$ est tel que ${\displaystyle \kappa _{\lambda }=\kappa _{\nu }}$

Émission, fonction source

Le milieu peut contenir une source notée ${\displaystyle S_{\nu }}$. Celle-ci peut être ponctuelle, linéique, surfacique ou volumique. Un cas important d'émission en volume est celui du gaz. On définit un coefficient d'émission spontanée ${\displaystyle \epsilon _{\nu }}$ relié à l'absorption par les mécanismes microscopiques (coefficients d'Einstein). À l'équilibre thermodynamique local ${\displaystyle \epsilon _{\nu }=\kappa _{\nu }L_{\nu }^{\circ }}$ où ${\displaystyle L_{\nu }^{\circ }}$ est la distribution de Planck définie plus haut.

Diffusion

L'interaction d'un photon avec une particule chargée ou un objet solide de taille voisine de la longueur d'onde donne lieu à un phénomène de déviation et éventuellement un changement de fréquence. La diffusion^{[N 2]} (en anglais scattering) est caractérisée par sa probabilité de réalisation pour l'intervalle de fréquence ${\displaystyle [\nu ,\nu +\mathrm {d} \nu ]}$, sur le trajet ${\displaystyle \mathrm {d} s}$, valant ${\displaystyle \Theta _{\nu }\mathrm {d} s}$, et comportant deux parties, l'une pour la transition directe (création) ${\displaystyle \Theta _{\nu }^{+}}$ et l'autre pour le phénomène inverse (disparition) ${\displaystyle \Theta _{\nu }^{-}}$

${\displaystyle {\begin{array}{lcl}\Theta _{\nu }^{+}&=&\int _{0}^{\infty }n\sigma _{\nu }(\nu '\rightarrow \nu ){\mathcal {P}}_{\nu }(\mathbf {\Omega } '\rightarrow \mathbf {\Omega } )\mathrm {d} \nu '\\[0.5em]\Theta _{\nu }^{-}&=&\int _{0}^{\infty }n\sigma _{\nu }(\nu \rightarrow \nu '){\mathcal {P}}_{\nu }(\mathbf {\Omega } \rightarrow \mathbf {\Omega } ')\mathrm {d} \nu '\end{array}}}$

Le phénomène est proportionnel au nombre de diffuseurs par unité de volume ${\displaystyle n}$ et pour chaque intervalle ${\displaystyle [\nu ',\nu '+\mathrm {d} \nu ']}$ à leur section efficace spectrale ${\displaystyle \sigma _{\nu }(\nu \rightarrow \nu ')}$ (unité m² s).

La déviation est caractérisée par la fonction de répartition ${\displaystyle {\mathcal {P}}_{\nu }(\mathbf {\Omega } \rightarrow \mathbf {\Omega } ')}$ (en anglais phase function) normalisée par ${\displaystyle \int _{4\pi }{\mathcal {P}}_{\nu }\mathrm {d} \Omega =1}$. Cette distribution est généralement axisymétrique par rapport au rayon incident et ne dépend que de l'angle ${\displaystyle (\mathbf {\Omega } ,\mathbf {\Omega } ')}$ que l'on peut caractériser par son cosinus dont la valeur est donnée par le produit scalaire ${\displaystyle \mathbf {\Omega } \cdot \mathbf {\Omega } '}$.

Le terme de diffusion s'écrira donc en intégrant sur tous les ${\displaystyle \mathbf {\Omega } '}$

${\displaystyle \epsilon _{\nu }^{d}=\int _{4\pi }\left[\Theta _{\nu }^{+}L_{\nu }(\nu ',\mathbf {\Omega } ')-\Theta _{\nu }^{-}L_{\nu }(\nu ,\mathbf {\Omega } )\right]\mathrm {d} \Omega '}$

On peut simplifier cette expression en sortant ${\displaystyle L_{\nu }(\nu ,\mathbf {\Omega } )}$ de l'intégrale et en tenant compte de la normalisation de ${\displaystyle {\mathcal {P}}_{\nu }}$

${\displaystyle \epsilon _{\nu }^{d}=\int _{0}^{\infty }n\sigma _{\nu }'\int _{4\pi }{\mathcal {P}}_{\nu }(\mathbf {\Omega } \cdot \mathbf {\Omega } ')L_{\nu }(\nu ',\mathbf {\Omega } ')d\Omega '\mathrm {d} \nu '-L_{\nu }(\nu ,\mathbf {\Omega } )\int _{0}^{\infty }n\sigma _{\nu }'\mathrm {d} \nu '}$

Cette expression fait apparaître le coefficient ${\displaystyle \kappa _{\nu }^{d}=\int _{0}^{\infty }n\sigma _{\nu }'\mathrm {d} \nu '}$ qui caractérise l'extinction de l'intensité ${\displaystyle L_{\nu }}$. On remarque que l'effet produit sur l'intensité est identique à celui caractérisant l'absorption. On pourra donc définir un coefficient d'extinction totale ${\displaystyle \kappa _{\nu }^{t}=\kappa _{\nu }+\kappa _{\nu }^{d}}$. Dans ce terme la part de la diffusion est l'albédo ${\displaystyle \omega _{\nu }={\frac {\kappa _{\nu }^{d}}{\kappa _{\nu }^{t}}}}$

Cette équation, valide pour la diffusion Compton se simplifie pour une diffusion élastique (sans changement de fréquence) comme les diffusions Thomson, de Mie ou Rayleigh. Dans ce cas on définit une section efficace ${\displaystyle \Sigma _{\nu }}$ telle que

${\displaystyle {\begin{array}{lcl}\Theta _{\nu }^{+}&=&n\Sigma _{\nu }{\mathcal {P}}_{\nu }(\mathbf {\Omega } '\rightarrow \mathbf {\Omega } )\\[0.5em]\Theta _{\nu }^{-}&=&n\Sigma _{\nu }{\mathcal {P}}_{\nu }(\mathbf {\Omega } \rightarrow \mathbf {\Omega } ')\end{array}}}$

Le terme de diffusion devient

${\displaystyle \epsilon _{\nu }^{d}=\kappa _{\nu }^{d}\int _{4\pi }{\mathcal {P}}_{\nu }(\mathbf {\Omega } \cdot \mathbf {\Omega } ')L_{\nu }(\nu ',\mathbf {\Omega } ')\mathrm {d} \Omega '-\kappa _{\nu }^{d}L_{\nu }(\nu ,\mathbf {\Omega } )}$

avec ${\displaystyle \kappa _{\nu }^{d}=n\Sigma _{\nu }}$

Équation de transfert du rayonnement

En plus des méthodes de conservation décrites ci-dessous, l'équation de transfert peut être déduite de l'équation de Maxwell par passage à la limite ${\displaystyle \nu \to \infty }$^[18].

Formulation sous forme intégro-différentielle

L'équation de transfert du rayonnement établit le bilan d'énergie pour l'intervalle de fréquence ${\displaystyle \mathrm {d} \nu }$ dans un volume ${\displaystyle \mathrm {d} s\mathrm {d} \sigma =c\mathrm {d} t\mathrm {d} \sigma }$, dans l'angle solide ${\displaystyle \mathrm {d} \Omega }$

${\displaystyle \left[L_{\nu }(\mathbf {r} +\mathbf {\Omega } \mathrm {d} s,t+\mathrm {d} t,\mathbf {\Omega } )-L_{\nu }(\mathbf {r} ,t,\mathbf {\Omega } )\right]\mathrm {d} \sigma \mathrm {d} \Omega \mathrm {d} t\mathrm {d} \nu =\left[\epsilon _{\nu }-\kappa _{\nu }^{t}L_{\nu }(\mathbf {r} ,t,\mathbf {\Omega } )+\int _{0}^{\infty }n\sigma _{\nu }'\int _{4\pi }{\mathcal {P}}_{\nu }(\mathbf {\Omega } \cdot \mathbf {\Omega } ')L_{\nu }(\nu ',\mathbf {\Omega } ')\mathrm {d} \Omega '\mathrm {d} \nu '\right]\mathrm {d} s\mathrm {d} \sigma \mathrm {d} \Omega \mathrm {d} t\mathrm {d} \nu }$

• Le terme de gauche est la variation spatio-temporelle dans le volume de référence ;
• les termes de droite représentent les sources et puits d'énergie.

or un développement de Taylor permet d'écrire

${\displaystyle L_{\nu }(\mathbf {r} +\mathbf {\Omega } \mathrm {d} s,t+\mathrm {d} t,\mathbf {\Omega } )-L_{\nu }(\mathbf {r} ,t,\mathbf {\Omega } )=\left({\frac {1}{c}}{\frac {\partial L_{\nu }}{\partial t}}+{\frac {\partial L_{\nu }}{\partial s}}\right)\mathrm {d} s=\left({\frac {1}{c}}{\frac {\partial L_{\nu }}{\partial t}}+\mathbf {\Omega } \cdot \nabla L_{\nu }\right)\mathrm {d} s}$

de sorte que l'on obtient l'équation de transfert du rayonnement sous la forme (dans le cas de la diffusion élastique)

${\displaystyle {\frac {1}{c}}{\frac {\partial L_{\nu }}{\partial t}}+\mathbf {\Omega } \cdot \nabla L_{\nu }+\kappa _{\nu }^{t}L_{\nu }=\epsilon _{\nu }+2\pi \kappa _{\nu }^{d}\int _{-1}^{1}{\mathcal {P}}_{\nu }L_{\nu }\mathrm {d} \mu }$

Cette équation est également connue sous le nom d'équation de Boltzmann à cause de son analogie avec l'équation décrivant les milieux gazeux. Le terme de droite représente la production totale.

Dans un milieu d'indice différent de l'unité

Dans un milieu d'indice ${\displaystyle n_{\nu }}$, la luminance est liée à la densité numérique de photons ${\displaystyle f_{\nu }}$ par :

${\displaystyle L_{\nu }=v_{g_{\nu }}h\nu f_{\nu }}$

où ${\displaystyle v_{g_{\nu }}=c\left[{\frac {\mathrm {d} }{\mathrm {d} \nu }}(\nu n_{\nu })\right]^{-1}}$ est la vitesse de groupe dans le milieu ; pour un milieu non dispersif, elle est égale à la vitesse de phase ${\displaystyle {\frac {c}{n_{\nu }}}}$.

Par rapport au milieu d'indice unité, ${\displaystyle f_{\nu }}$ est multiplié par ${\displaystyle n_{\nu }^{2}}$^[18].

La nouvelle équation de transfert s'écrit^[3] :

${\displaystyle {\frac {1}{v_{g_{\nu }}}}{\frac {\partial }{\partial t}}\left({\frac {L_{\nu }}{n_{\nu }^{2}}}\right)+\mathbf {\Omega } \cdot \nabla \left({\frac {L_{\nu }}{n_{\nu }^{2}}}\right)+{\frac {\nabla n_{\nu }}{n_{\nu }}}\cdot \nabla _{S^{2}}\left({\frac {L_{\nu }}{n_{\nu }^{2}}}\right)+\kappa _{\nu }^{t}\left({\frac {L_{\nu }}{n_{\nu }^{2}}}\right)={\frac {\epsilon _{\nu }}{n_{\nu }^{2}}}+2\pi \kappa _{\nu }^{d}\int _{-1}^{1}{\mathcal {P}}_{\nu }{\frac {L_{\nu }}{n_{\nu }^{2}}}\mathrm {d} \mu }$

où ${\displaystyle \nabla _{S^{2}}}$ est le gradient sur la sphère unité^{[N 3]}.

Par rapport à l'équation dans le vide, le nouveau terme qui apparaît contient ${\displaystyle {\frac {\nabla n_{\nu }}{n_{\nu }}}}$, qui est égal à la réfraction ${\displaystyle {\frac {\mathrm {d} \Omega }{\mathrm {d} s}}}$ du rayon d'orientation ${\displaystyle \Omega }$ le long de sa trajectoire mesurée par l'abscisse curviligne ${\displaystyle s}$.

Formulation sous forme intégrale

On peut décrire la luminance au point ${\displaystyle \mathbf {r} }$, dans la direction ${\displaystyle \mathbf {\Omega } }$ comme la somme de tous les rayons arrivant en ce point et provenant de ${\displaystyle \mathbf {r} -s\mathbf {\Omega } }$ avec ${\displaystyle s=|\mathbf {r} -\mathbf {r'} |}$, produits à l'instant ${\displaystyle t-{\frac {s}{c}}}$. En cette origine on a un terme source ${\displaystyle S_{\nu }}$ qui correspond soit à une émission, soit résulte d'une diffusion ${\displaystyle (\nu '\rightarrow \nu ,\mathbf {\Omega } '\rightarrow \mathbf {\Omega } )}$. Dans ce dernier cas il s'écrit

${\displaystyle S_{\nu }=\int _{4\pi }\Theta _{\nu }^{+}L_{\nu }\left(\nu ',\mathbf {\Omega } ',\mathbf {r} -s\mathbf {\Omega } ,t-{\frac {s}{c}}\right)\mathrm {d} \Omega '}$

La luminance au point ${\displaystyle \mathbf {r} }$ est obtenue par intégration sur la ligne de visée ${\displaystyle (-\mathbf {\Omega } )}$

${\displaystyle L_{\nu }(\mathbf {r} ,t,\nu )=\int _{0}^{\infty }S_{\nu }\left(\mathbf {r} -s\mathbf {\Omega } ,t-{\frac {s}{c}}\right)e^{-\int _{0}^{s}\kappa _{\nu }\left(\mathbf {r} -s'\mathbf {\Omega } ,t-{\frac {s'}{c}}\right)\mathrm {d} s'}\mathrm {d} s}$

Cette expression explicite n'est utilisable que dans un nombre limité de situations.

Solutions analytiques

Solutions directes

Les solutions analytiques sont rares. On peut citer le cas du milieu infini, homogène, à diffusion isotrope, pour lequel on peut écrire l'équation du transfert radiatif de ${\displaystyle L_{\nu }(\tau _{\nu },\mu )}$ sous la forme suivante :

${\displaystyle \mu {\frac {\partial L_{\nu }}{\partial \tau _{\nu }}}+L_{\nu }=S_{\nu }(\mu )+{\frac {\omega _{\nu }}{2}}\int _{-1}^{1}L_{\nu }\mathrm {d} \mu }$

• Premier cas : absorption seulement ${\displaystyle \omega _{\nu }=0,\;S_{\nu }=0,\;\tau _{\nu }=\kappa _{\nu }x}$.

Si la condition à la limite sur le plan défini par ${\displaystyle x=0}$ est un rayon dans la direction ${\displaystyle \mu =1}$ (perpendiculaire à la surface) la solution est

${\displaystyle L_{\nu }(\tau _{\nu },\mu =1)=L_{\nu }(0)e^{-\tau _{\nu }}}$

Il s'agit de la loi de Beer-Lambert.

Pour une source isotrope ${\displaystyle L_{0}}$ la solution s'écrit

${\displaystyle L_{\nu }(\tau _{\nu },\mu )=L_{0}e^{-{\frac {\tau _{\nu }}{\mu }}}}$

La distribution angulaire (voir ci-contre), quasi-isotrope près de l'origine, devient de plus en plus orientée : les rayons proches de la perpendiculaire à la surface parcourent un chemin optique plus faible et deviennent dominants.

• Absorption et émission.

La solution est simplement la solution précédente à laquelle on ajoute la fonction source qui devient prépondérante quand on s'éloigne de l'origine.

• Absorption et diffusion ${\displaystyle \tau _{\nu }=(\kappa _{\nu }+\kappa _{\nu }^{d})\,x}$.

La solution de cette équation intégro-différentielle peut être obtenue par la méthode de Wiener-Hopf ou par l'étude des valeurs propres singulières de l'opérateur de transport associé à l'équation de Boltzmann^[19]. Après de longs calculs on obtient pour la propagation de gauche à droite

${\displaystyle L_{\nu }(\tau _{\nu }>0,\mu )=L_{0}\left[{\frac {\omega _{\nu }\beta _{\nu }}{\beta _{\nu }-\mu }}e^{-{\frac {\tau _{\nu }}{\beta _{\nu }}}}+\int _{0}^{1}B(\gamma ,\mu )e^{-{\frac {\tau _{\nu }}{\gamma }}}\mathrm {d} \gamma \right]}$

où ${\displaystyle \beta _{\nu }}$ est solution de l'équation transcendante

${\displaystyle {\rm {artanh}}\,\beta _{\nu }\,=\omega _{\nu }^{-1}\beta _{\nu }^{-1}\;\rightarrow \;0<\beta _{\nu }^{-1}<1}$

Le premier terme correspond à la décroissance la plus lente et constitue donc la solution pour les x grands. ${\displaystyle \beta _{\nu }\,\,>\,1}$ : la décroissance est plus lente que ${\displaystyle e^{-\tau _{\nu }}}$. La distribution angulaire (voir figure ci-contre) comporte, par rapport à la précédente, un terme isotrope qui devient prépondérant lorsqu'on s'éloigne de l'origine. Au total la solution loin de l'origine est une distribution isotrope décroissant lentement.

La propagation de droite à gauche est isotrope. En particulier, on est capable de donner le rayonnement sortant du milieu vers la gauche. Ce type de calcul est utilisable pour connaître l'émissivité de la surface d'un milieu semi-transparent ou sa réflectivité bidirectionnelle.

• Diffusion seule.

Dans le cas d'une source isotrope la solution triviale du problème est ${\displaystyle L_{\nu }=L_{0}}$. La source est propagée sans modification dans tout le milieu.

Méthodes intégrales

Il est possible dans quelques cas d'obtenir la solution générale en calculant la distribution de Green K du problème. La solution s'exprime alors comme le produit de convolution

${\displaystyle E_{\nu }(\tau _{\nu })=\int _{-\infty }^{\infty }K(\tau _{\nu }-\tau _{\nu }')S_{\nu }(\tau _{\nu }')\mathrm {d} \tau _{\nu }'}$

Cette équation est nommée équation de Schwarzschild-Milne (1921). La méthode est théoriquement applicable quel que soit le terme source ${\displaystyle S_{\nu }}$. En pratique les solutions analytiques du problème avec diffusion sont rares et limitées à des cas simples comme un milieu homogène (propriétés constantes), une diffusion isotrope, en géométrie à une dimension plane, cylindrique ou sphérique. La résolution fait appel à des méthodes mathématiques telles que les transformations de Laplace ou de Fourier. Ces solutions sont utilisées comme référence pour tester des approximations (tests de performance).

Prenons l'exemple d'un milieu à une dimension d'espace en stationnaire, sans diffusion. La luminance s'écrit en projetant l'expression ci-dessus sur un axe x quelconque et en utilisant la profondeur optique ${\displaystyle \tau _{\nu }}$ définie plus haut

• pour la partie - vers +

${\displaystyle L_{\nu }^{+}(\tau _{\nu },\mu >0)=\int _{-\infty }^{\tau _{\nu }}S_{\nu }(\tau ')e^{-{\frac {\tau _{\nu }-\tau _{\nu }'}{\mu }}}{\frac {d\tau _{\nu }'}{\mu }}}$

• pour la partie + vers -

${\displaystyle L_{\nu }^{-}(\tau _{\nu },\mu <0)=\int _{\tau _{\nu }}^{\infty }S_{\nu }(\tau _{\nu }')e^{-{\frac {\tau _{\nu }'-\tau _{\nu }}{\mu }}}{\frac {d\tau _{\nu }'}{\mu }}}$

L'énergie vaut donc

${\displaystyle E_{\nu }={\frac {2\pi }{c}}\int _{0}^{1}L_{\nu }^{+}d\mu +{\frac {2\pi }{c}}\int _{-1}^{0}L_{\nu }^{-}d\mu }$

En faisant le changement de variable ${\displaystyle y={\frac {1}{\mu }}}$ dans le premier terme, ${\displaystyle y=-{\frac {1}{\mu }}}$ dans le second et en intervertissant les intégrales il vient

${\displaystyle E_{\nu }={\frac {2\pi }{c}}\int _{-\infty }^{\infty }S_{\nu }(\tau _{\nu }')\int _{1}^{\infty }e^{-y(\tau _{\nu }-\tau _{\nu }')}{\frac {dy}{y}}d\tau _{\nu }'={\frac {2\pi }{c}}\int _{-\infty }^{\infty }S_{\nu }(\tau _{\nu }')E_{1}(\tau _{\nu }-\tau _{\nu }')d\tau _{\nu }'}$

où ${\displaystyle E_{1}}$ est l'exponentielle intégrale qui constitue la fonction (ou noyau) de Green du problème.

 

Approximations

On décrit ci-dessous brièvement les méthodes les plus courantes de résolution ou d'approximation.

Méthodes directes

Dans le cas de milieux transparents l'approche du calcul de la luminance en un point à partir des sources est possible. De cette façon on peut calculer les facteurs de forme et les BRDF^[6] donnant les échanges entre deux éléments de surface et calculer ainsi les échanges radiatifs dans une cavité. Dans ce type d'approche les ombres portées dans le cas d'une géométrie non convexe constituent une difficulté importante.

On peut ranger dans cette catégorie une méthode utilisée en infographie tridimensionnelle consistant à résoudre le problème de propagation à partir du point d'observation en remontant le trajet d'un certain nombre de rayons convergeant en ce point. C'est le lancer de rayons.

Méthode zonale

Hoyt Hottel en 1958^[20] a étendu le type de méthode précédent à un milieu absorbant en calculant toutes les géométries d'échange volume-volume ou surface-volume pour un problème en une dimension d'espace. Cette méthode appelée méthode zonale possède des désavantages qui ont dissuadé sa généralisation aux problèmes multidimensionnels :

• la construction du système pose le problème des parties cachées ;
• cette méthode couple deux à deux tous les éléments géométriques contenus dans une discrétisation de l'espace. Cela conduit donc à des matrices pleines dont la résolution est difficile et coûteuse.

Méthodes stochastiques

Ce type de méthode a été développé^[21] par Herman Kahn et Ted Harris (1948).

Dans les méthodes de type Monte-Carlo les phénomènes sont interprétés en termes probabilistes. Pour le déplacement ${\displaystyle \exp \left(-\int _{0}^{s}\kappa _{\nu }\left(\mathbf {r} -s'\mathbf {\Omega } ,t-{\frac {s'}{c}}\right)\mathrm {d} s'\right)}$ est la probabilité pour la particule de ne pas être absorbée sur le trajet ${\displaystyle (0,s)}$ et ${\displaystyle \kappa _{\nu }ds}$ la probabilité d'avoir une collision sur le trajet ${\displaystyle (s,s+\mathrm {d} s)}$. ${\displaystyle \kappa _{\nu }\exp \left(-\int _{0}^{s}\kappa _{\nu }\left(\mathbf {r} -s'\mathbf {\Omega } ,t-{\frac {s'}{c}}\right)\mathrm {d} s'\right)}$ est donc la densité de probabilité d'avoir une interaction après un trajet s.

À partir d'un espace maillé la méthode va donc consister à réaliser un grand nombre de pseudo-évènements avec diverses variables aléatoires en respectant les densités de probabilités :

• choix de la maille, de la fréquence et de la direction d'émission ;
• choix de la longueur de propagation ;
• choix du type d'interaction.

Après un grand nombre d'expériences de ce type, on effectue un bilan statistique dans chaque maille. Ce nombre N est généralement de plusieurs millions.

Cette méthode est utilisable dans toutes les situations, mais elle est coûteuse et limitée par le bruit statistique résiduel qui varie comme ${\displaystyle N^{-{\frac {1}{2}}}}$^[22]. Ce problème peut être minimisé en employant des techniques dites « biaisées » ou « non analogues »^[11].

Méthode PN

Cette méthode été introduite^[6] par James Jeans (1917)^[23].

Il est possible de rechercher la solution sous forme d'une série d'harmoniques sphériques dans le cas général ou de polynômes de Legendre ${\displaystyle P_{i}}$ dans les cas où la symétrie azimutale est respectée. Plaçons-nous dans ce dernier cas, on peut écrire l'approximation à l'ordre N

${\displaystyle L_{\nu }(\mathbf {r} ,t,\mu ,\nu )=\sum _{i=0}^{N}{\frac {2i+1}{2}}g_{i}(\mathbf {r} ,t,\nu )P_{i}(\mu )}$

En multipliant cette expression par ${\displaystyle P_{j}}$ et en tenant compte de l'orthogonalité des polynômes de Legendre on identifie les ${\displaystyle g_{i}}$ comme les moments

${\displaystyle g_{i}=\int _{-1}^{1}L_{\nu }P_{i}d\mu }$

En multipliant l'équation de transfert par chacun des ${\displaystyle P_{j}}$ et en tenant compte de la propriété d'orthogonalité des polynômes on obtient un système de N+1 équations pour N+2 inconnues ${\displaystyle g_{0},g_{1},...g_{N+1}}$. On fera donc une hypothèse pour clore le système. La plus simple consiste à imposer ${\displaystyle g_{N+1}=0}$.

On peut montrer que la série infinie est solution exacte de l'équation de transfert. Toutefois, cette propriété ne garantit pas que la série tronquée soit bonne : en particulier elle ne garantit pas la positivité de la solution qui peut être sensible au phénomène de Gibbs. Sauf problème particulier on obtient une bonne précision pour des valeurs de N comprises entre 10 et 100.

Un cas particulier est N=1. Il s'agit en fait d'une méthode très antérieure due à Eddington. En utilisant l'expression des deux premiers polynômes de Legendre et les quantités définies plus haut le développement s'écrit

${\displaystyle L_{\nu }={\frac {1}{4\pi }}\left(cE_{\nu }+3\mu M_{\nu }\right)}$

Le premier terme correspond à l'équilibre thermodynamique et le second à une correction d'ordre 1. Cette méthode est limitée à des milieux où l'écart à l'équilibre thermodynamique est faible. Pour ${\displaystyle |f_{\nu }|>{\frac {1}{3}}}$ elle conduit à des valeurs négatives de la luminance. De plus la vitesse de propagation calculée à partir de la matrice jacobienne est ${\displaystyle {\frac {c}{\sqrt {3}}}}$, ce qui est problématique pour un problème instationnaire.

On peut calculer la pression correspondante : dans ce calcul le second terme s'annule car impair en ${\displaystyle \mu }$ et on obtient un tenseur isotrope ${\displaystyle \mathbf {P} _{\nu }={\frac {E_{\nu }}{3}}{\mathsf {I}}}$.

Méthode SN

La méthode appelée « méthode aux ordonnées discrètes » ou méthode SN (S pour « segmenté »), introduite par Gian-Carlo Wick (1943)^[24] et Subrahmanyan Chandrasekhar (1944)^[25], consiste à discrétiser l'espace angulaire ${\displaystyle \theta ,\phi }$. Les N équations du transfert pour chacune des N directions ${\displaystyle \Omega _{i}}$ choisies sont couplées par les termes sources. Après résolution de ce système, on intègre en employant une quadrature

${\displaystyle \int _{4\pi }L_{\nu }d\Omega =\sum _{i=1}^{N}w_{i}L_{\nu }(\Omega _{i})}$

Dans le cas à symétrie azimutale, on utilise généralement comme directions les zéros de polynômes de Legendre. Les poids ${\displaystyle w_{i}}$ sont donnés par la méthode de Gauss ou celle de Gauss-Lobatto.

D'une façon générale, elle est très proche de la méthode ${\displaystyle P_{N}}$ dans la mesure où, pour des distributions angulaires régulières, elle conduit aux mêmes valeurs numériques de la solution aux points de quadrature. Le nombre de ces points est comme pour la méthode ${\displaystyle P_{N}}$ compris entre 10 et 100 pour le cas symétrique et peut atteindre plusieurs centaines dans le cas général.

Cette méthode ne peut pas prendre en compte un faisceau non aligné avec l'une des directions de discrétisation. Plus généralement, elle sera imprécise chaque fois que le problème contiendra de fortes anisotropies. Elle peut de plus être sensible au phénomène de Gibbs sur la distribution angulaire calculée.

Méthodes des moments

La méthode des moments consiste à multiplier l'équation de transfert par  ${\displaystyle \textstyle 1,\mathbf {\Omega } ,\mathbf {\Omega } \otimes \mathbf {\Omega } ,...}$  et à intégrer en angles. On trouve ainsi un système faisant apparaître les moments de la luminance définis plus haut et dans lequel la dépendance angulaire a disparu, ce qui constitue un gain considérable pour le calcul. Typiquement le gain est de plusieurs ordres de grandeur. En se limitant à l'ordre 1 on obtient pour un système à diffusion élastique

${\displaystyle {\begin{array}{lcl}{\frac {\partial E_{\nu }}{\partial t}}+\nabla \cdot \mathbf {M} _{\nu }&=&\kappa _{\nu }\left(4\pi S_{\nu }-cE_{\nu }\right)\\[0.6em]{\frac {\partial \mathbf {M} _{\nu }}{\partial t}}+c^{2}\nabla \cdot (E_{\nu }{\mathsf {D}}_{\nu })&=&-c\kappa _{\nu }^{tg}\mathbf {M} _{\nu }\end{array}}}$

On a fait apparaître un nouveau coefficient d'extinction  ${\displaystyle \textstyle \kappa _{\nu }^{tg}=\kappa _{\nu }^{t}-g_{\nu }\kappa _{\nu }^{d}}$  qui contient le premier moment de la distribution angulaire de diffusion

${\displaystyle g_{\nu }=\int _{4\pi }P_{1}{\mathcal {P}}_{\nu }d\Omega =2\pi \int _{-1}^{1}\mu {\mathcal {P}}_{\nu }d\Omega }$

Comme dans toute méthode aux moments ce système est incomplet puisque chaque équation sur un moment fait apparaître un moment d'ordre supérieur. Il faut donc pour le résoudre trouver une expression du tenseur d'Eddington, la plus complexe reliant celui-ci au flux et à l'énergie, seules quantités disponibles dans le système.

Un moyen très simple est de supposer le tenseur isotrope  ${\displaystyle \textstyle {\mathsf {D}}_{\nu }={\frac {1}{3}}{\mathsf {I}}}$  : c'est la méthode d'Eddington (voir ci-dessus méthode P₁). On obtient alors

${\displaystyle c^{2}\nabla \cdot (E_{\nu }{\mathsf {D}}_{\nu })={\frac {c^{2}}{3}}\nabla E_{\nu }}$

Cette méthode est peu précise et on cherchera une solution reliant le facteur d'Eddington au flux adimensionné (quantités définies ci-dessus). Ce type de méthode appelée « facteur d'Eddington variable » donne de bons résultats en général. Une méthode très générale et efficace a été introduite par G. N. Minerbo et pour cette raison appelée méthode M_N^[26]. Elle consiste à maximiser l'entropie du système, décrite par la statistique de Bose-Einstein. Ceci est à rapprocher de la théorie de l'information : la fermeture fait intervenir l'information minimale sur le système.

Le système d'équations aux moments a un caractère hyperbolique ce qui constitue un avantage car il peut être assez facilement couplé avec les équations du fluide, lesquelles sont de même nature. Cela constitue également un inconvénient dans la mesure où il peut apparaître dans la résolution des discontinuités de nature non physique qui disparaissent avec la montée à l'ordre M₂.

Diffusion

Si l'on écrit la seconde équation du système aux moments avec l'hypothèse d'un flux stationnaire et d'un tenseur isotrope (ce qui ne signifie pas nécessairement une luminance isotrope, voir ci-dessus l'approximation d'Eddington) on obtient un flux qui s'écrit comme un terme de diffusion^{[N 2]} analogue à la loi de Fick

${\displaystyle \mathbf {M} _{\nu }=-{\frac {c}{3\kappa _{\nu }^{tg}}}\nabla E_{\nu }}$

Cette expression reportée dans la première équation du système conduit à une équation analogue à l'équation de la chaleur. Dans l'expression générale, la dépendance angulaire n'apparaît plus, d'où un gain sur le calcul. Le caractère parabolique de cette équation conduit à une vitesse de propagation infinie. La solution ne sera donc pas valide aux temps courts d'un système instationnaire. De plus l'hypothèse du tenseur de pression isotrope n'est valide que pour des luminances peu anisotropes. Dans son domaine de validité, la méthode est extrêmement efficace et bénéficie de tous les développements théoriques et numériques qui ont été mis au point pour l'équation de la chaleur.

Le terme de droite de l'équation ci-dessus peut être multiplié par une fonction ad hoc baptisé « limiteur de flux » afin de retrouver une vitesse de propagation finie. Celle-ci n'est pas unique et ne permet généralement qu'une amélioration modeste du résultat.

Dans le cas d'un milieu à l'équilibre thermodynamique, on a vu que ${\displaystyle E_{\nu }={\frac {4\pi }{c}}L_{\nu }^{\circ }}$. Si donc on intègre l'équation ci-dessus en fréquence

${\displaystyle \mathbf {M} =-{\frac {4\pi }{3}}\int _{0}^{\infty }{\frac {1}{\kappa _{\nu }^{tg}}}{\frac {\partial L_{\nu }^{\circ }}{\partial T}}d\nu \nabla T\equiv -{\frac {4}{3}}{\frac {acT^{3}}{\kappa _{R}}}\nabla T\equiv -\lambda _{eq}\nabla T}$

On a introduit la moyenne de Rosseland^[27] (Svein Rosseland, 1924)^[28]

${\displaystyle \kappa _{R}={\frac {\int _{0}^{\infty }{\frac {\partial L_{\nu }^{\circ }}{\partial T}}d\nu }{\int _{0}^{\infty }{\frac {1}{\kappa _{\nu }^{tg}}}{\frac {\partial L_{\nu }^{\circ }}{\partial T}}d\nu }}={\frac {acT^{3}}{\pi \int _{0}^{\infty }{\frac {1}{\kappa _{\nu }^{tg}}}{\frac {\partial L_{\nu }^{\circ }}{\partial T}}d\nu }}}$

L'analogie avec l'équation de la chaleur est totale puisque l'on a pu définir une conductivité équivalente ${\displaystyle \lambda _{eq}}$.

Traitement de l'ensemble du spectre

Les spectres gazeux contiennent un fond continu (transition d'un électron d'un état lié au continuum, rayonnement continu de freinage) et des raies (transition entre états liés) lesquelles peuvent se compter en centaines de milliers, voire en millions. Le calcul raie par raie est exclu, sauf lorsque l'on veut effectuer un calcul de référence (tests de performance).

On va donc découper le spectre en bandes de fréquence ${\displaystyle (\nu ,\nu +\Delta \nu )}$ dans lesquelles on définit des moyennes par ${\displaystyle {\overline {f}}={\frac {1}{\Delta \nu }}\int _{\nu }^{\nu +\Delta \nu }fd\nu }$. Dans le cas avec émission à l'équilibre thermodynamique et sans diffusion on obtient en moyennant l'équation de transfert

${\displaystyle {\frac {1}{c}}{\frac {\partial {\overline {L_{\nu }}}}{\partial t}}+\mathbf {\Omega } \cdot \nabla {\overline {L_{\nu }}}+{\overline {\kappa _{\nu }L_{\nu }}}={\overline {\kappa _{\nu }L_{\nu }^{\circ }}}}$

Le terme source ne pose pas de problème. On peut l'écrire ${\displaystyle {\overline {\kappa _{\nu }L_{\nu }^{\circ }}}=\kappa _{P}aT^{4}}$, définissant ainsi la moyenne de Planck ${\displaystyle \kappa _{P}(T)}$ pour l'intervalle de fréquence considéré.

On va bien évidemment chercher à représenter le terme d'absorption sous la forme ${\displaystyle {\overline {\kappa _{\nu }L_{\nu }}}=\kappa _{m}{\overline {L_{\nu }}}}$ pour pouvoir se ramener aux méthodes de résolution connues. Mais ${\displaystyle \kappa _{\nu }}$ et ${\displaystyle L_{\nu }}$ sont a priori fortement corrélés, mais ceci est dépendant des termes source. Par suite ${\displaystyle {\overline {\kappa _{\nu }L_{\nu }}}}$ et ${\displaystyle {\overline {L_{\nu }}}}$ n'ont pas nécessairement la même dépendance angulaire et spatiale. Ceci implique que ${\displaystyle \kappa _{m}}$ va dépendre de ${\displaystyle s}$ pour ${\displaystyle \mathbf {\Omega } }$ donné.

Prenons l'exemple simple d'une bande dans laquelle un premier gaz absorbe dans la moitié de l'intervalle spectral choisi avec le coefficient ${\displaystyle \kappa _{1}}$, un second dans l'autre moitié avec le coefficient ${\displaystyle \kappa _{2}}$. Pour une intensité unité entrant sur un trajet s l'intensité sortante sera ${\displaystyle {\frac {1}{2}}\left(e^{-\kappa _{1}s}+e^{-\kappa _{2}s}\right)}$. On cherche une moyenne telle que l'intensité sortante soit ${\displaystyle e^{-\kappa _{m}s}}$. La solution de ce problème est

${\displaystyle \kappa _{m}=-{\frac {1}{s}}log\left[{\frac {1}{2}}\left(e^{-\kappa _{1}s}+e^{-\kappa _{2}s}\right)\right]}$

${\displaystyle \kappa _{m}}$ dépend de s et vaut ${\displaystyle {\frac {\kappa _{1}+\kappa _{2}}{2}}}$ quand ${\displaystyle s~\rightarrow ~0}$ et ${\displaystyle min(\kappa _{1},\kappa _{2})}$ lorsque ${\displaystyle s~\rightarrow ~\infty }$. La simple moyenne arithmétique constitue une bonne approximation pour les faibles trajets.

Si a présent on suppose que les deux gaz absorbent dans le même intervalle on voit que le problème a la même solution pour s petit mais n'en a aucune pour s grand : aucun coefficient d'absorption ne permet d'avoir une transmission 1/2 correspondant à la partie transparente. Dans ce cas le problème est mal posé.

 

De ce fait, l'approximation la plus simple ${\displaystyle \kappa _{m}={\overline {\kappa _{\nu }}}}$ conduira à des résultats médiocres sur le spectre calculé mais peut s'avérer suffisante si l'on ne s'intéresse qu'à l'aspect énergétique à condition de prendre un nombre suffisant de bandes : quelques dizaines à quelques milliers suivant la méthode de résolution et la précision recherchée.

Compte tenu de la complexité du problème des méthodes plus précises utilisent une connaissance a priori

• soit sur la forme du coefficient d'absorption, auquel cas on peut définir une approximation par l'intermédiaire d'un coefficient ${\displaystyle \kappa _{m}(s)}$ pour une direction donnée^[5],[6]. On ne peut donc utiliser ce type de méthode dans les problèmes multidimensionnels que lorsque la méthode de résolution résulte de la superposition de problèmes unidimensionnels (lancer de rayons, méthode ${\displaystyle S_{N}}$, etc.) ;
• soit parce que l'on connaît la forme de la luminance comme dans les méthodes de moments.

Notes

Références

Articles connexes

• Rayonnement thermique
• Diffusion des ondes
• Gaz de photons
• Structure stellaire
• Problème de Milne
• Fonction de phase de Henyey-Greenstein
• Approximation de Kubelka-Munk
• Méthode de Bhatnagar-Gross-Krook

Codes de calcul librement accessibles

• Génération et traitement d'image Blender ou [1] Mitsuba renderer
• Calcul en ligne de diffusion de Mie sur une sphère [2] Mie Scattering Calculator
• Transferts dans l'atmosphère: de nombreux codes sont décrits dans l'article de Wikipédia Atmospheric radiative transfer codes
• Codes Monte-Carlo pour le dépôt de particules dans la matière [3] Geant4, [4], Penelope
• Code général hydrodynamique-rayonnement pour l'astrophysique [5] 3D parallel code for hydrodynamics, MHD, radiative transfer and gravity
• Code MATLAB pour les méthodes P_N ou SP_N, (en) Benjamin Seibold, « StaRMAP », sur Université Temple

Bases de données librement accessibles

• Émission et absorption dans un milieu gazeux [6] Line-by-line radiative code SPARTAN
• Base de données pour les calculs atmosphériques ou la combustion [7] The HITRAN Database
• Base de données pour les calculs atmosphériques [8] GEISA : spectroscopic database
• Base de données pour l'astrophysique [9] TIPbase
• Bases de données pour la physique des plasmas et l'astrophysique [10] Atomic and Molecular Spectroscopic Data
• Répertoire de diverses bases [11] Plasma Laboratory - Weizmann Institute of Science

• Portail de la physique
• Portail de l’optique
• Portail des sciences de la Terre et de l’Univers
• Portail de l’astronomie