Produit de convolution

En mathématiques, le produit de convolution est un opérateur bilinéaire et un produit commutatif, généralement noté « ∗ », qui, à deux fonctions f et g sur un même domaine infini, fait correspondre une autre fonction « f ∗ g » sur ce domaine, qui en tout point de celui-ci est égale à l'intégrale sur l'entièreté du domaine (ou la somme si celui-ci est discret) d'une des deux fonctions autour de ce point, pondérée par l'autre fonction autour de l'origine — les deux fonctions étant parcourues en sens contraire l'une de l'autre (nécessaire pour garantir la commutativité).

Le produit de convolution généralise l'idée de moyenne glissante et est la représentation mathématique de la notion de filtre linéaire. Il s'applique aussi bien à des données temporelles (en traitement du signal par exemple) qu'à des données spatiales (en traitement d'image). En statistique, on utilise une formule très voisine pour définir la corrélation croisée.

Définition du produit de convolution

Le produit de convolution de deux fonctions réelles ou complexes f et g, est une autre fonction, qui se note généralement ${\displaystyle f\ast g}$ et qui est définie par :

${\displaystyle (f\ast g)(x)=\int _{-\infty }^{+\infty }f(x-t)g(t)\,\mathrm {d} t=\int _{-\infty }^{+\infty }f(t)g(x-t)\,\mathrm {d} t}$

Parfois l'opération ∗ s'appelle loi de convolution et ${\displaystyle f\ast g}$ s'appelle la convoluée^[1].

Pour des suites (en remplaçant la mesure de Lebesgue par la mesure de comptage) :

${\displaystyle (f\ast g)(n)=\sum _{m=-\infty }^{\infty }{f(n-m)g(m)}=\sum _{m=-\infty }^{\infty }{f(m)g(n-m)}}$.

Lorsqu'il s'agit de séries, on parle de produit de Cauchy (mais dans ce qui suit, nous n'utiliserons que la version « continue »).

On peut considérer cette formule comme une généralisation de l'idée de moyenne mobile.

Pour que cette définition ait un sens, il faut que f et g satisfassent certaines hypothèses ; par exemple, si ces deux fonctions sont intégrables au sens de Lebesgue (c'est-à-dire qu'elles sont mesurables et que l'intégrale de leur module est finie), leur produit de convolution est défini pour presque tout x et est lui-même intégrable. Plus généralement, si f ∈ L^p et g ∈ L^q et ${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}=1+{\frac {1}{r}}}$ avec ${\displaystyle p,q,r\in [1,+\infty ]}$, alors f ∗ g ∈ L^r : cf. « Inégalité de Young pour la convolution ».

Propriétés du produit de convolution

Propriétés algébriques

Le produit de convolution est bilinéaire, associatif et commutatif :

${\displaystyle f\ast (g+\lambda h)=(f\ast g)+\lambda (f\ast h)}$ (pour tout scalaire λ) ;

${\displaystyle (f\ast g)\ast h=f\ast (g\ast h)}$ ;

${\displaystyle f\ast g=g\ast f}$.

Pseudo-anneau

L'ensemble des fonctions intégrables muni de l'addition et du produit de convolution forme donc un pseudo-anneau, c'est-à-dire un anneau non unitaire. En effet, si cet anneau était unitaire, l'élément unité δ devrait vérifier (pour tout x et toute fonction f) :

${\displaystyle f(x)=\int _{-\infty }^{+\infty }f(t)\delta (x-t)\,\mathrm {d} t}$.

On vérifie aisément que ce n'est possible que si δ est la distribution de Dirac… qui n'est pas une fonction.

Le cadre naturel pour une bonne généralisation du produit de convolution est celui de la théorie des distributions, mais il n'est pas abordé dans cet article. On trouvera dans l'article consacré aux distributions une définition précise du produit de convolution dans ce cas, ainsi qu'une étude de ses principales propriétés.

Compatibilité avec les translations

Le produit de convolution est compatible avec les translations temporelles. Si l'on note τ_h la translation sur les fonctions définie par

${\displaystyle (\tau _{h}f)(x)=f(x-h)}$,

alors

${\displaystyle (\tau _{h}f)\ast g=\tau _{h}(f\ast g).}$

Dans le cadre plus large de la convolution des mesures,

${\displaystyle \tau _{h}f=\delta _{h}\ast f}$,

où δ_h désigne la masse de Dirac en h, et la compatibilité avec les translations n'est qu'une conséquence immédiate de l'associativité du produit de convolution des mesures :

${\displaystyle (\tau _{h}f)\ast g=(\delta _{h}\ast f)\ast g=\delta _{h}\ast (f\ast g)=\tau _{h}(f\ast g).}$

Cette propriété doit par ailleurs être rapprochée des applications des produits de convolution au filtrage.

Parité

La convolution suit la règle des signes pour la parité des fonctions :

f ∗ g est paire (resp. impaire) si f et g sont de même parité (resp. de parités contraires).

Cette propriété combinée avec l'invariance sous translation permet de prouver que le produit de convolution par une fonction paire préserve les symétries axiales des fonctions :

Si g est paire et si f (x–h)=f(–x–h) alors (f ∗ g)(x–h)=(f ∗ g)(–x–h).

Intégration d'un produit de convolution

On a (en appliquant le théorème de Fubini) la formule : ${\displaystyle \int _{-\infty }^{+\infty }(f\ast g)(t)\,\mathrm {d} t=\left(\int _{-\infty }^{+\infty }f(t)\,\mathrm {d} t\right)\left(\int _{-\infty }^{+\infty }g(t)\,\mathrm {d} t\right).}$

Dérivation

Dans le cas d'une seule variable, si f (par exemple) est de classe C¹ et si f, f ' et g appartiennent à L¹ alors

${\displaystyle (f*g)'=f'*g}$.

Plus généralement dans les cas de fonctions de plusieurs variables on a

${\displaystyle {\frac {\partial }{\partial x_{i}}}(f*g)={\frac {\partial f}{\partial x_{i}}}*g}$.

Produit de convolution et transformée de Fourier

La transformée de Fourier d'un produit de convolution s'obtient par multiplication des transformées de Fourier des fonctions :

• si f et g sont intégrables alors${\displaystyle {\mathcal {F}}(f\ast g)={\mathcal {F}}(f){\mathcal {F}}(g)~;}$
• si f est intégrable et si g est de carré intégrable, on a aussi

${\displaystyle {\mathcal {F}}(f\ast g)={\mathcal {F}}(f){\mathcal {F}}(g){\text{ donc }}f\ast g={\mathcal {F}}^{-1}\left({\mathcal {F}}(f){\mathcal {F}}(g)\right)~;}$

• si f et g sont de carré intégrable alors${\displaystyle f\ast g={\mathcal {F}}^{-1}\left({\mathcal {F}}(f){\mathcal {F}}(g)\right)}$

où ${\displaystyle {\mathcal {F}}}$ désigne la transformation de Fourier et ${\displaystyle {\mathcal {F}}^{-1}}$ la transformation de Fourier inverse (« théorème de convolution »).

Ces formules se restreignent à l'espace de Schwartz, puis s'étendent partiellement à la transformation de Fourier pour les distributions tempérées, appliquée par exemple à la convoluée d'une distribution tempérée par une distribution à support compact. Plus généralement, si S et T sont deux distributions tempérées dont l'une est un convoleur, alors leurs transformées de Fourier sont des distributions tempérées dont l'une est un multiplieur, et elles vérifient :${\displaystyle {\mathcal {F}}(S\ast T)={\mathcal {F}}(S){\mathcal {F}}(T){\text{ donc }}S\ast T={\mathcal {F}}^{-1}\left({\mathcal {F}}(S){\mathcal {F}}(T)\right).}$

Dans ce cadre, la distribution de Dirac (convoleur neutre) et la fonction constante 1 (multiplieur neutre) sont deux distributions tempérées (paires) transformées de Fourier l'une de l'autre.

L'intérêt principal du calcul du produit de convolution par transformées de Fourier est que ces opérations sont moins coûteuses en temps pour un ordinateur que le calcul direct de l'intégrale.

Utilisation du produit de convolution

• Le produit de convolution est utilisé dans le traitement du signal, lorsque l'on utilise des filtres (passe-bas, passe-haut, passe-bande). Si l'on a un signal entrant e(t) et un élément filtrant ayant une fonction de transfert h(t) alors le signal de sortie s(t) sera la convolution de ces deux fonctions :${\displaystyle s=e\ast h}$ (produit de convolution) et S(f)=E(f)H(f) (produit simple de deux fonctions) où E(f), S(f) et H(f) sont les transformées de Fourier des fonctions du temps e(t) , s(t) et h(t).
• En audio numérique, et particulièrement dans le mixage musical ou audiovisuel, des logiciels de réverbération à convolution existent. Ils effectuent, dans le domaine fréquentiel, un produit de convolution entre le signal audio entrant et une réponse impulsionnelle sélectionnée par l'utilisateur. Ces logiciels disposent d'une banque de réponses impulsionnelles correspondant à divers environnements dont on souhaite reproduire la réverbération sonore (pièces, grottes, églises, ...), réponses obtenues en enregistrant la réverbération du lieu à un signal source donné.
• En cristallographie, le théorème de convolution est utilisé dans les méthodes directes pour déterminer la phase des facteurs de structure lors de la détermination d'une structure cristalline.
• En probabilité, la densité de probabilité de la somme de deux variables aléatoires réelles indépendantes (à densité) est le produit de convolution des densités de probabilité de ces deux variables indépendantes, comme on le voit à l'aide d'un changement de variables^[2].
• Une autre utilisation des produits de convolution se situe dans le domaine de la mécanique quantique, où l'on réalise des produits de convolution à partir des fonctions d'onde bra et ket.
• De manière générale, on peut écrire les équations différentielles linéaires correspondant à de nombreux problèmes physiques sous la forme du produit de convolution d'un opérateur par une fonction décrivant le système. On peut alors résoudre de manière générique le problème en déterminant l'inverse de convolution de l'opérateur (appelé fonction de Green). Joseph Fourier a été à l'origine de cette méthode lorsqu'il a cherché à résoudre l'équation de la chaleur. Sa formulation moderne a dû attendre l'arrivée de la théorie des distributions introduite par Laurent Schwartz.
• Le produit de convolution se généralise à de nombreuses algèbres d'un groupe, par exemple aux algèbres d'un groupe fini. Si de plus le groupe est abélien, alors la théorie de l'analyse harmonique sur un groupe abélien fini permet d'établir tous les résultats classiques du produit de convolution.
• En apprentissage profond, des opérateurs de convolution constituent les banques de filtres des réseaux neuronaux convolutifs pour la vision par ordinateur ou le traitement automatique du langage naturel.

Produit de convolution de mesures

Convolution de mesures sur la droite réelle

Par extension, on peut définir le produit de convolution de deux mesures sur ${\displaystyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} )),}$ avec l'interprétation probabiliste suivante : lorsque les lois de probabilité μ et ν de deux variables aléatoires réelles indépendantes n'ont pas toutes les deux des densités par rapport à la mesure de Lebesgue, la loi de leur somme est le produit de convolution de μ par ν, noté μ ∗ ν et défini, pour toute partie borélienne A de ${\displaystyle \mathbb {R} ,}$ par

${\displaystyle \mu \ast \nu (A)=\int _{\mathbb {R} ^{2}}\ 1_{A}(x+y)\,\mu (\mathrm {d} x)\,\nu (\mathrm {d} y).}$

L'intégrale d'une fonction θ par rapport à la mesure μ ∗ ν est donnée par

${\displaystyle \int _{\mathbb {R} }\ \theta (s)\,(\mu \ast \nu )(\mathrm {d} s)\ =\ \int _{\mathbb {R} ^{2}}\ \theta (x+y)\,\mu (\mathrm {d} x)\,\nu (\mathrm {d} y).}$

Le produit de convolution μ ∗ ν est la mesure image par la fonction φ, définie sur ${\displaystyle \mathbb {R} ^{2}}$ par φ(x, y) = x + y, de la mesure produit μ ⊗ ν. En particulier, si μ et ν ont toutes les deux des densités, respectivement f et g, par rapport à la mesure de Lebesgue, alors μ ∗ ν a aussi une densité par rapport à la mesure de Lebesgue, et une de ses densités est f ∗ g.

Convolution de mesures sur un groupe commutatif

Cette définition du produit de convolution peut être étendue à un groupe topologique commutatif (G,⊕) muni de sa tribu borélienne, de manière immédiate : pour toute partie borélienne A de G,

${\displaystyle \mu \ast \nu (A)=\int _{G^{2}}\ 1_{A}(x\oplus y)\,\mu (\mathrm {d} x)\,\nu (\mathrm {d} y).}$

L'intégrale d'une fonction θ par rapport à la mesure μ ∗ ν est donnée par

${\displaystyle \int _{G}\ \theta (s)\,(\mu \ast \nu )(\mathrm {d} s)\ =\ \int _{G^{2}}\ \theta (x\oplus y)\,\mu (\mathrm {d} x)\,\nu (\mathrm {d} y).}$

La notion de mesure de Haar du groupe G s'écrit alors en termes de produit de convolution : μ est une mesure de Haar de G si et seulement si, pour tout élément g de G,

${\displaystyle \delta _{g}\ast \mu =\mu .}$

Si le groupe n'est pas commutatif, on peut quand même définir un produit de convolution en précisant convolution à gauche ou à droite.

Plus généralement, on peut définir un produit de convolution pour une action de groupe. Soit G un groupe mesurable agissant sur un espace mesurable K, d'action notée . et soient μ une mesure sur G et ν une mesure sur K. On définit le produit de convolution par la formule

${\displaystyle \mu *\nu (A)=\int _{K}\int _{G}{\mathsf {1}}_{A}(g.x)\,\mu (\mathrm {d} g)\,\nu (\mathrm {d} x)}$ où A est une partie mesurable de K.

C'est une mesure sur K. Si K = G et si l'action est la multiplication (ou la multiplication à gauche ou à droite si le groupe n'est pas commutatif), alors on retrouve le produit de convolution sur les groupes décrit plus haut.

Approche vulgarisée

Convolution avec un dirac

La manière la plus simple de représenter le produit de convolution consiste à considérer la fonction δ de Dirac δ_a(x) ; cette « fonction » vaut 0 si x ≠ a et son intégrale vaut 1. Ceci peut paraître contre-intuitif, mais on peut l'imaginer comme la limite d'une suite de fonctions, des courbes en cloche ou des rectangles ayant toutes la même surface 1, mais de plus en plus fines (donc de plus en plus hautes) ; lorsque la largeur des courbes tend vers 0, sa hauteur tend vers +∞, mais la surface reste égale à 1. Pour des raisons pratiques, on représente souvent le dirac comme un bâton placé en a et de hauteur 1.

Le produit de convolution par un dirac δ_a correspond à une translation de la fonction initiale d'une valeur de a

${\displaystyle f\ast \delta _{a}(x)=f(x-a)}$

Produit de convolution d'une fonction par le dirac en a

En particulier pour a = 0, on voit que δ₀ laisse invariante la fonction ${\displaystyle f}$ : ${\displaystyle f\ast \delta _{0}(x)=f(x-0)}$. Ainsi δ₀ est l'élément neutre du produit de convolution

Convolution avec une somme pondérée de deux diracs

Si l'on considère maintenant le produit de convolution par une somme pondérée de deux diracs (α δ_a + β δ_b), on obtient la superposition de deux courbes translatées.

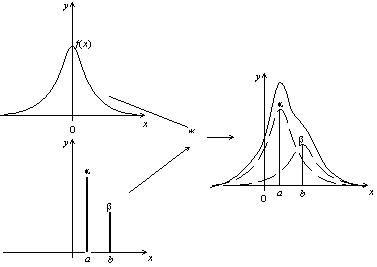
Produit de convolution d'une fonction par une somme pondérée de deux diracs

Convolution avec une fonction porte

Considérons maintenant une fonction porte P_a,b ; c'est une fonction qui vaut 1/(b-a) entre a et b, et 0 ailleurs (son intégrale vaut 1). Cette fonction peut être vue comme une succession de diracs. La convolution de f par P_a,b va donc s'obtenir en faisant glisser f sur l'intervalle [a;b]. On obtient un « élargissement » de f.

Produit de convolution d'une fonction par une fonction porte

Si l'on considère maintenant une fonction quelconque g, on peut voir g comme une succession de diracs pondérés par la valeur de g au point considéré. Le produit de convolution de f par g s'obtient donc en faisant glisser la fonction f et en la dilatant selon la valeur de g.

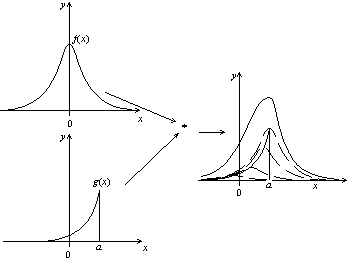
Produit de convolution d'une fonction par une fonction quelconque

Le produit de convolution et le filtrage

Le produit de convolution est lié à la notion de filtrage sous deux conditions, à savoir la linéarité et l'indépendance du filtre vis-à-vis du temps (système invariant). À partir de ces deux conditions, l'opérateur de convolution peut être construit. La convolution correspond à la réponse du filtre à une entrée donnée (notée e(t) ). Le filtre est entièrement caractérisé par sa réponse impulsionnelle h(t). Mise en équation, la réponse du filtre est s(t) = {h ∗ e}(t).

La construction de l'opérateur de convolution s'élabore de la manière suivante. Tout d'abord, on s'intéresse aux deux conditions imposées sur le filtre. On note f (e) le filtrage réalisé par le filtre sur l'entrée e. La linéarité du filtre implique que :

${\displaystyle f(\lambda e)=\lambda f(e)}$

${\displaystyle f(e_{1}+e_{2})=f(e_{1})+f(e_{2})}$

On peut noter que la réponse du filtre à un signal nul est nulle. L'indépendance du temps se résume par :

${\displaystyle f(e^{d})=(f(e))^{d}}$

où e^d est le signal e retardé de la quantité d.

À partir de là, on peut construire la réponse du filtre linéaire et indépendant du temps à l'entrée e(t) . En effet, comme le filtre est linéaire, on peut décomposer le signal e(t) en parties indépendantes, à l'aide d'un ensemble de signaux e_i avec des supports disjoints compacts de telle sorte que ${\displaystyle e(t)=\Sigma _{i}e_{i}(t)}$. On injecte chaque partie du signal dans le filtre puis l'on somme les différentes réponses. Ainsi le filtrage donnera : ${\displaystyle f(e)=\Sigma _{i}f(e_{i})}$. Cette décomposition temporelle de e(t) peut s'effectuer de manière récursive sur les signaux e_i(τ). À la fin, on obtient une suite de signaux dont le support se résume à un point. Ces signaux, élémentaires parce que non décomposables temporellement, correspondent chacun d'entre eux à la distribution de Dirac δ(t–τ) centrée en τ avec une amplitude e(τ), l'impulsion s'écrit δ(t–τ)e(τ). Il suffit de sommer toutes les impulsions suivant la variable τ pour obtenir le signal e(t) :

${\displaystyle e(t)=\int \delta (t-\tau )e(\tau )\,\mathrm {d} \tau }$

On applique l'opération de filtrage sur e(t) . Comme le filtre est linéaire et indépendant du temps, nous avons :

${\displaystyle {\begin{aligned}f(e)&=\int f(\delta (t-\tau )e(\tau ))\,\mathrm {d} \tau \\&=\int e(\tau )f(\delta (t-\tau ))\,\mathrm {d} \tau &{\text{(linéarité)}}\\&=\int e(\tau )(f\circ \delta )(t-\tau )\,\mathrm {d} \tau &{\text{(indépendance du temps).}}\end{aligned}}}$

La réponse du filtre f à l'impulsion δ(t) est nommée la réponse impulsionnelle du filtre h(t). Finalement on a :

${\displaystyle f(e)=\int e(\tau )h(t-\tau )\,\mathrm {d} \tau }$

qui n'est autre que le produit de convolution.

En conclusion : si le filtre est linéaire et indépendant du temps, alors il est entièrement caractérisé par sa réponse h(t) et la réponse du filtre à l'entrée e(t) est donnée par l'opérateur de convolution.

Autre conclusion fondamentale des filtres linéaires et indépendants du temps : si l'on entre un signal e(t)=e^{2 π j f t}, le signal de sortie sera :

${\displaystyle {\begin{aligned}s(t)&=\int \mathrm {e} ^{2\pi \jmath f\tau }h(t-\tau )\,\mathrm {d} \tau \\&=\int \mathrm {e} ^{2\pi \jmath f(t-\tau )}h(\tau )\,\mathrm {d} \tau \\&=\mathrm {e} ^{2\pi \jmath ft}\int \mathrm {e} ^{-2\pi \jmath f\tau }h(\tau )\,\mathrm {d} \tau \\&=\mathrm {e} ^{2\pi \jmath ft}H(f).\end{aligned}}}$

Le signal s(t) sera aussi un signal de la forme e^{2 π j f t} au facteur H(f) près. Ce facteur n'est autre que la transformée de Fourier de h(t).

Notes et références

Voir aussi

Articles connexes

• Approximation de l'unité
• Convolution de Dirichlet
• Déconvolution
• Dualité de Pontriaguine
• Fenêtrage
• Intégrale paramétrique

Bibliographie

Marc Briane et Gilles Pagès, Théorie de l'intégration : convolution et transformée de Fourier, Paris, Vuibert, 2012, 365 p. (ISBN 978-2-311-00738-1)

Liens externes

• (en) Animation de la Johns Hopkins University qui explique la convolution de façon graphique
• Viva la Convolution : application de la convolution à l'acoustique

• Portail de l'analyse