Quadripôle

Cet article concerne le quadripôle (ou quadrupôle) en électrocinétique. Pour le quadrupôle en électrostatique, voir Quadrupôle.

En électrocinétique, un quadripôle (ou quadrupôle) est un élément de modèle d'un circuit électrique dans lequel on le considère comme un bloc avec deux connexions d'entrée et deux de sortie. On étudie le transfert des grandeurs électriques, tension et courant, entre ces deux dipôles caractérisés par une impédance, en fonction du temps.

Quand l'étude du quadripôle concerne un signal électrique, la grandeur en entrée et en sortie peut être différente (tension, courant). L'apport éventuel d'énergie au circuit, qu'on dit alors actif, ne fait pas partie du modèle. On doit les premières études sur les quadripôles au mathématicien allemand Franz Breisig, dans les années 1920.

L'analogie électro-mécanique permet d'utiliser le formalisme des quadripôles pour des transducteurs ou des systèmes mécaniques ou électro-mécaniques.

Généralités

Définitions

Un quadripôle est un composant ou circuit électronique envisagé comme une boîte noire présentant deux ports électriques^[1]. On s'intéresse au courant et à la tension sur chacun des ports, avec les conventions figurées ci-dessous : les courants entrants dans le quadripôle au pôle positif de la tension sont notés positivement.

désignation des grandeurs
grandeur physique	entrée	sortie
courant	$I_{1}$ ou $I_{e}$	$I_{2}$ ou $I_{s}$
tension	$V_{1}$ ou $U_{e}$	$V_{2}$ ou $U_{s}$

Cette convention rend l'entrée et la sortie symétriques. Le quadripôle est déterminé par deux équations caractéristiques qui permettent, connaissant celles de dispositifs qui lui sont raccordés, de calculer les valeurs d'entrée et de sortie^[2].

Fonction de transfert

La fonction de transfert ${\underline {T}}$ d’un quadripôle linéaire en régime alternatif sinusoïdal possède les propriétés suivantes :

– C'est un nombre complexe ${\underline {T}}={\underline {T}}(j\omega )$ . Ce nombre dépend de la fréquence et de la charge placée en sortie.

– $|{\underline {T}}|$ , parfois simplement noté $T$ , est le rapport entre les valeurs efficaces du signal de sortie et du signal d'entrée.

– $\arg {({\underline {T}})}$ est la différence de phase (ou déphasage) du signal de sortie par rapport au signal d'entrée.

Coefficients d'amplification

Les coefficients d'amplification sont des fonctions de transfert particulières.

Coefficient d'amplification en tension : $T=A_{v}={\frac {U_{s}}{U_{e}}}$
Coefficient d'amplification en courant : $T=A_{i}={\frac {I_{s}}{I_{e}}}$

coefficient d'amplification en puissance, bien que ce ne soit pas un rapport de nombres complexes associés à des signaux :

$A_{p}={\frac {U_{s}I_{s}\cos {(\varphi _{s})}}{U_{e}I_{e}\cos {(\varphi _{e})}}}$ avec $\varphi _{s}$ (respectivement $\varphi _{e}$ ) le déphasage de $U_{s}$ par rapport à $I_{s}$ (respectivement de $U_{e}$ par rapport à $I_{e}$ ).

Ces coefficients dépendent en général de la fréquence et de la charge en sortie.

Gains

Comme les modules de ces coefficients peuvent varier de façon importante lorsque la fréquence varie, on utilise une autre grandeur qui "tasse" ces variations.

Gain en tension : $G_{V}=20\log \left({\frac {U_{S}}{U_{E}}}\right)$

Gain en courant : $G_{I}=20\log \left({\frac {I_{S}}{I_{E}}}\right)$
Gain en puissance : $G_{P}=10\log \left({\frac {P_{S}}{P_{E}}}\right)$

Les gains s'expriment en décibels.

Lorsque T est multiplié par 10, G=20logT augmente de 20 dB ;
Le gain devient négatif si T<1.
Lorsque Av double, Gv augmente de 6 dB.

Paramétrage d'un quadripôle linéaire

On représente les quadripôles sous forme de matrices reliant les courants et tensions, dont les termes dépendent éventuellement de la fréquence. On peut construire ces matrices de différentes façons : elles sont toutes équivalentes, mais la construction la plus pratique dépendra des problèmes à résoudre^[3].

Paramétrage transfert ou cascade

On exprime les données de gauche en fonction de celles de droite. Les termes sont notés ABCD, $T_{ij}$ ou $a_{ij}$ , selon les conventions : ${V_{1} \choose I_{1}}={\begin{pmatrix}A&B\\C&D\end{pmatrix}}{V_{2} \choose -I_{2}}$ ,

Ou à l'inverse, on écrit les termes de droite en fonction des termes de gauche. C'est la matrice A'B'C'D', $T'_{ij}$ ou $b_{ij}$ , inverse de la précédente :

${V_{2} \choose -I_{2}}={\begin{pmatrix}A'&B'\\C'&D'\end{pmatrix}}{V_{1} \choose I_{1}}$ ,

${\begin{pmatrix}A&B\\C&D\end{pmatrix}}{\begin{pmatrix}A'&B'\\C'&D'\end{pmatrix}}={\begin{pmatrix}1&0\\0&1\end{pmatrix}}$

A et D sont adimensionnels, B est en ohms, et C en siemens. Ce paramétrage est adapté au chaînage des quadripôles. Le courant de sortie du premier quadripôle est l'opposé du courant d'entrée du quadripôle suivant, d'où le signe « - ».

Paramétrage en impédances

On exprime les tensions en fonction des courants : ${V_{1} \choose V_{2}}={\begin{pmatrix}Z_{11}&Z_{12}\\Z_{21}&Z_{22}\end{pmatrix}}{I_{1} \choose I_{2}}$ ,avec : $Z_{11}={V_{1} \over I_{1}}{\bigg |}_{I_{2}=0}\qquad Z_{12}={V_{1} \over I_{2}}{\bigg |}_{I_{1}=0}$ et $Z_{21}={V_{2} \over I_{1}}{\bigg |}_{I_{2}=0}\qquad Z_{22}={V_{2} \over I_{2}}{\bigg |}_{I_{1}=0}$

On appelle $Z_{11}$ l'impédance d'entrée du quadripôle ; $Z_{12}$ l'impédance de transfert inverse du quadripôle ; $Z_{21}$ l'impédance de transfert du quadripôle ; $Z_{22}$ l'impédance de sortie du quadripôle. Tous ces termes sont en ohms.

Paramétrage en admittances

On exprime les courants en fonction des tensions : ${I_{1} \choose I_{2}}={\begin{pmatrix}Y_{11}&Y_{12}\\Y_{21}&Y_{22}\end{pmatrix}}{V_{1} \choose V_{2}}$ ,avec : $Y_{11}={I_{1} \over V_{1}}{\bigg |}_{V_{2}=0}\qquad Y_{12}={I_{1} \over V_{2}}{\bigg |}_{V_{1}=0}$ et $Y_{21}={I_{2} \over V_{1}}{\bigg |}_{V_{2}=0}\qquad Y_{22}={I_{2} \over V_{2}}{\bigg |}_{V_{1}=0}$

On appelle $Y_{11}$ l'admittance d'entrée du quadripôle ; $Y_{12}$ l'admittance de transfert inverse du quadripôle ; $Y_{21}$ l'admittance de transfert du quadripôle ; $Y_{22}$ l'admittance de sortie du quadripôle. Tous les termes sont des admittances, donc exprimés en siemens.

Paramétrage hybride

Article détaillé : Paramètre hybride.

Ces relations sont utiles lors de l'étude des transistors. (voir #Quadripôles_passifs)

${V_{1} \choose I_{2}}={\begin{pmatrix}H_{11}&H_{12}\\H_{21}&H_{22}\end{pmatrix}}{I_{1} \choose V_{2}}$ , avec : $H_{11}={V_{1} \over I_{1}}{\bigg |}_{V_{2}=0}\qquad H_{12}={V_{1} \over V_{2}}{\bigg |}_{I_{1}=0}$ et $H_{21}={I_{2} \over I_{1}}{\bigg |}_{V_{2}=0}\qquad H_{22}={I_{2} \over V_{2}}{\bigg |}_{I_{1}=0}$

On peut noter que $H_{11}=1/Y_{11}$ et que $H_{22}=1/Z_{22}$ .

On appelle $H_{11}$ l'impédance d'entrée du quadripôle (ohms); $H_{12}$ le gain inverse en tension du quadripôle (adimensionnel); $H_{21}$ le gain en courant de transfert du quadripôle (adimensionnel), $H_{22}$ l'admittance de sortie du quadripôle (siemens).

Le calcul matriciel s'adapte très bien aux quadripôles et permet d'obtenir les fonctions de transferts des circuits électroniques quand d'autres méthodes s'égarent dans un formalisme abscons, source d'erreurs et de pertes de temps.

Paramétrage hybrides inverse

Les relations hybrides inverse sont très peu utilisées, mais elles existent.

${I_{1} \choose V_{2}}={\begin{pmatrix}G_{11}&G_{12}\\G_{21}&G_{22}\end{pmatrix}}{V_{1} \choose I_{2}}$ , avec : $G_{11}={I_{1} \over V_{1}}{\bigg |}_{I_{2}=0}\qquad G_{12}={I_{1} \over I_{2}}{\bigg |}_{V_{1}=0}$ et $G_{21}={V_{2} \over V_{1}}{\bigg |}_{I_{2}=0}\qquad G_{22}={V_{2} \over I_{2}}{\bigg |}_{V_{1}=0}$

Conversion des matrices

Les paramétrages donnés ci-dessous sont équivalents : des conversions permettent de passer de l'un à l'autre. Néanmoins, certains quadripôles ne peuvent être décrits dans certains paramétrage, par exemple si les formules de conversion impliquent une division par zéro. $\Delta$ représente le déterminant de la matrice.

Conversion entre les différentes matrices^[4]
	Paramètres ABCD	Paramètres Z	Paramètres Y	Paramètres H
Matrice de transfert ABCD	${\begin{bmatrix}A&B\\C&D\end{bmatrix}}$	${\begin{bmatrix}{\frac {Z_{11}}{Z_{21}}}&{\frac {\Delta Z}{Z_{21}}}\\{\frac {1}{Z_{21}}}&{\frac {Z_{22}}{Z_{21}}}\end{bmatrix}}$	${\begin{bmatrix}-{\frac {Y_{22}}{Y_{21}}}&-{\frac {1}{Y_{21}}}\\-{\frac {\Delta Y}{Y_{21}}}&-{\frac {Y_{11}}{Y_{21}}}\end{bmatrix}}$	${\begin{bmatrix}-{\frac {\Delta H}{H_{21}}}&-{\frac {H_{11}}{H_{21}}}\\-{\frac {H_{22}}{H_{21}}}&-{\frac {1}{H_{21}}}\end{bmatrix}}$
Matrice d'impédance Z	${\begin{bmatrix}{\frac {A}{C}}&{\frac {\Delta (ABCD)}{C}}\\{\frac {1}{C}}&{\frac {D}{C}}\end{bmatrix}}$	${\begin{bmatrix}Z_{11}&Z_{12}\\Z_{21}&Z_{22}\end{bmatrix}}$	${\begin{bmatrix}{\frac {Y_{22}}{\Delta Y}}&-{\frac {Y_{12}}{\Delta Y}}\\-{\frac {Y_{21}}{\Delta Y}}&{\frac {Y_{11}}{\Delta Y}}\end{bmatrix}}$	${\begin{bmatrix}{\frac {\Delta H}{H_{22}}}&{\frac {H_{12}}{H_{22}}}\\-{\frac {H_{21}}{H_{22}}}&{\frac {1}{H_{22}}}\end{bmatrix}}$
Matrice d'admittance Y	${\begin{bmatrix}{\frac {D}{B}}&-{\frac {\Delta (ABCD)}{B}}\\-{\frac {1}{B}}&{\frac {A}{B}}\end{bmatrix}}$	${\begin{bmatrix}{\frac {Z_{22}}{\Delta Z}}&-{\frac {Z_{12}}{\Delta Z}}\\-{\frac {Z_{21}}{\Delta Z}}&{\frac {Z_{11}}{\Delta Z}}\end{bmatrix}}$	${\begin{bmatrix}Y_{11}&Y_{12}\\Y_{21}&Y_{22}\end{bmatrix}}$	${\begin{bmatrix}{\frac {1}{H_{11}}}&-{\frac {H_{12}}{H_{11}}}\\{\frac {H_{21}}{H_{11}}}&{\frac {\Delta H}{H_{11}}}\end{bmatrix}}$
Matrice hybride H	${\begin{bmatrix}{\frac {B}{D}}&{\frac {\Delta (ABCD)}{D}}\\-{\frac {1}{D}}&{\frac {C}{D}}\end{bmatrix}}$	${\begin{bmatrix}{\frac {\Delta Z}{Z_{22}}}&{\frac {Z_{12}}{Z_{22}}}\\-{\frac {Z_{21}}{Z_{22}}}&{\frac {1}{Z_{22}}}\end{bmatrix}}$	${\begin{bmatrix}{\frac {1}{Y_{11}}}&-{\frac {Y_{12}}{Y_{11}}}\\{\frac {Y_{21}}{Y_{11}}}&{\frac {\Delta Y}{Y_{11}}}\end{bmatrix}}$	${\begin{bmatrix}H_{11}&H_{12}\\H_{21}&H_{22}\end{bmatrix}}$

Paramètres S

Article détaillé : Paramètres S.

Les paramètres S (pour scattering, diffusion) sont écrits dans une approche différente. Ici on considère, comme illustré, le quadripôle placé entre deux lignes de transmission d'impédance caractéristique $Z_{0}$ . Les paramètres S ne relient pas directement les courants et tensions mesurées au niveau des ports. Ils sont écrits en termes d'ondes incidente et réfléchie, ils dépendent non seulement des caractéristiques du quadripôle, mais aussi de la ligne de transmission^[5].

${b_{1} \choose b_{2}}={\begin{pmatrix}S_{11}&S_{12}\\S_{21}&S_{22}\end{pmatrix}}{a_{1} \choose a_{2}}$

La tension et le courant vus sur chaque ports se décomposent en fonction des ondes incidentes et réfléchies, ce qui permet de relier les paramètres S aux paramètres habituels de quadripôle. À titre d'exemple, voici leur écriture à partir des paramètres ABCD^[6] :

$S_{11}={\frac {AZ_{02}+B-CZ_{01}Z_{02}^{*}-DZ_{01}^{*}}{\alpha }}$ , $S_{12}={\frac {2(AD-BC){\sqrt {\Re (Z_{01})\Re (Z_{02})}}}{\alpha }}$ , $S_{21}={\frac {2{\sqrt {\Re (Z_{01})\Re (Z_{02})}}}{\alpha }}$ , $S_{22}={\frac {AZ_{02}^{*}+B-CZ_{01}^{*}Z_{02}-DZ_{01}}{\alpha }}$ , avec $\alpha =AZ_{02}+B+CZ_{01}Z_{02}+DZ_{01}$

Cette écriture est générique : elle prévoit que les impédances de lignes puissent être différentes à gauche et à droite ( $Z_{01}$ et $Z_{02}$ respectivement) et sont complexes. En pratique, on rencontre beaucoup de situation où les deux impédances de lignes sont égales et réelles, ce qui simplifie considérablement l'écriture.

$S_{11}={\frac {AZ_{0}+B-CZ_{0}^{2}-DZ_{0}}{\alpha }}$ , $S_{12}={\frac {2(AD-BC)Z_{0}}{\alpha }}$ , $S_{21}={\frac {2{Z_{0}}}{\alpha }}$ , $S_{22}={\frac {AZ_{0}+B-CZ_{0}^{2}-DZ_{0}}{\alpha }}$ , avec $\alpha =AZ_{0}+B+CZ_{0}^{2}+DZ_{0}$

Les paramètres-S sont particulièrement intéressants pour la caractérisation expérimentale des circuits en haute fréquence : ils sont directement mesurables à l'aide d'un analyseur de réseau^[5].

Quadripôles passifs

Quadripôles passifs élémentaires

	Résistance en série	Admittance en parallèle	Ligne de transmission	Transformateur idéal
Schéma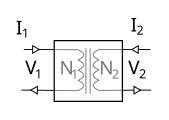
Détails	Résistance, ou plus généralement impédance en série. Remplacer R par $jL\omega$ pour une inductance, ${\frac {1}{jC\omega }}$ pour une capacité.	Admittance en parallèle. Remplacer Y par ${\frac {1}{jL\omega }}$ pour une inductance, $jC\omega$ pour une capacité.	Ligne de transmission, de type coaxial ou torsadé par exemple. $Z_{0}$ est l'Impédance caractéristique, $\gamma$ la constante de propagation, $l$ la longueur de la ligne.	Transformateur idéal $m={\frac {N_{2}}{N_{1}}}$ rapport des nombres de spires
Paramétrage transfert ${\begin{pmatrix}A&B\\C&D\end{pmatrix}}=$	${\begin{pmatrix}1&R\\0&1\end{pmatrix}}$	${\begin{pmatrix}1&0\\Y&1\end{pmatrix}}$	${\begin{pmatrix}\cosh \left(\gamma l\right)&Z_{0}\sinh \left(\gamma l\right)\\{\frac {\sinh \left(\gamma l\right)}{Z_{0}}}&\cosh \left(\gamma l\right)\end{pmatrix}}$	${\begin{pmatrix}m&0\\0&{\frac {1}{m}}\end{pmatrix}}$
Paramétrage transfert inverse ${\begin{pmatrix}A'&B'\\C'&D'\end{pmatrix}}=$	${\begin{pmatrix}1&-R\\0&1\end{pmatrix}}$	${\begin{pmatrix}1&0\\-Y&1\end{pmatrix}}$	${\begin{pmatrix}\cosh \left(\gamma l\right)&-Z_{0}\sinh \left(\gamma l\right)\\-{\frac {1}{Z_{0}}}\sinh \left(\gamma l\right)&\cosh \left(\gamma l\right)\end{pmatrix}}$	${\begin{pmatrix}{\frac {1}{m}}&0\\0&m\end{pmatrix}}$

Atténuateurs passifs

Ces atténuateurs sont des combinaisons de résistances en série et en parallèle, on retrouve donc aisément leur description matricielle à partir des formules précédentes. On note $Z_{0}$ l'impédance pour laquelle l'atténuateur est adapté, et $K$ , le ratio d'atténuation désiré.

Il est défini comme $K={\frac {V_{in}}{V_{out}}}$ , donc $K>1$ . À partir de $Z_{0}$ et $K$ , des formules permettent de déterminer les valeurs des résistances^[7].

	Atténuateur en L	Atténuateur en L, inversé	Atténuateur en π	Atténuateur en T
Schéma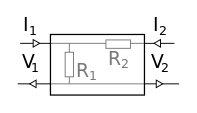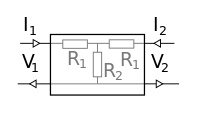
Calcul des résistances	$R_{1}=Z_{0}{\frac {K-1}{K}}$ $R_{2}={\frac {Z_{0}}{K-1}}$	$R_{1}=Z_{0}{\frac {K}{K-1}}$ $R_{2}=Z_{0}(K-1)$	$R_{1}=Z_{0}{\frac {K^{2}-1}{2K}}$ $R_{2}=Z_{0}{\frac {K+1}{K-1}}$	$R_{1}=Z_{0}{\frac {K-1}{K+1}}$ $R_{2}=Z_{0}{\frac {2K}{K^{2}-1}}$
Paramétrage transfert ${\begin{pmatrix}A&B\\C&D\end{pmatrix}}=$	${\begin{pmatrix}1&R_{1}\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\R_{2}^{-1}&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {R_{1}}{R_{2}}}&R_{1}\\R_{2}^{-1}&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {(K-1)^{2}}{K}}&Z_{0}{\frac {K-1}{K}}\\{\frac {K-1}{Z_{0}}}&1\end{pmatrix}}$	${\begin{pmatrix}1&0\\R_{1}^{-1}&1\end{pmatrix}}{\begin{pmatrix}1&R_{2}\\0&1\end{pmatrix}}$ $={\begin{pmatrix}1&R_{2}\\R_{1}^{-1}&1+{\frac {R_{2}}{R_{1}}}\end{pmatrix}}$ $={\begin{pmatrix}1&Z_{0}(K-1)\\{\frac {K-1}{Z_{0}K}}&1+{\frac {(K-1)^{2}}{K}}\end{pmatrix}}$	${\begin{pmatrix}1&0\\R_{2}^{-1}&1\end{pmatrix}}{\begin{pmatrix}1&R_{1}\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\R_{2}^{-1}&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {R_{1}}{R_{2}}}&R_{1}\\2R_{2}^{-1}+{\frac {R_{1}}{R_{2}^{2}}}&1+{\frac {R_{1}}{R_{2}}}\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {(K-1)^{2}}{2K}}&Z_{0}{\frac {K^{2}-1}{2K}}\\{\frac {K^{2}-1}{2Z_{0}K}}&1+{\frac {(K-1)^{2}}{2K}}\end{pmatrix}}$	${\begin{pmatrix}1&R_{1}\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\R_{2}^{-1}&1\end{pmatrix}}{\begin{pmatrix}1&R_{1}\\0&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {R_{1}}{R_{2}}}&2R_{1}+{\frac {R_{1}^{2}}{R_{2}}}\\R_{2}^{-1}&1+{\frac {R_{1}}{R_{2}}}\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {(K-1)^{2}}{2K}}&{\frac {Z(K^{2}-1)}{2K}}\\{\frac {K^{2}-1}{2Z_{0}K}}&1+{\frac {(K-1)^{2}}{2K}}\end{pmatrix}}$
Paramétrage transfert inverse ${\begin{pmatrix}A'&B'\\C'&D'\end{pmatrix}}=$	${\begin{pmatrix}1&0\\-R_{2}^{-1}&1\end{pmatrix}}{\begin{pmatrix}1&-R_{1}\\0&1\end{pmatrix}}$ $={\begin{pmatrix}1&-R_{1}\\-R_{2}^{-1}&1+{\frac {R_{1}}{R_{2}}}\end{pmatrix}}$ $={\begin{pmatrix}1&-Z_{0}{\frac {K-1}{K}}\\-{\frac {K-1}{Z_{0}}}&1+{\frac {(K-1)^{2}}{K}}\end{pmatrix}}$	${\begin{pmatrix}1&-R_{2}\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\-R_{1}^{-1}&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {R_{2}}{R_{1}}}&-R_{2}\\-R_{1}^{-1}&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {(K-1)^{2}}{K}}&-Z_{0}(K-1)\\-{\frac {K-1}{Z_{0}K}}&1\end{pmatrix}}$	${\begin{pmatrix}1&0\\-R_{2}^{-1}&1\end{pmatrix}}{\begin{pmatrix}1&-R_{1}\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\-R_{2}^{-1}&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {R_{1}}{R_{2}}}&-R_{1}\\-2R_{2}^{-1}-{\frac {R_{1}}{R_{2}^{2}}}&1+{\frac {R_{1}}{R_{2}}}\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {(K-1)^{2}}{2K}}&-Z_{0}{\frac {K^{2}-1}{2K}}\\-{\frac {K^{2}-1}{2Z_{0}K}}&1+{\frac {(K-1)^{2}}{2K}}\end{pmatrix}}$	${\begin{pmatrix}1&-R_{1}\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\-R_{2}^{-1}&1\end{pmatrix}}{\begin{pmatrix}1&-R_{1}\\0&1\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {R_{1}}{R_{2}}}&-2R_{1}+-{\frac {R_{1}^{2}}{R_{2}}}\\-R_{2}^{-1}&1+{\frac {R_{1}}{R_{2}}}\end{pmatrix}}$ $={\begin{pmatrix}1+{\frac {(K-1)^{2}}{2K}}&-Z_{0}{\frac {(K^{2}-1)}{2K}}\\-{\frac {K^{2}-1}{2Z_{0}K}}&1+{\frac {(K-1)^{2}}{2K}}\end{pmatrix}}$
Paramétrage S ${\begin{pmatrix}S_{11}&S_{12}\\S_{21}&S_{22}\end{pmatrix}}=$ pour $Z_{01}=Z_{02}=Z_{0}$	${\begin{pmatrix}0&{\frac {1}{K}}\\{\frac {1}{K}}&0\end{pmatrix}}$	${\begin{pmatrix}0&{\frac {1}{K}}\\{\frac {1}{K}}&0\end{pmatrix}}$	${\begin{pmatrix}0&{\frac {1}{K}}\\{\frac {1}{K}}&0\end{pmatrix}}$	${\begin{pmatrix}0&{\frac {1}{K}}\\{\frac {1}{K}}&0\end{pmatrix}}$

On remarque que les atténuateurs ont tous la même matrice S : ils sont donc équivalents. Les termes $s_{11}$ et $s_{22}$ sont nuls, ce qui exprime l'absence d'onde réfléchie.

Théorème de réciprocité dans les quadripôles passifs

Article détaillé : Théorème de réciprocité (électricité).

Les assemblage de composants passifs de base (résistance, inductance, capacités) respectent le théorème de réciprocité, illustré ci-dessus. Il existe cependant des composants passifs et linéaires qui, faisant appel à des matériaux ferromagnétiques, sont non-réciproque, et utiles grâce à cette particularité : les circulateurs et isolateurs^[8].

Lorsqu'un quadripôle est réciproque, cette propriété se retrouve dans les matrices qui le paramètrent :

Les matrices admittance et impédance sont symétriques : Y₁₂ = Y₂₁, Z₁₂ = Z₂₁,
Sur la matrice Hybride : H₁₂ = -H₂₁
Le déterminant de la matrice de transfert est égal à 1 : et ΔT = AD-BC = 1.

Quadripôle symétrique

Si les deux accès d'un quadripôle symétrique sont indiscernables: les indices correspondant, 1 et 2, des paramètres de matrices impédance ou admittance sont donc permutables sans changement. En conséquence, pour les quadripôles symétriques, en plus de posséder les propriétés de réciprocité, on a les relations Y₁₁ = Y₂₂ et Z₁₁ = Z₂₂.

Quadripôles actifs

On qualifie d'actif un circuit a la capacité de fournir de l'énergie supplémentaire.

Transistor bipolaire

L'approximation petit signal d'un transistor bipolaire est communément modélisé par le circuit équivalent en pi ci-dessus. Ce circuit est un quadripôle actif dont le paramétrage est le suivant. Il faut bien noter qu'ici les grandeurs étudiées ne sont pas les courants et tensions totaux, physiquement présents aux bornes du transistors, mais seulement leur variation autour d'un point de polarisation. Dans un modèle légèrement simpliqué où $r_{bb}$ et $r_{b'c}$ sont omis (respectivement nul et infini), le quadripôle actif est représenté par le paramétrage hydride suivant^[9], en utilisant les mêmes notations que dans le schéma:

${V_{B} \choose I_{C}}={\frac {1}{G_{\pi }+j\omega (C_{\pi }+C_{\mu })}}{\begin{pmatrix}1&j\omega C_{\mu }\\g_{m}-j\omega C_{\mu }&q(j\omega )\end{pmatrix}}{I_{B} \choose V_{C}}$ Avec : $q(j\omega )=G_{\pi }+j\omega (C_{\pi })(G_{0}+j\omega (C_{\mu }))+j\omega (C_{\mu })(G_{\pi }+g_{m})$

Transistor a effet de champs

De façon similaire, un transistor MOSFET utilisé en petit signal autour d'un point de polarisation se modélise par le circuit en pi ci-dessus. Ici, le paramétrage en Z est le plus commode^[9] :

${V_{GS} \choose V_{DS}}={\begin{pmatrix}{\frac {1}{j\omega (C_{g}s)}}&0\\{\frac {-g_{m}r_{0}}{j\omega (C_{g}s)}}&-r_{0}\end{pmatrix}}{I_{G} \choose I_{D}}$

Amplificateur

Dans l'exemple d'un amplicateur inverseur de tension, la matrice ABCD s'écrit ainsi (les courants étant notés positivement vers l'intérieur du montage) ^[10] :

${V_{e} \choose I_{e}}={\begin{pmatrix}-{\frac {R_{1}}{R_{2}}}&0\\-{\frac {1}{R_{2}}}&0\end{pmatrix}}{V_{s} \choose -I_{s}}$ ,

Le déterminant de cette matrice est nul : en effet un tel montage ne respecte pas le théorème de réciprocité. Physiquement, les deux zéros à droite signifient que le courant $I_{s}$ peut changer sans influencer les valeurs en entrée.

Opérations sur les quadripôles

Impédances d'entrée et de sortie

On représente ici un quadripôle intercalé entre un générateur de Thévenin et une impédance de charge. On peut alors s'intéresser :

A l'impédance « vue » par le générateur, et représentant le quadripôle plus sa charge.
Au générateur équivalent « vue » par la charge $Z_{L}$ et représentant la générateur et le quadripôle.

Pour le premier problème, en chargeant le quadripôle avec la charge $Z_{L}$ , on impose : $V_{2}=-Z_{L}I_{2}$ (le signe moins étant dû aux conventions de sens des courants). Cette contrainte supprime un degré de liberté du système.

En reprenant le paramétrage en impédance du quadripôle : ${V_{1} \choose V_{2}}={\begin{pmatrix}Z_{11}&Z_{12}\\Z_{21}&Z_{22}\end{pmatrix}}{I_{1} \choose I_{2}}$ devient : ${V_{1} \choose -Z_{L}I_{2}}={\begin{pmatrix}Z_{11}&Z_{12}\\Z_{21}&Z_{22}\end{pmatrix}}{I_{1} \choose I_{2}}$

La seconde ligne permet d'exprimer $I_{2}$ en fonction de $I_{1}$ , et en remplaçant dans la première, on obtient la relation entre $V_{1}$ et $I_{1}$ , soit l'impédance de charge formée par le quadripole et $Z_{L}$ .

$V_{1}=Z_{11}I_{1}-{\frac {Z_{12}Z_{21}}{Z_{L}+Z_{22}}}I_{1}$ $V_{1}=\left(Z_{11}-{\frac {Z_{12}Z_{21}}{Z_{L}+Z_{22}}}\right)I_{1}=Z_{\mathrm {in} }I_{1}$

Fonction de transfert

En reprenant le schéma ci-dessus et ses notations, on s'intéresse à la fonction de transfert, connaissance les paramètres ABCD du quadripôle :

$F_{t}={\frac {V_{2}}{V_{0}}}={\frac {Z_{L}}{AZ_{L}+B+CZ_{L}Z_{S}+DZ_{S}}}$

Association de deux quadripôles

Deux quadripôles peuvent être associés (pour en former un nouveau) de cinq façons différentes. Dans chaque cas, l'un des paramétrage est bien adapté, car il permet d'obtenir la matrice du nouveau quadripôle obtenu par une opération simple à partir des matrices représentant les deux quadripôles de départ.

Désignation	Schéma	Propriétés
Série		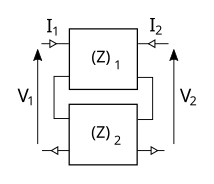${Z}={Z_{1}}+{Z_{2}}$ Les matrices impédance s'ajoutent.
Parallèle		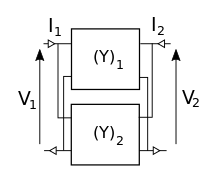${Y}={Y_{1}}+{Y_{2}}$ Les matrices admittance s'ajoutent.
Parallèle-série		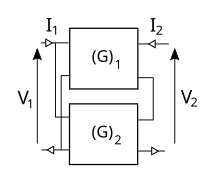${G}={G_{1}}+{G_{2}}$ Les matrices hybrides inverses s'ajoutent.
Série-parallèle		${H}={H_{1}}+{H_{2}}$ Les matrices hybrides s'ajoutent.
Cascade		${T}={T_{1}}\times {T_{2}}$ ${T'}={T'_{2}}\times {T'_{1}}$ Les matrices de transfert se multiplient. Le sens de la multiplication est différent pour T et T' : le produit matriciel est généralement non commutatif.

Caractérisation expérimentale

Ancien analyseur de réseau Hewlett-Packard 8720A

L'analyseur de réseau est un instrument dédié spécifiquement à la mesure des paramètres S d'un quadripôle. L'instrument dispose de deux sorties coaxiales qui lui permettent de mesurer les termes de la matrice S.

Hors de l'électronique

L'analogie électro-mécanique permet d'utiliser le formalisme des quadripôles pour des systèmes mécaniques ou électro-mécaniques. Dans ce cas, les deux ports, ou un seul, présentent, en remplacement des grandeurs électrique courant et tension, un couple de grandeur mécanique (force et vitesse, pression et vitesse, couple et vitesse angulaire selon le système étudié).

Ainsi l'étude des transducteurs piézoélectriques, dans une approximation unidimensionnelle, fait appel à des circuits équivalents formés de quadripôles. Les deux circuits les plus communs sont ceux de Mason et de KLM. Dans chacun de ces circuits, l'effet piézoélectrique est représenté par un quadripôle dont l'entrée est électrique, et dont la sortie est la vitesse et la pression (ou la force) au centre de la couche piézoélectrique, tandis que chaque couche est un quadripôle mécanique, correspondant à une ligne de transmission^[11].

Notes et références

↑ Commission électrotechnique internationale, ISO 60050 Vocabulaire électrotechnique international, 1987/2019 (lire en ligne), p. 131-12-66 Théorie du circuit : quadripôle.
↑ Tahar Neffati, L'électronique de A à Z, Paris, Dunod, 2006, p. 240-245 « quadripôle ».
↑ Richard C. Dorf et James A. Svoboda, Introduction to Electric Circuits, John Wiley & Sons, 7 janvier 2010, 886 p. (ISBN 978-0-470-52157-1, lire en ligne)
↑ (en) G. G. Johnstone et J. H. B. Deane, « Relations between two-port parameters », International Journal of Electronics, vol. 71, n^o 1,‎ juillet 1991, p. 107–116 (ISSN 0020-7217 et 1362-3060, DOI 10.1080/00207219108925462, lire en ligne, consulté le 19 mars 2019)
↑ ^{a et b} S. Sercu et L. Martens, « Characterizing N-port packages and interconnections with a 2-port network analyzer », Electrical Performance of Electronic Packaging, IEEE,‎ 1997, p. 163–166 (ISBN 9780780342033, DOI 10.1109/EPEP.1997.634062, lire en ligne, consulté le 22 mars 2019)
↑ D.A. Frickey, « Conversions between S, Z, Y, H, ABCD, and T parameters which are valid for complex source and load impedances », IEEE Transactions on Microwave Theory and Techniques, vol. 42, n^o 2,‎ février 1994, p. 205–211 (DOI 10.1109/22.275248, lire en ligne, consulté le 22 mars 2019)
↑ All About Circuits, Textbook
↑ (en) Negar Reiskarimian et Harish Krishnaswamy, « Magnetic-free non-reciprocity based on staggered commutation », Nature Communications, vol. 7, n^o 1,‎ décembre 2016 (ISSN 2041-1723, PMID 27079524, PMCID PMC4835534, DOI 10.1038/ncomms11217, lire en ligne, consulté le 24 mars 2019)
↑ ^{a et b} EECS 142 Two-Port Networks and Amplifiers A. M. Niknejad (Cours de Berkeley)
↑ ECE 580 – Network Theory, Oregon State University
↑ (en) S. Sherrit, S.P. Leary, B.P. Dolgin et Y. Bar-Cohen, « Comparison of the Mason and KLM equivalent circuits for piezoelectric resonators in the thickness mode », 1999 IEEE Ultrasonics Symposium. Proceedings. International Symposium, vol. 2,‎ 1999, p. 921–926 (DOI 10.1109/ULTSYM.1999.849139).

Voir aussi

Portail de l’électricité et de l’électronique