Point de Lagrange

Pour les articles homonymes, voir point et Lagrange.

« Point de libration » et « Point d'Euler » redirigent ici. Pour les autres significations, voir Libration et Euler (homonymie).

Un point de Lagrange (noté L1 à L5), ou, plus rarement, point de libration, est une position de l'espace où les champs de gravité de deux corps en mouvement orbital l'un autour de l'autre, et de masses substantielles, fournissent exactement la force centripète requise pour que ce point de l'espace accompagne simultanément le mouvement orbital des deux corps. Dans le cas où les deux corps sont en orbite circulaire, ces points représentent les endroits où un troisième corps, de masse négligeable, resterait immobile par rapport aux deux autres, au sens où il accompagnerait à la même vitesse angulaire leur rotation autour de leur centre de gravité commun sans que sa position par rapport à eux n'évolue.
Au nombre de cinq, ces points se scindent en deux points stables dénommés L4 et L5, et en trois points instables notés L1, L2 et L3. Ils sont nommés en l'honneur du mathématicien français Joseph-Louis Lagrange[1]. Ils interviennent dans l'étude de certaines configurations d'objets du Système solaire (principalement pour les points stables) et dans le placement de divers satellites artificiels (principalement pour les points instables). Ce sont les points remarquables de la « géométrie de Roche[2] » (points-col et extrema), laquelle permet notamment de classer les différents types d'étoiles binaires.
Les trois points L1, L2 et L3 sont parfois appelés les points d'Euler, en l'honneur de Leonhard Euler, l'appellation de points de Lagrange étant alors réservée aux deux points L4 et L5[3].
Les points L4 et L5, en raison de leur stabilité, peuvent naturellement attirer ou retenir longtemps des objets et sont donc peu utilisables à cause du risque de collision, alors qu'au contraire, les points L1, L2 et L3, étant instables, ne peuvent pas maintenir naturellement des objets, mais peuvent être utilisés par des missions spatiales moyennant des corrections d’orbite peu coûteuses en termes de carburant.
Historique
En mécanique céleste, il est un sujet qui a passionné de nombreux mathématiciens : c'est le problème dit des trois corps. Newton, après avoir énoncé sa loi qui exprime que « les corps s'attirent avec une force proportionnelle au produit de leur masse et inversement proportionnelle au carré de la distance de leurs centres », a cherché à décrire le comportement de trois corps sans y parvenir. Il faut attendre le mathématicien Joseph-Louis Lagrange qui, en 1772, étudia le cas d'un petit corps, de masse négligeable (ce qu'on appelle aujourd'hui corps d'épreuve ou particule-test), soumis à l'attraction de deux plus gros : le Soleil et, par exemple, une planète. Il découvrit qu'il existait des positions d'équilibre pour le petit corps, des endroits où toutes les forces se compensent.
Définition
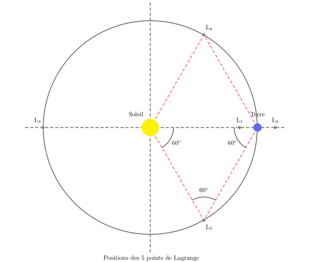
Un objet de faible masse situé en ces points ne bouge plus relativement aux deux autres corps, et tourne de concert avec eux (par exemple une planète et le Soleil). Si on donne en exemple les points de Lagrange du système Soleil-Terre, ces cinq points sont notés et définis comme suit (échelle non respectée) :
- L1 : sur la ligne définie par les deux masses, entre celles-ci, la position exacte dépendant du rapport de masse entre les deux corps ; dans le cas où l'un des deux corps a une masse beaucoup plus faible que l'autre, le point L1 est situé nettement plus près du corps peu massif que du corps massif ;
- L2 : sur la ligne définie par les deux masses, au-delà de la plus petite. Dans le cas où l'un des deux corps a une masse beaucoup plus faible, la distance de L2 à ce corps est comparable à celle entre L1 et ce corps ;
- L3 : sur la ligne définie par les deux masses, au-delà de la plus grande. Dans le cas où l'un des deux corps est notablement moins massif que l'autre, la distance entre L3 et le corps massif est comparable avec celle entre les deux corps ;
- L4 et L5 : sur les sommets des deux triangles équilatéraux dont la base est formée par les deux masses. L4 est celui des deux points en avance sur l'orbite de la plus petite des masses, dans son orbite autour de la grande, et L5 est en retard[4]. Ces points sont parfois appelés points de Lagrange triangulaires ou points troyens, du fait que c'est le lieu où se trouvent les astéroïdes troyens du système Soleil-Jupiter. Contrairement aux trois premiers points, ces deux derniers ne dépendent pas des masses relatives des deux autres corps.
Calcul de la position des points de Lagrange
Le calcul de la position des points de Lagrange se fait en considérant l'équilibre d'un corps de masse négligeable entre le potentiel gravitationnel créé par deux corps en orbite et la force centrifuge. La position des points L4 et L5 peut être obtenue analytiquement. Celle des trois autres points L1 à L3 s'obtient en résolvant numériquement, ou éventuellement à l'aide d'un développement limité, une équation algébrique. La position de ces trois points est donnée dans le tableau ci-dessous, dans le cas où la masse d'un des deux corps (en l'occurrence le numéro 2) est négligeable devant l'autre, situé à une distance R du précédent. Les positions sont données le long de l'axe reliant les deux corps, dont l'origine est identifiée au centre de gravité du système, et dont l'orientation va du corps 1 au corps 2. Les quantités r2 = (1-q)R et q dénotent respectivement la position du corps 2 sur l'axe et le rapport de la masse du corps le plus léger à la masse totale des deux corps. Enfin, on utilise la quantité ε définie par ε = (q / 3)1/3.
| Point | Position par rapport au centre de gravité du système |
|---|---|
| L1 | |
| L2 | |
| L3 |
Dans la littérature, on trouve parfois des expressions quelque peu différentes, du fait que l'origine de l'axe est prise ailleurs que sur le centre de gravité, et que l'on utilise comme terme à la base du développement limité le rapport entre les deux masses plutôt que le rapport de la plus petite à la masse totale, c'est-à-dire que l'on utilise parfois la quantité q' définie par .
- Préliminaires
On note M1 et m2 la masse des deux corps, la masse du premier étant supposée supérieure ou égale à celle du second. Les deux corps sont supposés être en orbite circulaire, leur séparation étant R. Les deux corps orbitent autour de leur centre de gravité commun. On note r1 et r2 les distances algébriques des deux corps par rapport au centre de gravité commun selon un axe orienté du corps 1 au corps 2 (c'est-à-dire que r1 va être négatif et r2 positif). Le centre de gravité est défini par l'équation
- ,
avec par définition de la distance R,
- .
Ces deux équations ont pour solution
- ,
- ,
où on a noté M = M1 + m2 la masse totale du système.
Les deux corps orbitent l'un autour de l'autre à une vitesse angulaire ω, dont la valeur est donnée par la troisième loi de Kepler :
- ,
G étant la constante de gravitation.
Si l'on se place dans le référentiel tournant avec les deux corps, c'est-à-dire à la vitesse angulaire ω, un corps immobile sera soumis, outre aux forces gravitationnelles des deux corps, à la force centrifuge. Si on note r le rayon vecteur de ce corps, la force centrifuge par unité de masse fc à laquelle il sera soumis s'écrit
- .
- Équation fondamentale
La définition d'un point de Lagrange est que la somme des forces gravitationnelles et inertielles s'annule en ces points. En notant r le rayon vecteur du ou des points en question, on a ainsi
- ,
les doubles barres indiquant que l'on prend la norme des vecteurs considérés. On remplace ensuite la vitesse angulaire ω par sa valeur issue de la troisième loi de Kepler, ce qui donne
- ,
que l'on simplifie immédiatement par la constante de gravitation
- .
C'est la résolution de cette équation qui donne les différents points de Lagrange.
- Les deux cas à considérer
La projection de cette équation perpendiculairement au plan de l'orbite, dont la normale est donnée par un vecteur noté donne immédiatement
- ,
ce qui implique que l'ensemble des points de Lagrange est situé dans le plan de l'orbite. La résolution de l'équation se fait donc dans le plan orbital. Deux cas sont à considérer :
- celui où l'on cherche un point le long de l'axe formé par les deux corps,
- celui où l'on cherche un point en dehors de cet axe.
- Cas des points L4 et L5
On suppose que le rayon vecteur r n'est pas parallèle à l'axe passant par les deux corps. On projette donc l'équation fondamentale perpendiculairement à cet axe, direction que l'on suppose définie par un vecteur noté . Par définition, cette direction étant perpendiculaire à l'axe reliant les deux corps, on a
- .
L'équation fondamentale se réécrit donc
- .
Les termes en se simplifient, ce qui donne
- .
On définit maintenant la direction comme la perpendiculaire à r. Comme r n'est pas colinéaire à r1 et r2, les quantités ne sont pas nulles. En projetant l'équation fondamentale le long de s, on obtient
- .
Or, d'après le théorème de Thalès, les projections de r1 et r2 le long de sont dans le même rapport que les projections de ces vecteurs le long de l'axe reliant les deux corps. Il s'ensuit que l'équation précédente peut se réécrire
- .
Le barycentre des deux corps implique, comme vu précédemment, que
- .
La combinaison de cette équation et celle qui précède implique donc que les deux distances et sont identiques, leur valeur étant notée R' :
- .
En injectant ce résultat sur la projection le long de r, il vient alors
- .
En multipliant le tout par R'3 et en se souvenant que M est la somme des deux masses, on obtient finalement
- ,
ce qui donne finalement
- ,
c'est-à-dire que les points cherchés forment un triangle équilatéral avec les deux corps du système. Ces triangles sont de plus inclus dans le plan orbital, ce qui donne deux points possibles, notés comme annoncé L4 et L5, étant situé de part et d'autre de l'axe reliant les deux corps.
En utilisant le théorème de Pythagore, la distance D de ces deux points de Lagrange du centre de gravité du système s'écrit
- ,
ce qui donne
- ,
ce qui donne
- .
En utilisant le fait que , il vient
- .
- Cas des points L1 à L3
Dans le cas où l'on considère des points de Lagrange situés sur l'axe reliant les deux corps, trois sous-cas sont à considérer :
- Le cas où le ou les points sont entre les corps 1 et 2 ;
- Le cas où le ou les points sont à l'opposé du corps 2 par rapport au corps 1 ;
- Le cas où le ou les points sont à l'opposé du corps 1 par rapport au corps 2.
Dans ces trois cas, l'équation fondamentale se réécrit de la façon suivante :
- Cas 1 : la projection des deux forces sur l'axe a des signes opposés (la projection de la force exercée par le corps 1 est négative, celle de la force exercée par le corps 2 est positive), ce qui donne
- ,
- avec
- .
- Cas 2 : la projection des deux forces sur l'axe est négative, ce qui donne
- ,
- avec
- .
- Cas 3 : la projection des deux forces sur l'axe est positive, ce qui donne
- ,
- avec
- .
Chacune de ces trois équations peut se ramener à une équation polynomiale du cinquième degré, pour laquelle il n'existe pas de solution analytique exacte, sauf cas particulier (comme celui des deux masses identiques, par exemple).
L'unicité des solutions dans chacun des trois cas se déduit du fait que l'équation à résoudre sur l'équilibre des forces dérive d'un potentiel U, donné par
- .
- Forme réduite et solution dans le cas où le rapport entre les masses est faible
Quand le rapport entre m2 et M1 (ou entre m2 et M) est faible, on peut trouver une solution approchée pour la position de chacun des points en effectuant un développement limité à partir d'une solution approchée facile à trouver. Pour simplifier les notations, on effectue un changement d'échelle afin d'exprimer toutes les longueurs en unité de la séparation R et les masse en unité de la masse totale M. On pose ainsi
- ,
et
- ,
et on définit le petit paramètre q par
- ,
à partir de quoi on peut exprimer
- ,
- ,
- .
Dans ce cas là, les trois équations écrites ci-dessus prennent la forme plus simple
- Cas 1 :
- ,
- avec
- .
- Cas 2 : la projection des deux forces sur l'axe est négative, ce qui donne
- ,
- avec
- .
- Cas 3 : la projection des deux forces sur l'axe est positive, ce qui donne
- ,
- avec
- .
- Le point L1
Quand la masse du corps 2 est négligeable, l'attraction de celui-ci est négligeable sauf si la particule d'épreuve est très proche. Or, quand l'attraction du corps 2 est négligeable, l'équilibre entre l'attraction du corps 1 et la force centrifuge est tel que la distance du point d'équilibre est de l'ordre de R. Quand le point d'équilibre est situé à l'opposé du corps 2, on est dans le cas du point de Lagrange L3, qui est donc, en gros, situé à l'opposé du corps 2 par rapport au corps 1. Dans le cas contraire, on va donc supposer que le point d'équilibre est plutôt proche du corps 2 (et donc à nouveau situé à la distance R du corps 1), mais néanmoins suffisamment éloigné pour que l'attraction du corps 2 exercée sur la particule d'épreuve reste petite par rapport à celle du corps 1. On pose donc à partir de la forme réduite
- ,
où ici ε' est une quantité petite et négative (on suppose ici que le point est entre les deux corps). L'équation réduite se transforme alors en
- .
On effectue un développement limité au premier ordre de l'attraction produite par le corps 1 :
- .
Les termes en 1 - q se simplifient, et il reste
- .
Toujours en ne gardant que les termes d'ordre le plus bas en q, il vient
- .
On peut par la suite continuer le calcul, en développant l'écart du point au corps 2 en puissances de ε'. On pose ainsi
- .
L'équation fondamentale réduite donne alors
- .
On peut factoriser le second terme avec q / ε'2, que l'on peut remplacer par sa valeur, soit -3 ε'. On obtient alors
- .
On effectue ensuite un développement limité des deux premiers termes, au second ordre pour le premier et au premier ordre pour le suivant, ce qui donne
- ,
d'où on déduit que x vaut un tiers, ce qui donne
- .
Le développement peut ensuite être continué suivant la même procédure. À l'ordre suivant, on a ainsi
- .
- Le point L2
Le cas du point L2 se résout exactement comme dans la section précédente, si ce n'est que le signe du second terme de l'équation fondamentale est négatif. On pose donc
- ,
ε étant cette fois-ci supposé petit et positif, et on a ainsi
- .
La résolution à l'ordre le plus bas donne
- ,
qui après annulation des termes donne
- ,
soit
- .
Cela correspond au signe près au même résultat que précédemment. La suite du développement de la solution se fait de même que précédemment. On part de
- ,
et on injecte ce résultat dans l'équation fondamentale
- .
Comme précédemment, on transforme cette expression selon
- ,
ce que l'on résout en
- ,
soit
- .
Cette expression est identique à celle du premier point de Lagrange en remplaçant ε' par ε, mais ces deux points sont dissymétriques : comme le signe de ε, ε' change entre le point L1 et le point L2, la correction du second ordre, toujours positive, rapproche le point L1 du corps 2 alors qu'elle éloigne le point L2 : les deux points ne sont plus à égale distance du corps 2. Pour la Terre, le rapport de masse est de 1⁄300 000, et ε est de l'ordre 0,01, ce qui place les deux points par rapport à la Terre à une distance d'environ un centième de la distance Terre-Soleil, soit dans les 1 500 000 kilomètres. Le terme de second ordre est de l'ordre d'un trente-millième de la distance Terre-Soleil, soit dans les 5 000 km. Le point L1 est donc environ 10 000 km plus près de la Terre que ne l'est L2.
Enfin, on peut poursuivre le développement à l'ordre supérieur, ce qui donne, tous calculs faits
- .
- Le point L3
Dans le cas 3, qui va correspondre au point L3, l'équation fondamentale s'écrit
- .
Comme le point est supposé au-delà du corps 1 par rapport au corps 2, il est plus proche du corps le plus massif, dont l'attraction va être prépondérante par rapport à l'autre corps. Dans la situation où l'on se place, le point recherché a donc sa position approximée par
- .
La solution approchée de cette équation est, bien sûr
- .
Pour trouver les écarts à cette valeur, on écrit dans l'équation fondamentale
- ,
et on résout l'équation en prenant en compte les premiers termes en q. On obtient ainsi
- .
Les quantités et q étant petites devant R, le premier terme s'écrit
- .
Le second terme étant négligeable par rapport au précédent (il est proportionnel à q), il peut s'approximer en
- .
En combinant l'ensemble de ces termes, on obtient
- ,
ce qui donne
- ,
c'est-à-dire
- .
On peut sans difficulté continuer ce calcul en posant désormais
- ,
étant cette fois proportionnel à q2. L'équation fondamentale devient alors
- ,
c'est-à-dire
- .
En développant cette expression au second ordre en q, on trouve
- ,
c'est-à-dire que est au plus en q3. En refaisant le calcul dans ce cadre là, on trouve finalement
- .
Stabilité



Le calcul ci-dessus n'indique en rien si les points de Lagrange sont stables. La stabilité ou non de ces points est du reste peu intuitive. Dans le référentiel tournant avec les deux corps, une particule d'épreuve peut être vue comme soumise à un potentiel incluant la contribution gravitationnelle et celle de la force centrifuge. Ce potentiel, noté Ω, s'écrit ainsi
- .
Tous les termes de ce potentiel sont négatifs et décroissent à mesure que l'on s'éloigne des masses (pour les deux premiers termes) ou du centre de gravité du système (pour le troisième). On peut ainsi montrer que les points de Lagrange L4 et L5 sont des maxima locaux du potentiel Ω (voir ci-dessous) et que les trois autres points sont des points selles. D'ordinaire, une position d'équilibre (déterminée par l'annulation des dérivées du potentiel) est stable uniquement si on se situe dans des minima locaux du potentiel. Cependant, étant donné que l'on est dans un référentiel tournant, le référentiel est non inertiel. Un objet se déplaçant dans ce référentiel, par exemple au voisinage d'une position d'équilibre, va être soumis à la force de Coriolis, et son mouvement ne dépend pas uniquement de la forme du potentiel. Pour étudier la stabilité des points de Lagrange, il faut donc tenir compte de la force de Coriolis.
Pour calculer la stabilité des points de Lagrange, il faut ainsi étudier l'équation du mouvement d'un objet situé au voisinage d'un de ces points. En notant δR le vecteur de coordonnées δX et δY donnant l'écart d'un tel objet à un des points de Lagrange (que l'on suppose confiné au plan orbital), l'équation du mouvement s'écrit
- ,
où δf représente la force par unité de masse exercée sur l'objet. Cette force est petite du fait qu'au point de Lagrange la force (constituée d'une composante gravitationnelle et de la force centrifuge) est nulle et que l'on se place à proximité d'un tel point. Cette force peut se calculer en termes d'un développement limité. Par exemple, pour la composante X, on a
- .
Le premier terme correspond à la force s'exerçant au point de Lagrange, force qui est nulle par construction. Par ailleurs, la force dérivant d'un potentiel, on peut exprimer les dérivées de la force en termes de dérivées secondes du potentiel :
- .
On peut ainsi exprimer l'équation du mouvement en termes des composantes selon
- ,
- .
Ce groupe d'équations peut être mis sous la forme d'un système de quatre équations différentielles du premier ordre :
- ,
où les dérivées partielles du potentiel Ω ont été notées en indice précédé d'une virgule (par exemple, Ω,xx correspond à ).
La stabilité du point de Lagrange considéré est obtenue en recherchant les solutions de cette équation. Pour cela, il suffit de trouver des solutions de type exponentielle, en . On va ainsi procéder à la diagonalisation de la matrice ci-dessus, que l'on notera A. Les valeurs propres trouvées vont correspondre aux quantités Γ ci-dessus, les écarts à la position d'équilibre étant alors une certaine combinaison d'au plus quatre exponentielles. La stabilité du système est assurée par le fait que les exponentielles ne croissent pas au cours du temps, c'est-à-dire que les quantités Γ sont soit négatives, soit complexes à parties réelles négatives. En fait, il n'est pas nécessaire de diagonaliser complètement la matrice, il suffit d'en trouver les valeurs propres, c'est-à-dire les solutions de l'équation
- .
Ce déterminant s'écrit
- ,
et il vaut
- .
Cette équation peut se ramener à une équation polynomiale du second ordre en λ2. Les solutions de l'équation de départ sont donc deux couples de nombres opposés deux à deux. Pour que deux nombres opposés soient négatifs ou nuls ou alors de partie réelle négative ou nulle, il faut obligatoirement qu'ils soient des nombres imaginaires purs, donc que les solutions de l'équation en λ2 soient réelles et négatives. Pour que ces solutions soient réelles, il faut donc que le discriminant soit positif, soit ici
- .
Une fois ceci obtenu, il faut que les deux solutions réelles soient négatives, ce qui implique que simultanément leur somme soit négative et leur produit positif, ce qui implique
- ,
- .
La stabilité d'un point de Lagrange est soumise à la réalisation de ces trois contraintes. Parmi ces contraintes, la dernière a une interprétation simple : le signe de la quantité détermine si la position considérée est un extrémum local ou un point selle. En l'occurrence, la positivité de cette quantité implique qu'elle doive être un extrémum local, condition nécessaire mais non suffisante à la stabilité du point de Lagrange. Quand cette quantité est négative, on a un point selle et le point de Lagrange est instable. Par contre, de façon plus surprenante, un point de Lagrange peut être stable s'il correspond à un maximum local du potentiel, c'est-à-dire que Ω,xx + Ω,yy peut être négatif, pourvu que cette quantité ne dépasse pas la valeur critique de -4 ω2. En pratique, c'est ce qui se produit dans certains cas pour les points de Lagrange L4 et L5. L'interprétation physique de cette situation est que la stabilité est alors assurée par la force de Coriolis. Un objet légèrement décalé d'un tel point va s'en éloigner dans un premier temps en façon radiale, avant de voir sa trajectoire incurvée par la force de Coriolis. Si le potentiel est partout décroissant autour du point, alors il est possible que la force de Coriolis force l'objet à tourner autour du point de Lagrange, à l'instar des nuages dans une dépression qui ne se dirigent pas vers le cœur de la dépression, mais sont contraints à une trajectoire circulaire autour de celui-ci.
- Préliminaire
Pour étudier la stabilité des points de Lagrange, on va être amené à calculer les dérivées successives du potentiel. Ce potentiel fait intervenir la distance |r - r1|. Il faut donc connaître les dérivées des différentes puissances d'une telle quantité. En coordonnées cartésiennes, cette quantité s'écrit
- .
Sa dérivée par rapport à l'une des coordonnées x, y, z, collectivement notées xi s'écrit donc
- .
La dérivée d'une puissance p quelconque de cette grandeur est donc
- .
En adaptant ce résultat aux dérivées secondes des quantités intervenant dans le potentiel, on a
- ,
ce qui, pour le potentiel complet, donne
- ,
où δij représente le symbole de Kronecker. C'est la valeur de ces dérivées partielles qu'il faut calculer pour déterminer la stabilité des différents points de Lagrange. C'est pour les points de Lagrange L4 et L5 que ce calcul est le plus simple.
- Cas des points de Lagrange L4 et L5
Ces points se caractérisent par le fait que leur distance aux deux corps est identique et égale à R :
- .
Par ailleurs, on peut utiliser la troisième loi de Kepler pour passer des quantités du type G M / R3 à ω, et on connaît les coordonnées exactes des points de Lagrange. En évaluant les dérivées du potentiel aux points de Lagrange L4 ou L5, on a
- ,
et
- ,
le signe + s'appliquant pour L5 et le signe - pour L4. Finalement, la matrice recherchée a pour composantes
- .
Le déterminant de cette matrice vaut
- ,
qui est toujours positif puisque q est confiné entre 0 et 1. Cette première condition de stabilité est établie. La seconde condition de stabilité s'écrit
- ,
quantité là encore positive. Enfin, le discriminant donne
- .
La stabilité des deux points est, finalement, déterminée par la positivité de la quantité . Les zéros qa, qb de ce polynôme sont donnés par la formule usuelle, qui ici indique
- .
Ce polynôme a ainsi des valeurs négatives sur la plage . Ainsi, la stabilité de ces deux points de Lagrange n'est assurée que si la plus petite masse n'excède pas 3,852 % de la masse totale, ou, de façon équivalente, que le rapport des deux masses n'excède pas 4,006 %[6].
Cette condition est vérifiée pour toutes les configurations de type Soleil-Planète (où q n'excède pas environ un millième pour Jupiter), ou pour le système Terre-Lune (où q est de l'ordre de 1/80, soit 1,25 %).
- Cas des points de Lagrange L1 à L3
Les trois points de Lagrange L1 à L3 sont situés sur l'axe reliant les deux corps. Dans la formule qui donne les dérivées secondes, les quantités yi - y1 i sont nulles, alors que leurs analogues en x s'identifient aux distances entre un des corps et le point de Lagrange considéré. En conséquence, la matrice des dérivées secondes s'écrit
- .
Le terme Ω,xx est manifestement négatif. Le signe du déterminant de la matrice est déterminé par celui de Ω,yy : si ce dernier est positif, alors le point de Lagrange est un point selle et il est instable. On peut réécrire ce terme en utilisant la troisième loi de Kepler :
- .
- Le cas de L1
Le point de Lagrange L1 est situé entre les deux corps. Sa distance à ceux-ci, |r - r1| et |r - r2| est donc, à chaque fois, strictement inférieure à R. On a ainsi
- .
Cette quantité est donc strictement positive, ce qui assure que le déterminant est négatif, c'est-à-dire que L1 est un point selle, ce qui en fait un point instable.
- Le cas de L2 et L3
On pose, pour simplifier les notations,
- ,
- .
On s'intéresse donc au signe de la quantité
- ,
soit
- ,
sachant que u1 et u2 sont reliés entre eux par le fait que leur différence est égale à 1 et qu'ils définissent un point de Lagrange, soit la relation
- .
La distance du point de Lagrange au centre de gravité du système peut s'écrire, pour le point L2,
- ,
relations que l'on peut combiner en
- .
La position du point L2 est donc donnée par
- .
On pose alors
- ,
- .
On a donc, d'une part
- ,
et, d'autre part
- .
Autrement dit,
- .
Le premier terme du membre de droite est nul en vertu de la relation A + B = 0. Il reste donc
- .
Or, pour le point L2, on est situé plus près du corps 2 que du corps 1. Par conséquent, u2 est plus petit que u1, et, par conséquent, est positif. Le signe de la dérivée seconde correspond donc à celui de B, qui lui-même est déterminé par la valeur de u2 : si cette quantité est supérieure à 1, alors B est négatif, alors que, dans le cas contraire, B est positif, ce qui implique que le point est instable. Le point de Lagrange L2 est situé au-delà du corps 2. La force totale (gravitationnelle plus centrifuge) s'exerçant dans cette région est d'abord tournée vers le corps 2 quand on est proche de celui-ci, puis s'annule en L2 et est après dirigée à l'opposé de L2. Au point tel que u2 vaut 1, la composante de cette force, selon l'axe reliant les deux corps, est donnée (à une constante multiplicative positive près) par
- ,
avec, ici,
- ,
- ,
soit
- .
Temps caractéristiques en L1 et L2 pour les systèmes à grande hétérogénéité de masse
Une des applications les plus importantes de l'instabilité des points de Lagrange, L1 et L2, réside dans le fait que des satellites artificiels peuvent être envoyés en ces points du système Terre-Soleil (voir ci-dessous). Pour de tels satellites, des corrections de trajectoires régulières doivent être appliquées afin de conserver le satellite au voisinage du point. Ce temps caractéristique peut être évalué dans le cas où le rapport de masse des deux corps du système est élevé. Dans ce cas, le temps caractéristique γ-1 d'instabilité est donné par
- ,
où T est la période orbitale du système. Dans le cas du système Terre-Soleil, où T est légèrement supérieur à 365 jours, le temps caractéristique d'instabilité est alors de 23 jours et 4 heures.
Par ailleurs, la composante stable de la trajectoire se fait à la pulsation
- ,
soit, de façon équivalente, avec la période
- ,
ce qui, dans le même cas de figure que ci-dessus, donne une période de 176 jours.
L'équation donnant les valeurs propres du système est toujours
- ,
avec, pour les points L1 et L2,
- ,
- ,
- .
en se restreignant aux termes d'ordre le plus bas en q, u1 vaut 1, et u2 est déterminé par la relation donnée par le premier tableau de cette page. On a ainsi
- ,
- .
L'équation polynomiale devient alors
- ,
dont les solutions sont
- .
La solution positive à cette équation indique que les écarts au point d'équilibre croissent exponentiellement au cours du temps selon la relation
- ,
avec
- .
Le temps caractéristique associé est donc
- ,
soit, comme annoncé, un temps caractéristique de l'ordre de 23 jours pour les points de Lagrange de la Terre.
De la même façon, il existe des trajectoires périodiques dont la pulsation est donnée par les racines complexes de l'équation, soit
- ,
c'est-à-dire une période de
- ,
La structure des orbites en présence d'instabilité
Une fois les valeurs propres d'un point instable connues, une trajectoire au voisinage d'un point de Lagrange va être une combinaison linéaire des vecteurs propres associés aux valeurs propres. En notant λi l'une de ces valeurs propres, le vecteur propre associé a pour composantes
- ,
avec
- ,
et une trajectoire est de la forme
- ,
où les quantités sont des nombres quelconques déterminés par la valeur des δX, δY et de leur dérivée à un instant donné. Dans le cas des trois points de Lagrange instables, le déterminant de la matrice des dérivées secondes est négatif, ce qui implique que le discriminant de l'équation du second degré en λ2 possède des racines réelles de signes opposés, et que, au terme, les valeurs propres recherchées sont deux nombres imaginaires purs opposés et deux nombres réels opposés. Une trajectoire générique comprend donc, dans le plan orbital, une composante périodique (liée aux racines imaginaires pures), une composante amortie (liée à la racine réelle positive), et une composante instable. Pour une position δX, δY donnée, il est toujours possible de choisir une vitesse telle que les deux vecteurs propres aux racines réelles ne contribuent pas à la solution correspondante. La trajectoire obtenue est alors périodique, la période étant donnée par la racine complexe. Une telle solution n'est cependant pas stable. Un écart de trajectoire infime va en réalité rajouter à la trajectoire une composante instable, qui va peu à peu éloigner et faire diverger la trajectoire de sa composante périodique. On dit que la trajectoire obtenue n'est pas dynamiquement stable. Ceci est une généralisation du fait qu'un objet situé exactement sur un point de Lagrange instable est dans une situation instable : un petit écart à cette position d'équilibre, inéluctablement généré par les perturbations causées par les autres corps du système, finira par éloigner l'objet de sa position initiale. La même chose se produit pour des trajectoires situées autour du point d'équilibre instable.
Pertinence du concept
Le calcul ci-dessus fait référence à une configuration où les deux corps du système sont en orbite circulaire. Néanmoins, le concept de point de Lagrange vaut pour tout type d'orbite, y compris elliptique. On peut donc définir ces points dans tout système à deux corps liés gravitationnellement. En revanche, les trajectoires, stables ou instables, autour des différents points de Lagrange dépendent explicitement de la circularité ou non de l'orbite des deux corps du système.
Utilisation dans les missions spatiales

L'étude mathématique des points de Lagrange, ainsi que de leurs propriétés mathématiques, telles que les Variétés invariantes (en) associées, a été exploitée pour concevoir des missions de sondes spatiales dans le système solaire. Pour des missions comme Rosetta, Voyager ou Galileo, la vitesse relative de la sonde par rapport aux corps considérés est suffisamment élevée pour que l’approximation, considérant que les orbites képlériennes ne sont que peu perturbées par les autres corps au sein de la sphère d’influence, soit valide. Cependant, dès qu’on considère des vitesses et des poussées faibles, une approximation plus fine est nécessaire.
Le théorème de Liapounov-Poincaré assure de l’existence d’une famille d’orbites périodiques[Quoi ?] autour de ces points d’équilibre. Les orbites périodiques planaires sont alors appelées « orbites de Liapounov », alors que dans le cas tridimensionnel, elles sont appelées en fonction de leurs propriétés topologiques, soit « orbites de halo », soit « orbites de Lissajous ». Ce type d’orbites périodiques autour des points de Lagrange a déjà été utilisé dans la construction de missions réelles telles que la mission SoHO.
De ces orbites périodiques autour des points de Lagrange sont issues des variétés invariantes (tubes de Conley-McGee) qui sont des séparatrices de la dynamique et qui en ce sens peuvent être considérées comme des courants gravitationnels. De plus en plus, ces courants sont utilisés pour la conception de missions, notamment le réseau de transport interplanétaire (ITN)[7].

Les Points de Lagrange sont utilisés pour répondre à des besoins spécifiques de certaines missions spatiales.
Point de Lagrange L1
Le point de Lagrange L1 du système Terre-Soleil, situé entre la Terre et le Soleil (bien que beaucoup plus proche de notre planète), permet d'observer le Soleil sans interférence ni ombrage de la Terre et de la Lune. Il est possible d'y mesurer l'activité solaire (éruptions, cycles, vent solaire) sans que celle-ci ne soit affectée par la magnétosphère terrestre. C'est la position idéale pour des missions de météorologie spatiale comme celle remplie par SoHO et ACE.
C'est également le point L1 qui est choisi pour positionner le futur télescope NEO Surveyor pour pouvoir observer une grande portion de l'espace dans lequel circulent les géocroiseurs.
Point de Lagrange L2
Le point de Lagrange L2 du système Terre-Soleil permet de bénéficier d'une grande stabilité thermique tout en étant situé suffisamment près de la Terre (1,5 million de kilomètres) pour que les données collectées puissent y être transférées avec un débit élevé. Il est utilisé en particulier par les grands observatoires astronomiques spatiaux lancés dans les décennies 2010 et 2020 : Planck[8], James-Webb[8], Herschel[8], WMAP[8], Gaia, Euclid.
En ce qui concerne le télescope James-Webb, le point L2 est idéal pour observer les objets célestes en infra-rouge, car privés de lumière et de chaleur du soleil, de la terre et de la lune, ses instruments d'observation sont toujours laissés à -233 °C, ce qui est nécessaire pour sa fonction[8].
Le point de Lagrange L2 du système Terre-Lune a été utilisé pour la première fois en 2018, comme un intermédiaire Terre-Lune, par le satellite chinois Queqiao. Ce satellite de télécommunication peut ainsi retransmettre vers la Terre les données collectées par la sonde spatiale Chang'e 4 posée sur la face cachée de la Lune.

Dans le Système solaire
Troyens
Les points L4 et L5 sont généralement stables, aussi on y trouve de nombreux corps naturels, dits troyens :
- dans le système Soleil-Jupiter, on recense (en 2011) environ 5 000 astéroïdes aux points L4 et L5 ;
- dans le système Soleil-Neptune, huit ;
- dans le système Soleil-Mars, quatre ;
- dans le système Saturne-Téthys, les points L4 et L5 sont occupés par Télesto et Calypso, respectivement ;
- dans le système Saturne-Dioné, Hélène et Pollux occupent ces points.
Curieusement, il semblerait que le système Soleil-Saturne ne soit pas en mesure d'accumuler des troyens du fait des perturbations joviennes.
Dans le système Soleil-Terre, on connait depuis le un troyen au point L4, l'astéroïde 2010 TK7, qui mesure 300 mètres de diamètre[9],[10],[11]. Un deuxième troyen a été découvert en décembre 2020, d'un diamètre de l'ordre du kilomètre[12]. Certains astronomes soulignent que cet objet pourrait représenter un risque comparable aux géocroiseurs[13]. Ces auteurs proposent également que l'impacteur géant supposément à l'origine de la Lune (Théia) aurait stationné un temps sur le point L4 ou L5 et accumulé de la masse avant d'en être éjecté sous l'action des autres planètes.
Applications
Les points L1 et L2 sont des équilibres instables, ce qui les rend utilisables dans le cadre de missions spatiales : on n'y trouve pas ou peu de corps naturels, et un équilibre dynamique peut y être maintenu pour une consommation de carburant raisonnable (le champ gravitationnel étant faible dans leur voisinage).
Système Soleil-Terre
Les principaux avantages de ces positions, en comparaison des orbites terrestres, sont leur éloignement de la Terre et leur exposition au Soleil constante dans le temps. Le point L1 se prête particulièrement à l'observation du Soleil et du vent solaire. Ce point a été occupé pour la première fois en 1978 par le satellite ISEE-3, puis par le satellite LISA Pathfinder[14] en 2016 (fin de mission en 2017). Le point est actuellement occupé par les satellites SoHO (fin de mission prévue fin 2025), DSCOVR (mission de la NOAA en cours depuis 2015) et Advanced Composition Explorer (fin de mission prévue fin 2024).
Le point L2 est à l'inverse particulièrement intéressant pour les missions d'observation du cosmos, qui embarquent des instruments de grande sensibilité devant être détournés de la Terre et de la Lune, et fonctionnant à très basse température. Son orbite a été utilisée par les satellites Herschel (fin de mission en 2013), Planck (fin de mission en 2013), WMAP (fin de mission en 2010). Il est actuellement occupé par les télescopes spatiaux Gaia (mission en cours jusqu'à fin 2025[15]), James Webb (depuis [16]) et Euclid (juillet 2023) que doit rejoindre Nancy-Grace-Roman (vers 2025).
Système Terre-Lune
Dans le cadre de la mission chinoise Chang'e 4, sonde spatiale lunaire ayant atterri en 2019 sur la face cachée de la lune, un satellite relais Quequio a été placé au point L2 afin d'assurer les communications entre la Terre et la sonde.
Il a été un temps envisagé de placer un télescope spatial au point L4 ou L5 du système Terre-Lune, mais cette option a été abandonnée après que des nuages de poussière y ont été observés.
En science-fiction
En science-fiction, de par leur stabilité, les points L4 et L5 du système Terre-Lune abritent souvent de gigantesques colonies spatiales, comme dans le roman Vendredi, de Robert A. Heinlein, où ceux-ci sont mentionnés dès l'introduction sous le nom de Ell-4 et Ell-5.
Les auteurs de science-fiction et de bande dessinée aiment également placer une Anti-Terre au point L3. Cette idée est cependant irréaliste : les points de Lagrange n'ont de sens que pour un objet de masse négligeable par rapport aux deux éléments du système, ce qui n'est pas le cas d'une planète jumelle.
Parmi les auteurs ayant utilisé ces points dans leurs récits, John Varley envisage dans plusieurs de ses romans et nouvelles l'installation de colonies aux points de Lagrange de l'ensemble Terre-Lune, tirant parti du fait qu'un objet de faible masse n'aurait besoin d'aucune énergie pour maintenir sa position relative aux deux astres. C'est le cas notamment dans sa série dite de la Trilogie de Gaïa où certains personnages principaux des deux derniers tomes viennent d'une de ces colonies, « le Covent »,
On les trouve aussi, de manière souvent secondaire, dans les récits (romans et nouvelles) qui se situent dans le contexte de la série Les Huit Mondes. Dans le roman Gens de la Lune notamment, le point L5 est le lieu d'assemblage du vaisseau spatial Robert Anson Heinlein censé se lancer dans un voyage intersidéral, avant que le projet soit abandonné et la carcasse du vaisseau remisée dans une décharge sur la Lune.
Dans les diverses œuvres des univers de Gundam, les colonies spatiales sont souvent situées aux points de Lagrange[17], ce qui en fait des positions stratégiques importantes dans ces conflits orbitaux.
Dans Rupture dans le réel, de Peter F. Hamilton, un vaisseau spatial traqué par plusieurs vaisseaux ennemis leur échappe via un point de Lagrange pour pouvoir faire un saut (de type hyperspatial même si le terme n'est pas utilisé) car c'est le seul endroit proche où la gravité est quasi nulle. Son capitaine Joshua Calvert est par la suite surnommé Lagrange Calvert à la suite de cet exploit.
Dans le film 2010 : L'Année du premier contact de Peter Hyams (1984) (qui fait suite à 2001, l'Odyssée de l'espace), le monolithe gigantesque dont la nature reste mystérieuse est présenté comme positionné sur un point de Lagrange entre Jupiter et une de ses lunes, Io.
Dans le jeu vidéo Star Citizen, des stations relais qui permettent de se ravitailler et de faire un peu de commerce sont situées aux Points de Lagrange de chaque planètes. Elles se nomment CRU L1 à CRU L5 pour la planète Crusader, HUR L1 à HUR L5 pour Hurston, ARC L1 à ARC L5 pour ArcCorp et MIC L1 à MIC L5 pour MicroTech[18].
Dans une des fins de Cyberpunk 2077, on apprend que la luxueuse station spatiale touristique Crystal Palace se trouve au point de Lagrange L1 entre la Terre et la Lune.
Notes et références
- ↑ Essai sur le Problème des Trois Corps[PDF], ltas-vis.ulg.ac.be.
- ↑ Géométrie de Roche, Jean-Marie Hameury, Observatoire de Strasbourg [PDF], astro.u-strasbg.fr.
- ↑ Bernard Bonnard, Ludovic Faubourg et Emmanuel Trélat, Mécanique céleste et contrôle des véhicules spatiaux, Berlin, Springer, coll. « Mathématiques et applications », , XIV-276 p. (ISBN 978-3-540-28373-7, BNF 40153166, lire en ligne), p. 73 (lire en ligne) sur Google Livres (consulté le 25 juillet 2014).
- ↑ (en) « What are Lagrange points? », sur esa.int (consulté le ).
- ↑ Zakir F. Seidov, « The Roche Problem: Some Analytics », The Astrophysical Journal, vol. 603, no 1, , p. 283–284 (DOI 10.1086/381315, Bibcode 2004ApJ...603..283S, arXiv astro-ph/0311272, S2CID 16724058)
- ↑ Si l'on définit q comme le rapport de la plus petite masse à la totale, seules les valeurs de q inférieures à 0,5 ont un sens, puisque les valeurs plus grandes correspondent au rapport de la plus grande masse à la masse totale.
- ↑ (en) Maxime Chupin, Interplanetary transfers with low consumption using the properties of the restricted three body problem (thèse de doctorat en mathématiques appliquées), , 172 p. (présentation en ligne, lire en ligne [PDF]), p. 6.
- ↑ a b c d e et f James Webb Space Telescope par Goddard Space Flight Center, Webb Orbit (en)[lire en ligne] (consulté le 10 décembre 2023)
- ↑ (en) Martin Connors, Paul Wiegert et Christian Veillet, « Earth's trojan asteroid », Nature, vol. 475, no 7357, , p. 481-483 (DOI 10.1038/nature10233, Bibcode 2011Natur.475..481C, lire en ligne [PDF], consulté le ).
- ↑ (en) Whitney Clavin et Trent J. Perrotto, « NASA's WISE mission finds first trojan asteroid sharing Earth's orbit », sur NASA, mis en ligne le 27 juillet 2011 (consulté le ).
- ↑ Philippe Ribeau-Gésippe, « Un nouveau satellite pour la Terre : Le premier satellite troyen de la Terre a été découvert », Pour la Science, no 407, , p. 6 (lire en ligne, consulté le ).
- ↑ (en) T. Santana-Ros, M. Micheli, L. Faggioli et R. Cennamo, « Orbital stability analysis and photometric characterization of the second Earth Trojan asteroid 2020 XL5 », Nature Communications, vol. 13, no 1, , p. 447 (ISSN 2041-1723, DOI 10.1038/s41467-022-27988-4, lire en ligne, consulté le ).
- ↑ (en) Do gravity holes harbour planetary assassins?, New Scientist.
- ↑ (en) « LISA Pathfinder's journey through space - annotated », sur sci.esa.int, Agence spatiale européenne (consulté le ).
- ↑ « Gaia - Fact Sheet », sur ESA Science & Technology (consulté le ).
- ↑ https://blogs.nasa.gov/webb/2022/01/21/webbs-journey-to-l2-is-nearly-complete/ consulté le 26 jan. 2022.
- ↑ (en) « Lagrange Points », The Gundam Wiki, (lire en ligne, consulté le ).
- ↑ « Star Citizen : Les stations spatiales du patch 3.6 », sur Millenium FR (consulté le )
- Grégory Archambeau, Étude de la dynamique autour des points de Lagrange, Orsay, Université Paris XI, , X-114 p., lire en ligne[PDF] sur [1]
- Maxime Chupin, Interplanetary transfers with lowconsumption using the properties of therestricted three body problem, Paris, Université Pierre-et-Marie-Curie, , XXVIII-171 p., lire en ligne[PDF] sur [2]
- (en) Richard Fitzpatrick, Analytical Classical Dynamics, cours donné à l'Université du Texas à Austin Voir en ligne (versions pdf et html).
Voir aussi
Sur les autres projets Wikimedia :
- Point de Lagrange, sur Wikimedia Commons
- point de Lagrange, sur le Wiktionnaire
Articles connexes
Liens externes
- Notices d'autorité
 :
: - BnF (données)
- Ressource relative à la littérature
 :
: - The Encyclopedia of Science Fiction
- Notices dans des dictionnaires ou encyclopédies généralistes
 :
: - Britannica
- Gran Enciclopèdia Catalana
- Store norske leksikon
- (en) Librairie du Congrès
 Portail de l’astronomie
Portail de l’astronomie  Portail de l’astronautique
Portail de l’astronautique


























































































































![{\displaystyle q\in \left]{\frac {1}{2}}-{\frac {1}{2}}{\sqrt {\frac {23}{27}}},{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {23}{27}}}\right[\simeq ]0,\!03852,0,\!96148[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1393380f327b6005bbdcd729db790187c7c93cc4)
































































