Petit rhombicosidodécaèdre

Petit rhombicosidodécaèdre

Éléments

Faces	Arêtes	Sommets
62 triangles, carrés et pentagones	120	60 de degré 4

Données clés

Type	Solide d'Archimède
Caractéristique	2
Propriétés	Semi-régulier et convexe
Groupe de symétrie	Ih
Dual	Hexacontaèdre trapézoïdal

modifier

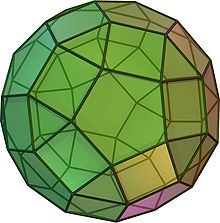
Le petit rhombicosidodécaèdre est un solide d'Archimède. Il possède 20 faces triangulaires régulières, 30 faces carrées régulières, 12 faces pentagonales régulières, 60 sommets et 120 arêtes.

Le nom rhombicosidodécaèdre fait référence au fait que les 30 faces carrées sont placées dans les mêmes plans que les 30 faces du triacontaèdre rhombique qui est le dual de l'icosidodécaèdre.

Il peut aussi être appelé un dodécaèdre étendu ou un icosaèdre étendu à partir des opérations de troncature du solide uniforme.

Relations géométriques

Si vous étendez un icosaèdre en déplaçant les faces de l'origine d'une certaine distance, sans changer l'orientation ou la taille des faces et que vous faites la même chose à son dual, le dodécaèdre et que vous remplissez les trous carrés dans le résultat, vous obtenez un petit rhombicosidodécaèdre. Par conséquent, il possède le même nombre de triangles qu'un icosaèdre et le même nombre de pentagones qu'un dodécaèdre, avec un carré pour chaque côté d'arête.

Les kits Zome pour fabriquer des dômes géodésiques et d'autres polyèdres utilisent des boules fendues comme connecteurs. Les boules sont des petits rhombicosidodécaèdres "développés", avec les carrés remplacés par des rectangles. Le développement est choisi de telle sorte que les rectangles résultants sont des rectangles d'or.

Coordonnées cartésiennes

Les coordonnées cartésiennes pour les sommets d'un petit rhombicosidodécaèdre centré à l'origine sont

${\displaystyle (\pm 1,\pm 1,\pm \varphi ^{3})}$,

${\displaystyle (\pm \varphi ^{3},\pm 1,\pm 1)}$,

${\displaystyle (\pm 1,\pm \varphi ^{3},\pm 1)}$,

${\displaystyle (\pm \varphi ^{2},\pm \varphi ,\pm 2\varphi )}$,

${\displaystyle (\pm 2\varphi ,\pm \varphi ^{2},\pm \varphi )}$,

${\displaystyle (\pm \varphi ,\pm 2\varphi ;,\pm \varphi ^{2})}$,

${\displaystyle (\pm (2+\varphi ),0,\pm \varphi ^{2})}$,

${\displaystyle (\pm \varphi ^{2},\pm (2+\varphi ),0)}$,

${\displaystyle (0,\pm \varphi ^{2},\pm (2+\varphi ))}$,

où ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ est le nombre d'or. En utilisant ${\displaystyle \varphi ^{2}=\varphi +1}$, on vérifie que tous les sommets sont sur une sphère centrée à l'origine.

Voir aussi

• Dodécaèdre
• Grand rhombicosidodécaèdre
• Icosaèdre
• Icosidodécaèdre
• Petit rhombicuboctaèdre

Références

• Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, (ISBN 0-486-23729-X)

Liens externes

• (en) Les polyèdres uniformes
• (en) Les polyèdres en réalité virtuelle L'encyclopédie des Polyèdres

• Portail de la géométrie