Loi logarithmique

Cet article est une ébauche concernant les probabilités et la statistique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Logarithmique
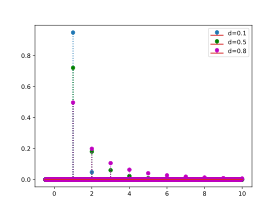Fonction de masse
Fonction de répartition
Paramètres	${\displaystyle p\in \left]0,1\right[\!}$ ${\displaystyle q=1-p}$
Support	${\displaystyle k\in \{1,2,3,\dots \}\!}$
Fonction de masse	${\displaystyle {\frac {-1}{\ln q}}\;{\frac {\;p^{k}}{k}}\!}$
Fonction de répartition	${\displaystyle 1+{\frac {\mathrm {B} _{p}(k+1,0)}{\ln q}}\!}$
Espérance	${\displaystyle {\frac {-1}{\ln q}}\;{\frac {p}{q}}\!}$
Mode	${\displaystyle 1}$
Variance	${\displaystyle -p\;{\frac {p+\ln q}{q^{2}\,\ln ^{2}q}}\!}$
Fonction génératrice des moments	${\displaystyle {\frac {\ln(q\,\exp(t))}{\ln q}}\!}$
Fonction caractéristique	${\displaystyle {\frac {\ln(q\,\exp(i\,t))}{\ln q}}\!}$
Fonction génératrice des probabilités	${\displaystyle {\frac {\ln(1-pt)}{\ln q}}}$
modifier

En probabilité et en statistiques, la loi logarithmique est une loi de probabilité discrète, dérivée du développement de Taylor de la fonction logarithme népérien. En anglais, cette loi est plutôt appelée logarithmic series distribution ou log-series distribution, pour éviter la confusion avec les lois dont les variables sont les logarithmes de variables suivant d'autres lois, comme la loi log-normale.

Définition

On part du développement en série entière suivant :

${\displaystyle -\ln(1-p)=p+{\frac {p^{2}}{2}}+{\frac {p^{3}}{3}}+\cdots .}$

pour ${\displaystyle 0<p<1}$. On peut en déduire l'identité qui suit :

${\displaystyle \sum _{k=1}^{\infty }{\frac {-1}{\ln(1-p)}}\;{\frac {p^{k}}{k}}=1.}$

On peut en tirer la loi de probabilité d'une variable aléatoire X distribuée selon une loi logarithmique, notée Log(p) :

${\displaystyle f(k;p)=P(X=k)={\frac {-1}{\ln(1-p)}}\;{\frac {p^{k}}{k}}}$

pour ${\displaystyle k\geq 1}$, et où ${\displaystyle 0<p<1}$.

La fonction de répartition associée est

${\displaystyle F(k)=1+{\frac {\mathrm {B} _{p}(k+1,0)}{\ln(1-p)}}}$

où ${\displaystyle \mathrm {B} }$ est la fonction bêta incomplète.

Relations avec d'autres lois de probabilité

Pour p proche de 0,5, la loi logarithmique tend vers la loi géométrique de paramètre p^[1].

Un mélange loi de Poisson- loi logarithmique possède une loi binomiale négative: si ${\displaystyle N}$ est une variable aléatoire tirée selon une loi de Poisson et que ${\displaystyle X_{i}}$, ${\displaystyle i}$ = 1, 2, 3, ... est une série infinie de variables identiquement et indépendamment distribuées selon une loi Log(p), alors

${\displaystyle \sum _{n=1}^{N}X_{i}}$

est distribuée selon une loi binomiale négative.

Applications

Ronald Fisher a utilisé cette loi dans certains modèles de la génétique des populations.

Références

• (en) Norman L. Johnson, Adrienne W. Kemp et Samuel Kotz, Univariate Discrete Distributions, Wiley-Interscience, p. 285-304 (ISBN 0471272469), « 7 »
• (en) Eric W. Weisstein, « Log-Series Distribution », sur MathWorld

• Portail des probabilités et de la statistique