Markovljev proces odlučivanja

U matematici, Markovljev proces odlučivanja (MDP) je stohastički kontrolni proces sa diskretnim vremenom. On pruža matematički okvir za modelovanje donošenja odluka u situacijama u kojima su ishodi delimično randomni, a delom pod kontrolom donosioca odluka. MDP-ovi su korisni za proučavanje problema optimizacije rešenih dinamičkim programiranjem. MDP-ovi su bili poznati bar još 1950-ih;^[1] jezgro istraživanja o Markovljevim procesima odlučivanja je rezultat knjige Ronalda Hauarda iz 1960. Dinamičko programiranje i Markovljevi procesi.^[2] Oni se koriste u mnogim disciplinama, uključujući robotiku, automatsku kontrolu, ekonomiju i proizvodnju. Naziv MDP-a potiče od ruskog matematičara Andreja Markova jer su oni produžetak Markovljevih lanaca.

U svakom vremenskom koraku, proces je u nekom stanju ${\displaystyle s}$, a donosilac odluke može izabrati bilo koju radnju ${\displaystyle a}$ koja je dostupna u stanju ${\displaystyle s}$. Proces reaguje u sledećem vremenskom koraku tako što se randomno kreće u novo stanje ${\displaystyle s'}$ i daje donosiocu odluke odgovarajuću nagradu ${\displaystyle R_{a}(s,s')}$.

Izabrana radnja utiče na verovatnoću da proces pređe u svoje novo stanje ${\displaystyle s'}$. Konkretno, data je funkcijom prelaza stanja ${\displaystyle P_{a}(s,s')}$. Dakle, sledeće stanje ${\displaystyle s'}$ zavisi od trenutnog stanja ${\displaystyle s}$ i akcije donosioca odluke ${\displaystyle a}$. Ali s obzirom na ${\displaystyle s}$ i ${\displaystyle a}$, uslovno je nezavisno od svih prethodnih stanja i radnji; drugim rečima, tranzicije stanja MDP-a zadovoljavaju Markovljevo svojstvo.

Markovljevi procesi odlučivanja su produžetak Markovljevih lanaca; razlika je dodavanje akcija (omogućavanje izbora) i nagrada (davanje motivacije). Suprotno tome, ako postoji samo jedna radnja za svako stanje (npr. „čekaj“) i sve nagrade su iste (npr. „nula“), proces Markovljevog odlučivanja se svodi na Markovljev lanac.

Definicija

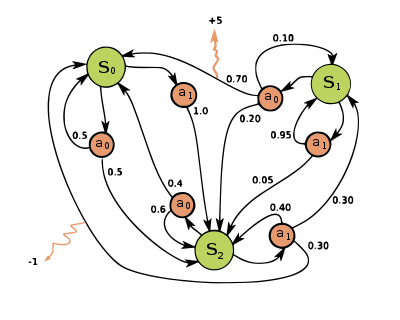
Markovljev proces odlučivanja je 4-orka ${\displaystyle (S,A,P_{a},R_{a})}$, gde je:

• ${\displaystyle S}$ je skup stanja koji se naziva prostor stanja,
• ${\displaystyle A}$ je skup radnji koje se nazivaju prostor radnje (alternativno, ${\displaystyle A_{s}}$ je skup akcija dostupnih iz stanja ${\displaystyle s}$),
• ${\displaystyle P_{a}(s,s')=\Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)}$ je verovatnoća da će radnja ${\displaystyle a}$ u stanju ${\displaystyle s}$ u vreme ${\displaystyle t}$ dovesti do stanja ${\displaystyle s'}$ u vreme ${\displaystyle t+1}$,
• ${\displaystyle R_{a}(s,s')}$ je neposredna nagrada (ili očekivana trenutna nagrada) dobijena nakon prelaska iz stanja ${\displaystyle s}$ u stanje ${\displaystyle s'}$, zbog radnje ${\displaystyle a}$

Prostori stanja i radnje mogu biti konačni ili beskonačni, na primer skup realnih brojeva. Neki procesi sa prebrojivo beskonačnim prostorima stanja i delovanja mogu se svesti na one sa konačnim prostorima stanja i delovanja.^[3]

Funkcija politike ${\displaystyle \pi }$ je (potencijalno probabilističko) mapiranje iz prostora stanja (${\displaystyle S}$) u prostor delovanja (${\displaystyle A}$).

Cilj optimizacije

Cilj u Markovljevom procesu odlučivanja je da se pronađe dobra „politika“ za donosioca odluka: funkcija ${\displaystyle \pi }$ koja određuje radnju ${\displaystyle \pi (s)}$ koju će donosilac odluke izabrati kada je u stanju ${\displaystyle s}$. Nakon što se Markovljev proces odlučivanja kombinuje sa politikom na ovaj način, ovo fiksira radnju za svako stanje i rezultirajuća kombinacija se ponaša kao Markovljev lanac (pošto je radnja izabrana u stanju ${\displaystyle s}$ potpuno određena sa ${\displaystyle \pi (s)}$ i ${\displaystyle \Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)}$ se svodi na ${\displaystyle \Pr(s_{t+1}=s'\mid s_{t}=s)}$, Markovljevu prelaznu matricu).

Cilj je odabrati politiku ${\displaystyle \pi }$ koja će maksimizovati neku kumulativnu funkciju randomnih nagrada, obično očekivanu sniženu sumu u potencijalno beskonačnom horizontu:

${\displaystyle E\left[\sum _{t=0}^{\infty }{\gamma ^{t}R_{a_{t}}(s_{t},s_{t+1})}\right]}$ (gde se bira ${\displaystyle a_{t}=\pi (s_{t})}$, i.e. radnje koje daje politika). A očekivanje se preuzima preko ${\displaystyle s_{t+1}\sim P_{a_{t}}(s_{t},s_{t+1})}$

gde je ${\displaystyle \ \gamma \ }$ faktor popusta koji zadovoljava ${\displaystyle 0\leq \ \gamma \ \leq \ 1}$, što je obično blizu 1 (na primer, ${\displaystyle \gamma =1/(1+r)}$ za neku diskontnu stopu r). Niži diskontni faktor motiviše donosioca odluka da favorizuje preduzimanje radnji rano, umesto da ih odlaže na neodređeno vreme.

Politika koja maksimizira gornju funkciju naziva se optimalna politika i obično se označava sa ${\displaystyle \pi ^{*}}$. Određeni MDP može imati više različitih optimalnih politika. Zbog Markovljevog svojstva, može se pokazati da je optimalna politika funkcija trenutnog stanja, kao što je pretpostavljeno gore.

Simulatorski modeli

U mnogim slučajevima, teško je eksplicitno predstaviti distribuciju verovatnoće prelaza, ${\displaystyle P_{a}(s,s')}$. U takvim slučajevima, simulator se može koristiti za implicitno modelovanje MDP-a pružanjem uzoraka iz distribucija prelaza. Jedan uobičajeni oblik implicitnog MDP modela je epizodični simulator okruženja koji se može pokrenuti iz početnog stanja i donosi naknadno stanje i nagradu svaki put kada primi akcioni unos. Na ovaj način se mogu proizvesti putanje stanja, radnji i nagrada, koje se često nazivaju epizodama.

Drugi oblik simulatora je generativni model, simulator sa jednim korakom koji može da generiše uzorke sledećeg stanja i nagradi za bilo koje stanje i radnju.^[4] (Treba imati na umu da je ovo drugačije značenje od termina generativni model u kontekstu statističke klasifikacije.) U algoritmima koji se izražavaju pomoću pseudokoda, ${\displaystyle G}$ se često koristi za predstavljanje generativnog modela. Na primer, izraz ${\displaystyle s',r\gets G(s,a)}$ može da označi akciju uzorkovanja iz generativnog modela gde su ${\displaystyle s}$ i ${\displaystyle a}$ su trenutno stanje i radnja, a ${\displaystyle s'}$ i ${\displaystyle r}$ su novo stanje i nagrada. U poređenju sa epizodnim simulatorom, generativni model ima prednost u tome što može dati podatke iz bilo kog stanja, a ne samo one na koje se naiđe na putanji.

Ove klase modela formiraju hijerarhiju informacionog sadržaja: eksplicitni model trivijalno daje generativni model kroz uzorkovanje iz distribucija, a ponovljena primena generativnog modela daje epizodični simulator. U suprotnom smeru, moguće je naučiti samo približne modele putem regresije. Tip modela koji je dostupan za određeni MDP igra značajnu ulogu u određivanju koji su algoritmi rešenja odgovarajući. Na primer, algoritmi za dinamičko programiranje opisani u sledećem odeljku zahtevaju eksplicitan model, a Monte Karlo pretraga stabla zahteva generativni model (ili epizodični simulator koji se može kopirati u bilo kom stanju), dok većina algoritama podržanog učenja zahteva samo epizodni simulator.

Reference

Literatura

Spoljašnje veze

• Learning to Solve Markovian Decision Processes by Satinder P. Singh