Fază (mecanică statistică)

În mecanica statistică, se numește fază o stare microscopică a unui sistem termodinamic la un moment dat, caracterizată prin valorile coordonatelor și a impulsurilor canonice ale punctelor materiale care îl alcătuiesc. O imagine geometrică utilă, pentru un sistem cu n grade de libertate, se obține considerând coordonatele q₁, q₂, ... q_n și impulsurile p₁, p₂, ... p_n drept coordonatele unui punct într-un spațiu 2n-dimensional numit spațiul fazelor. O fază este reprezentată de un punct în spațiul fazelor, iar evoluția în timp a sistemului (dependența de timp a coordonatelor și impulsurilor) urmărește o curbă continuă numită traiectoria punctului reprezentativ. Întrucât starea sistemului la un moment oarecare este determinată, prin ecuațiile canonice ale lui Hamilton, de starea sa la un moment anterior, o traiectorie este complet determinată de unul din punctele ei; prin fiecare punct din spațiul fazelor trece o singură traiectorie.

Această terminologie a fost introdusă de Gibbs în anul 1901.

Considerații de mecanică clasică

Pentru înțelegerea conceptelor fază, spațiul fazelor, traiectorie în spațiul fazelor, punct reprezentativ , este utilă tratarea celui mai simplu caz, acela al unui sistem cu un singur grad de libertate. Din punct de vedere dinamic, un asemenea sistem este descris de o singură ecuație diferențială de tipul: ${\displaystyle \scriptstyle {\ddot {q}}=f(q)}$, ecuație care este echivalentă cu sistemul de două ecuații diferențiale parametrice:

${\displaystyle {\dot {q}}=p,{\dot {p}}=f(q)}$

Dacă se consideră planul de coordonate ${\displaystyle \scriptstyle (q,\,p)}$, acesta va reprezenta mulțimea tuturor stărilor dinamice ale sistemului cu un singur grad de libertate, numit planul fazelor iar un punct, de coordonate ${\displaystyle \scriptstyle (q_{i},p_{i})}$ din acest plan, reprezintă starea ${\displaystyle \scriptstyle (i)}$ a sistemului. Membrul drept al sistemului de mai sus, definește un câmp de vectori pe planul fazelor, numit câmpul vectorial al vitezelor. Soluția sistemului este o mișcare, definit analitic prin funcționala^{⁠(fr)[traduceți]} ${\displaystyle \scriptstyle \phi :\mathbb {R} \rightarrow {\mathbb {R} }^{2}}$ a stării sistemului în planul fazelor pentru care viteza de mișcare a stării este egală în fiecare moment cu vectorul vitezei în acel punct (în care se află starea la momentul considerat. Soluția ${\displaystyle \scriptstyle \phi }$ este definită pe toată semiaxa pozitivă (axa timpului); pentru „comoditate”, se poate extinde definirea pe întreaga axă reală.

Imaginea unei asemenea aplicații se numește orbită sau traiectorie în planul fazelor. O orbită este determinată de ecuațiile parametrice:

${\displaystyle q=\phi _{1}(t),p=\phi _{2}(t),\,\phi _{2}(t)={\dot {\phi }}_{1}(t).}$

Unde ${\displaystyle \scriptstyle \phi _{1}(t)}$ și ${\displaystyle \scriptstyle \phi _{2}(t)}$ sunt funcții scalare de clasă ${\displaystyle \scriptstyle C^{1}(\mathbb {R} _{+})}$. Folosind teoria ecuațiilor diferențiale ordinare se demonstrează că prin oricare stare (punct al planului fazelor) trece o orbită și numai una singură. O orbită se poate reduce la un singur punct, numit poziție de echilibru în care vectorul viteză în planul fazelor este nul. Pentru un sistem cu un grad de libertate, legea conservării energiei mecanice permite ușor determinarea orbitelor. Pe fiecare orbită, valoarea energiei totale este constantă, motiv pentru care fiecare orbită (traiectorie) reprezintă o mulțime unică de stări (subvarietate reprezentat prin puncte ale planului fazelor) de nivel constant al energiei mecanice: ${\displaystyle \scriptstyle E(q,p)=h=const.}$

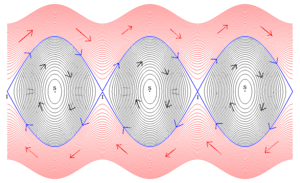
Planul fazelor pentru un oscilator armonic linear

Bibliografie

• Țițeica, Șerban: Elemente de mecanică statistică, Editura Tehnică, București, 1956.
• Arnold, V. I.: Metodele matematice ale mecanicii clasice (traducere din limba rusă), Editura Științifică și Enciclopedică, București, 1980.
• Caius Iacob: Mecanică teoretică, Editura Didactică și Pedagogică, București, 1980.