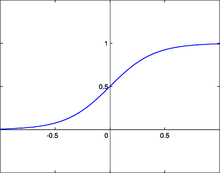
シグモイド関数

シグモイド関数（シグモイドかんすう、英: sigmoid function）は、次の式

${\displaystyle \varsigma _{a}(x)={\frac {1}{1+e^{-ax}}}={\frac {\tanh(ax/2)+1}{2}}}$

で表される実関数である。ここで、${\displaystyle a}$ をゲイン (gain) と呼ぶ。 シグモイド関数は、生物の神経細胞が持つ性質をモデル化したものとして用いられる。

狭義のシグモイド関数は、ゲインを1とした、標準シグモイド関数（英: standard sigmoid function）

${\displaystyle \varsigma _{1}(x)={\frac {1}{1+e^{-x}}}={\frac {\tanh(x/2)+1}{2}}}$

を指す。

名称

シグモイド（英: sigmoid）とは、シグモイド曲線（英: sigmoid curve）ともいい、ギリシャ文字のシグマ（語中では σ だがここでは語末形の ς のこと）に似た形と言う意味である。ただし、単にシグモイドまたはシグモイド曲線と言った場合は、シグモイド関数と似た性質を持つς型の関数（累積正規分布関数、ゴンペルツ関数、グーデルマン関数など）を総称するのが普通である。

標準シグモイド関数はロジット (logit) の逆関数であり、これになぞらえて統計処理の数値計算ライブラリでは標準シグモイド関数を expit 関数と呼んでいるものもある。

性質

${\displaystyle (-\infty ,\infty )\rightarrow (0,1)}$ の単調増加連続関数で、後述するただ1つの変曲点を持つ。

${\displaystyle y=0}$ と ${\displaystyle y=1}$ を漸近線に持ち、

${\displaystyle {\begin{aligned}\lim _{x\rightarrow \infty }\varsigma _{a}(x)&=1\\\lim _{x\rightarrow -\infty }\varsigma _{a}(x)&=0\\\lim _{x\rightarrow \pm \infty }\varsigma _{a}'(x)&=0\end{aligned}}}$

である。

また、${\displaystyle x=0}$ では、

${\displaystyle {\begin{aligned}\varsigma _{a}(0)&={\frac {1}{2}}\\\varsigma _{a}'(0)&={\frac {a}{4}}\\\varsigma _{a}''(0)&=0\end{aligned}}}$

である。つまり、変曲点は ${\displaystyle (0,{\frac {1}{2}})}$ である。 シグモイド関数のグラフは、${\displaystyle (0,{\frac {1}{2}})}$ を中心に点対称である。すなわち、${\displaystyle \varsigma _{a}(x)-{\frac {1}{2}}}$ は奇関数であり、${\displaystyle \varsigma _{a}(-x)=1-\varsigma _{a}(x)}$ を満たす。

逆関数は、

${\displaystyle \varsigma _{a}^{-1}(y)={\frac {1}{a}}\ln \left({\frac {y}{1-y}}\right)={\frac {1}{a}}\operatorname {logit} y}$

と、ロジット関数で表せる。特に、標準シグモイド関数とロジット関数は互いに逆関数である。

導関数と二階導関数は、

${\displaystyle {\begin{aligned}\varsigma _{a}'(x)&={\frac {ae^{-ax}}{(1+e^{-ax})^{2}}}=a\varsigma _{a}(x)\{1-\varsigma _{a}(x)\}\\\varsigma _{a}''(x)&=a^{2}\varsigma _{a}(x)\{1-\varsigma _{a}(x)\}\{1-2\varsigma _{a}(x)\}\end{aligned}}}$

と、シグモイド関数自身を使って簡潔に表せる。

自然対数と絡んで微分するとこのようになる。

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\ln(\varsigma _{a}(x))&=a\varsigma _{a}(-x)=a(1-\varsigma _{a}(x))\\{\frac {d}{dx}}\ln(1-\varsigma _{a}(x))&=-a\varsigma _{a}(x)\end{aligned}}}$

他の関数との関係

シグモイド関数は、双曲線正接関数 ${\displaystyle \tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}$ を使って ${\displaystyle \varsigma _{a}(x)={\frac {\tanh(ax/2)+1}{2}}}$ とも表せる。またロジスティック関数 ${\displaystyle N={\frac {K}{1+\exp {rK(t_{0}-t)}}}}$において ${\displaystyle r=a,K=1,t_{0}=0}$ とした場合に当たる。

応用

導関数をシグモイド関数自身で簡単に導出できるため、微分成分が必要となるバックプロパゲーションに適している。ニューラルネットワークにおける活性化関数などで用いられる。

関連項目

• フェルミ分布関数
• ロジスティック関数

外部リンク

• 『シグモイド関数の意味と簡単な性質』 - 高校数学の美しい物語