エアリー関数 (エアリーかんすう、英 : Airy function 第一種エアリー関数 (Airy function of the first kind ) Ai(x ) イギリス の天文学者 ジョージ・ビドル・エアリー (1801–92) に因んで名づけられた特殊関数 である。この関数 Ai(x ) および第二種エアリー関数 とも呼ばれる関連の関数(A を次の文字 B に変えて、故に冗談めかしてベアリー (B iry) 関数とも)Bi(x ) エアリー方程式 あるいはストークス方程式 と呼ばれる微分方程式
d 2 y d x 2 − x y = 0 {\displaystyle {\frac {d^{2}y}{dx^{2}}}-xy=0} の線型独立な解としても言及される。これは転回点(turning point : 方程式の解が振動型から指数型へ変わる特徴点)を持つ最も単純な二階線型微分方程式 である。
エアリー関数は三角ポテンシャル井戸 に留め置かれた粒子に対する、あるいは一次元定力場における粒子に対するシュレーディンガー方程式 の解である。同じ理由により、ポテンシャルが位置の線型関数で局所近似されるときの、転回点の周りでのWKB近似 として、エアリー関数は一様半古典近似を与えるのに利用できる。三角ポテンシャル井戸解は、多くの半導体デバイスを理解することに直接的に関係がある。
エアリー関数はまた、虹 のような方向性集光(英語版) の周辺強度の形でも根底にある [訳語疑問点 。歴史的にはこれがエアリーがこの特殊関数を導入するに至った数学的問題であった。またエアリー関数は顕微鏡学(英語版) や天文学 においても重要である。つまり、エアリー関数は(顕微鏡 や望遠鏡 の解像限界よりも小さな)点光源(英語版) によって与えられる回折 や干渉のパターンを記述する。
定義 Ai(x ) を赤、Bi(x ) を青でプロット実 変数 x に対する第一種エアリー関数は広義リーマン積分
Ai ( x ) = 1 π ∫ 0 ∞ cos ( t 3 3 + x t ) d t ≡ 1 π lim b → ∞ ∫ 0 b cos ( t 3 3 + x t ) d t {\displaystyle {\begin{aligned}\operatorname {Ai} (x)&={\frac {1}{\pi }}\int _{0}^{\infty }\cos \left({\frac {t^{3}}{3}}+xt\right)~dt\\&\equiv {\frac {1}{\pi }}\lim _{b\to \infty }\int _{0}^{b}\cos \left({\frac {t^{3}}{3}}+xt\right)~dt\end{aligned}}} として定義することができる。これが収束することは、激しく振動するグラフの正の成分と負の成分とが互いに打ち消し合う (これは部分積分 で確認できる)ことによるものである。
関数 y = Ai(x )
y ″ − x y = 0 {\displaystyle y''-xy=0} を満足する。この方程式は二つの線型独立 な解を持つ。スカラー倍の違いを除いて 、Ai(x ) は x → ∞y → 0Bi(x ) を取るのが標準的である。第二種エアリー関数は第一種エアリー関数 Ai(x ) と同じ振幅を持ち x → −∞π/2 だけ異なる解
Bi ( x ) = 1 π ∫ 0 ∞ [ exp ( − t 3 3 + x t ) + sin ( t 3 3 + x t ) ] d t {\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\left[\exp \left(-{\frac {t^{3}}{3}}+xt\right)+\sin \left({\frac {t^{3}}{3}}+xt\right)\right]dt} として定義することができる。
性質 Ai(x ), Bi(x ) およびそれらの導関数の x = 0
Ai ( 0 ) = 1 3 2 / 3 Γ ( 2 / 3 ) , Ai ′ ( 0 ) = − 1 3 1 / 3 Γ ( 1 / 3 ) , Bi ( 0 ) = 1 3 1 / 6 Γ ( 2 / 3 ) , Bi ′ ( 0 ) = 3 1 / 6 Γ ( 1 / 3 ) {\displaystyle {\begin{aligned}\operatorname {Ai} (0)&={\frac {1}{3^{2/3}\Gamma (2/3)}},&\operatorname {Ai} '(0)&=-{\frac {1}{3^{1/3}\Gamma (1/3)}},\\\operatorname {Bi} (0)&={\frac {1}{3^{1/6}\Gamma (2/3)}},&\operatorname {Bi} '(0)&={\frac {3^{1/6}}{\Gamma (1/3)}}\end{aligned}}} で与えられる。ここで Γ はガンマ関数 である。これにより Ai(x ) および Bi(x ) のロンスキアン が 1/π となることが従う。
x が正のとき、Ai(x ) は正値凸関数 かつ指数関数的に零に減少し、Bi(x ) は正値凸関数かつ零の周辺で限りなく小さい振幅を以って無限回振動する。x が負のとき、Ai(x ), Bi(x ) はともに零の周辺で限りなく小さくなる振幅を以って無限回振動する。これはエアリー関数に対する漸近公式(後述 )によって保証される。
任意の変数に対するエアリー関数同士は、広義リーマン積分
∫ − ∞ ∞ Ai ( t + x ) Ai ( t + y ) d t = δ ( x − y ) {\displaystyle \int _{-\infty }^{\infty }\operatorname {Ai} (t+x)\operatorname {Ai} (t+y)\,{\mathit {dt}}=\delta (x-y)} が成り立つという意味において互いに直交する[1]
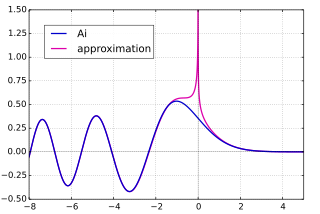
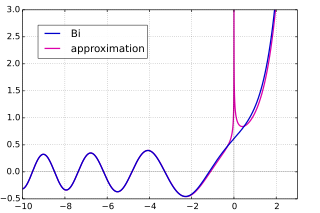
漸近公式 関数 Ai (青) とその正弦型/指数型漸近近似 (赤) 関数 Bi (青) とその正弦型/指数型漸近近似 (赤) 後述 のように、エアリー関数は複素数平面上へ延長することができて整関数 を与える。そのエアリー関数の偏角 arg(z ) が一定値を保ったまま |z | を無限大 へ飛ばすときの漸近挙動は arg(z ) に依存して決まる(これをストークス現象(英語版) と言う)。|arg(z )| < π のとき、Ai(z ) に対して以下の漸近公式
Ai ( z ) ∼ e − 2 3 z 3 2 2 π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] {\displaystyle \operatorname {Ai} (z)\sim {\dfrac {e^{-{\frac {2}{3}}z^{\frac {3}{2}}}}{2{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right]} を得る[2] Bi(z ) に対しても同様の漸近公式
Bi ( z ) ∼ e 2 3 z 3 2 π z 1 4 [ ∑ n = 0 ∞ Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] {\displaystyle \operatorname {Bi} (z)\sim {\frac {e^{{\frac {2}{3}}z^{\frac {3}{2}}}}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right]} 存在するが |arg(z )| < π/3 でしか適用できない。
π/3 < |arg(z )| < π のときのより正確な Ai(z ) および Bi(z ) に対する公式、あるいは同じことだが |arg(z )| < 2π/3 だが零でないときの Ai(−z ) および Bi(−z ) の漸近近似が
A i ( − z ) ∼ sin ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] − cos ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] B i ( − z ) ∼ cos ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] + sin ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] {\displaystyle {\begin{aligned}\mathrm {Ai} (-z)\sim &{}{\frac {\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}-{\frac {\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\\[6pt]\mathrm {Bi} (-z)\sim &{}{\frac {\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}+{\frac {\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\end{aligned}}} で与えられる[3]
|arg(z )| = 0 のとき、これらは良い近似であるが漸近的でない(Ai(−z ) または Bi(−z ) と上記の近似式との比は、現れる正弦および余弦の値が零となるところで無限大に発散することによる)。これらの極限に対する漸近展開も可能である。それらについては (Abramowitz & Stegun 1954 ) および (Olver 1974 ) にある。
複素エアリー関数 エアリー関数の定義を
Ai ( z ) = 1 2 π i ∫ C exp ( t 3 3 − z t ) d t {\displaystyle \operatorname {Ai} (z)={\frac {1}{2\pi i}}\int _{C}\exp \left({\frac {t^{3}}{3}}-zt\right)dt} と置くことにより複素数平面まで拡張することができる。ただし、積分路 C は偏角 −π /2 の無限遠点 −∞i から偏角 π /2∞i までとる。あるいは、微分方程式 y ′′ − xy = 0Ai(x ) および Bi(x ) を複素数平面上の整関数 に拡張することもできる。
Ai(x ) に対する漸近公式は、x 2/3 x が負の実軸の近くを除いて有界ならば、複素数平面上でもやはり有効である。Bi(x ) に対する漸近公式が有効なのは、x が適当な δ > 0 に対する扇形 {x ∈ C : |arg(x )| < π 3 にあるときである。また、Ai(−x ), Bi(−x ) に対する公式は x が扇形 {x ∈ C : |arg(x )| < 2π ⁄3 にあるとき有効である。
エアリー関数の漸近的挙動から分かることは、Ai(x ), Bi(x ) ともに負の実軸上に無限個の零点を持つことである。関数 Ai(x ) は複素数平面上に他の零点を持たないが、Bi(x ) は扇形 {z ∈ C : π 3 z )| < π 2 にも無限個の零点を持つ。
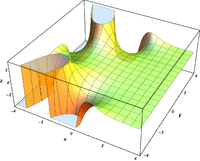
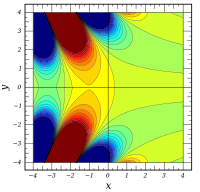
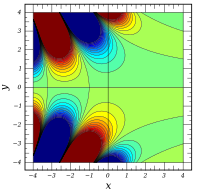
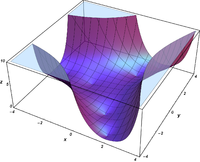
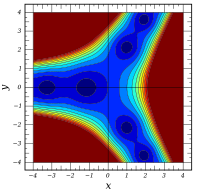
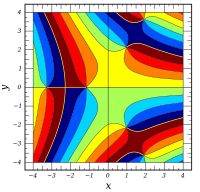
グラフ ℜ [ Ai ( x + i y ) ] {\displaystyle \Re [\operatorname {Ai} (x+iy)]} ℑ [ Ai ( x + i y ) ] {\displaystyle \Im [\operatorname {Ai} (x+iy)]} | Ai ( x + i y ) | {\displaystyle |\operatorname {Ai} (x+iy)|} arg [ Ai ( x + i y ) ] {\displaystyle \operatorname {arg} [\operatorname {Ai} (x+iy)]}
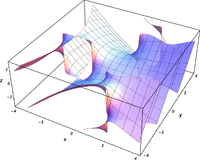
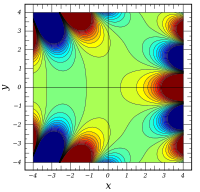
ℜ [ Bi ( x + i y ) ] {\displaystyle \Re [\operatorname {Bi} (x+iy)]} ℑ [ Bi ( x + i y ) ] {\displaystyle \Im [\operatorname {Bi} (x+iy)]} | Bi ( x + i y ) | {\displaystyle |\operatorname {Bi} (x+iy)|} arg [ Bi ( x + i y ) ] {\displaystyle \operatorname {arg} [\operatorname {Bi} (x+iy)]}
他の特殊関数との関係 正の引数に対して、エアリー関数は変形ベッセル関数 と
Ai ( x ) = 1 π x 3 K 1 / 3 ( 2 x 3 / 2 / 3 ) , Bi ( x ) = x 3 ( I 1 / 3 ( 2 x 3 / 2 / 3 ) + I − 1 / 3 ( 2 x 3 / 2 / 3 ) ) {\displaystyle {\begin{aligned}\operatorname {Ai} (x)&={\frac {1}{\pi }}{\sqrt {\frac {x}{3}}}\,K_{1/3}(2x^{3/2}/3),\\[8pt]\operatorname {Bi} (x)&={\sqrt {\frac {x}{3}}}\left(I_{1/3}(2x^{3/2}/3)+I_{-1/3}(2x^{3/2}/3)\right)\end{aligned}}} なる関係を持つ。ここで I ±1/3 , K 1/3 x 2 y" + xy' − (x 2 + 1 ⁄9 y = 0
Ai ′ ( x ) = − x π 3 K 2 / 3 ( 2 x 3 / 2 / 3 ) {\displaystyle \operatorname {Ai} '(x)=-{\frac {x}{\pi {\sqrt {3}}}}\,K_{2/3}(2x^{3/2}/3)} であり、関数 K 1/3 K 2/3 [4] 変形ベッセル関数 の項も参照)。
負の引数に対して、エアリー関数はベッセル関数 と
Ai ( − x ) = x 9 ( J 1 / 3 ( 2 x 3 / 2 / 3 ) + J − 1 / 3 ( 2 x 3 / 2 / 3 ) ) , Bi ( − x ) = x 3 ( J − 1 / 3 ( 2 x 3 / 2 / 3 ) − J 1 / 3 ( 2 x 3 / 2 / 3 ) ) {\displaystyle {\begin{aligned}\operatorname {Ai} (-x)&={\sqrt {\frac {x}{9}}}\left(J_{1/3}(2x^{3/2}/3)+J_{-1/3}(2x^{3/2}/3)\right),\\[8pt]\operatorname {Bi} (-x)&={\sqrt {\frac {x}{3}}}\left(J_{-1/3}(2x^{3/2}/3)-J_{1/3}(2x^{3/2}/3)\right)\end{aligned}}} なる関係を持つ。ここに J ±1/3 x 2 y" + xy' + (x 2 − 1 ⁄9 y = 0
スコアラーの関数(英語版) (y" − xy = 1/π
Gi ( x ) = Bi ( x ) ∫ x ∞ Ai ( t ) d t + Ai ( x ) ∫ 0 x Bi ( t ) d t , Hi ( x ) = Bi ( x ) ∫ − ∞ x Ai ( t ) d t − Ai ( x ) ∫ − ∞ x Bi ( t ) d t {\displaystyle {\begin{aligned}\operatorname {Gi} (x)&=\operatorname {Bi} (x)\int _{x}^{\infty }\operatorname {Ai} (t){\mathit {dt}}+\operatorname {Ai} (x)\int _{0}^{x}\operatorname {Bi} (t){\mathit {dt}},\\[8pt]\operatorname {Hi} (x)&=\operatorname {Bi} (x)\int _{-\infty }^{x}\operatorname {Ai} (t){\mathit {dt}}-\operatorname {Ai} (x)\int _{-\infty }^{x}\operatorname {Bi} (t){\mathit {dt}}\end{aligned}}} と書くこともできる。
フーリエ変換 エアリー関数 Ai(x ) の定義から直接に、そのフーリエ変換 が
F ( Ai ) ( k ) := ∫ − ∞ ∞ Ai ( x ) e − 2 π i k x d x = e i ( 2 π k ) 3 / 3 {\displaystyle {\mathcal {F}}(\operatorname {Ai} )(k):=\int _{-\infty }^{\infty }\operatorname {Ai} (x)\ e^{-2\pi ikx}\,dx=e^{i(2\pi k)^{3}/3}} で与えられることが示せる。
歴史 エアリー関数の名の由来は、イギリス人 天文学者 ・物理学者 のジョージ・ビドル・エアリー (1801–1892) である。エアリーは光学 の初期研究 (Airy 1838) においてこの関数に遭遇した。"Ai(x ) " という表記はハロルド・ジェフリースによるものである。エアリーはイギリス王室天文官 を1835年から1881年まで務めた人物である。
関連項目 出典 [脚注の使い方 ]
^ David E. Aspnes, Physical Review, 147 , 554 (1966) ^ Abramowitz & Stegun 1970 , p. 448, Eqns 10.4.59 and 10.4.63^ Abramowitz & Stegun 1970 , p. 448, Eqns 10.4.60 and 10.4.64^ M.Kh.Khokonov. Cascade Processes of Energy Loss by Emission of Hard Photons // JETP, V.99, No.4, pp. 690-707 \ (2004). 注釈 [脚注の使い方 ]
参考文献 Abramowitz, Milton [in 英語] ; Stegun, Irene Ann [in 英語] , eds. (1983) [June 1964]. "Chapter 10". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables . Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 446. ISBN 978-0-486-61272-0 . LCCN 64-60036. MR 0167642. LCCN 65-12253。 Airy (1838), “On the intensity of light in the neighbourhood of a caustic”, Transactions of the Cambridge Philosophical Society (University Press) 6 : 379–402, https://books.google.co.jp/books?id=-yI8AAAAMAAJ&dq=Transactions+of+the+Cambridge+Philosophical+Society+1838&redir_esc=y&hl=ja Frank William John Olver (1974). Asymptotics and Special Functions, Chapter 11. Academic Press, New York. Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), “Section 6.6.3. Airy Functions”, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=289 Vallée, Olivier; Soares, Manuel (2004), Airy functions and applications to physics , London: Imperial College Press, ISBN 978-1-86094-478-9, MR 2114198, http://www.worldscibooks.com/physics/p345.html 外部リンク Hazewinkel, Michiel, ed. (2001), “Airy functions”, Encyclopedia of Mathematics , Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Airy_functions Weisstein, Eric W. "Airy Functions". mathworld.wolfram.com (英語). Wolfram function pages for Ai and Bi functions. Includes formulas, function evaluator, and plotting calculator. Olver, F. W. J. (2010), “Airy and related functions”, in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions ISBN 978-0521192255, http://dlmf.nist.gov/9 典拠管理データベース
全般 国立図書館 フランス BnF data ドイツ イスラエル アメリカ その他












![{\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\left[\exp \left(-{\frac {t^{3}}{3}}+xt\right)+\sin \left({\frac {t^{3}}{3}}+xt\right)\right]dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8643d2f933f27a7a48c0b71678feb0f5380d192e)


![{\displaystyle \operatorname {Ai} (z)\sim {\dfrac {e^{-{\frac {2}{3}}z^{\frac {3}{2}}}}{2{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/806ad23ede95fa953103bdb93158b10e31f99ff7)
![{\displaystyle \operatorname {Bi} (z)\sim {\frac {e^{{\frac {2}{3}}z^{\frac {3}{2}}}}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ed0222eb216d9ca047f43205177f86a9cf0ddd1)
![{\displaystyle {\begin{aligned}\mathrm {Ai} (-z)\sim &{}{\frac {\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}-{\frac {\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\\[6pt]\mathrm {Bi} (-z)\sim &{}{\frac {\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}+{\frac {\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78b18b75027eac854d45c9facb56b05e2319f04d)

![{\displaystyle \Re [\operatorname {Ai} (x+iy)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639332bc4bfac511cf4494e7da82b66e38093bc2)
![{\displaystyle \Im [\operatorname {Ai} (x+iy)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf75f231805495fd78d859da17c681b5c1286d6d)

![{\displaystyle \operatorname {arg} [\operatorname {Ai} (x+iy)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4611792b12dbf127a110f7bb142a6961b36acde)
![{\displaystyle \Re [\operatorname {Bi} (x+iy)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/852f66b2adad5421e7fc4c01a2786ca1e1ae27da)
![{\displaystyle \Im [\operatorname {Bi} (x+iy)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cb51eb4e94c5caa70e055375cf4edd3e2f7e7de)

![{\displaystyle \operatorname {arg} [\operatorname {Bi} (x+iy)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/badae6ccdc570b89243edf483f6e0aec9de137ff)
![{\displaystyle {\begin{aligned}\operatorname {Ai} (x)&={\frac {1}{\pi }}{\sqrt {\frac {x}{3}}}\,K_{1/3}(2x^{3/2}/3),\\[8pt]\operatorname {Bi} (x)&={\sqrt {\frac {x}{3}}}\left(I_{1/3}(2x^{3/2}/3)+I_{-1/3}(2x^{3/2}/3)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e14d5ee82a89db672452944a2a014fb31dec99bc)

![{\displaystyle {\begin{aligned}\operatorname {Ai} (-x)&={\sqrt {\frac {x}{9}}}\left(J_{1/3}(2x^{3/2}/3)+J_{-1/3}(2x^{3/2}/3)\right),\\[8pt]\operatorname {Bi} (-x)&={\sqrt {\frac {x}{3}}}\left(J_{-1/3}(2x^{3/2}/3)-J_{1/3}(2x^{3/2}/3)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5eed5ee29d5aa0c12de2070da274a751c37c043)
![{\displaystyle {\begin{aligned}\operatorname {Gi} (x)&=\operatorname {Bi} (x)\int _{x}^{\infty }\operatorname {Ai} (t){\mathit {dt}}+\operatorname {Ai} (x)\int _{0}^{x}\operatorname {Bi} (t){\mathit {dt}},\\[8pt]\operatorname {Hi} (x)&=\operatorname {Bi} (x)\int _{-\infty }^{x}\operatorname {Ai} (t){\mathit {dt}}-\operatorname {Ai} (x)\int _{-\infty }^{x}\operatorname {Bi} (t){\mathit {dt}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8bc9f4b6ba407b3806c3eba45eedcea463a9759)







