Omologia singolare

In topologia l'omologia singolare è una costruzione che permette di associare ad uno spazio topologico un oggetto algebrico detto omologia.

Esistono altre costruzioni che producono essenzialmente la stessa omologia, ad esempio l'omologia simpliciale e l'omologia cellulare. L'omologia singolare è la costruzione che funziona nella più ampia generalità: per la sua costruzione non è necessario che lo spazio topologico sia un complesso simpliciale o un complesso di celle.

Definizione

Sia ${\displaystyle X}$ uno spazio topologico. Come ogni omologia, l'omologia singolare è definita a partire da un complesso di catene

${\displaystyle \dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\partial _{0}}{\longrightarrow \,}}0.}$

Il complesso di catene qui è costruito a partire dalla nozione di simplesso singolare.

Simplesso standard

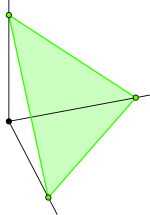
Il simplesso standard ${\displaystyle \Delta _{n}}$ è l'inviluppo convesso in ${\displaystyle \mathbb {R} ^{n+1}}$ dei punti

${\displaystyle e_{0},\ldots ,e_{n}}$

che formano la base canonica di ${\displaystyle \mathbb {R} ^{n+1}}$. Per ${\displaystyle n=1,2,3}$ il simplesso standard è rispettivamente un segmento, un triangolo, un tetraedro. I punti ${\displaystyle e_{0},e_{1},\ldots ,e_{n}}$ sono i vertici del simplesso. Il simplesso ${\displaystyle \Delta _{n}}$ ha dimensione ${\displaystyle n}$.

Una faccia di dimensione ${\displaystyle k}$ di ${\displaystyle \Delta _{n}}$ è l'inviluppo convesso di ${\displaystyle k+1}$ vertici distinti

${\displaystyle e_{i_{0}},\ldots ,e_{i_{k}}.}$

Tale faccia è canonicamente identificata con il simplesso standard ${\displaystyle \Delta _{k}}$: il fatto che questa identificazione sia canonica è un punto essenziale della teoria, che dipende dal fatto che i vertici del simplesso standard sono ordinati. Se ${\displaystyle i_{0}<\ldots <i_{k}}$, l'identificazione ${\displaystyle F}$ è tale che

${\displaystyle F(e_{i_{j}})=e_{j}}$

e si estende per combinazione convessa a tutta la faccia.

Se la dimensione non è specificata, per faccia di ${\displaystyle \Delta _{n}}$ si intende una faccia di dimensione ${\displaystyle n-1}$: queste giocano un ruolo importante nella costruzione dell'omologia singolare. Il simplesso ${\displaystyle \Delta _{n}}$ ha quindi ${\displaystyle n+1}$ facce ${\displaystyle f_{0},\ldots ,f_{n}}$ opposte ai vertici ${\displaystyle e_{0},\ldots ,e_{n}}$.

Simplesso singolare

Sia ${\displaystyle X}$ uno spazio topologico Un simplesso singolare è una mappa continua

${\displaystyle \sigma \colon \Delta _{n}\to X}$

dal simplesso standard in ${\displaystyle X}$. Anche qui ${\displaystyle n}$ è la dimensione del simplesso singolare. Il bordo ${\displaystyle i}$-esimo ${\displaystyle \partial _{i}\sigma }$ del simplesso singolare ${\displaystyle \sigma }$ è il simplesso singolare di dimensione ${\displaystyle n-1}$ seguente:

${\displaystyle \partial _{i}\sigma \colon \Delta _{n-1}\to X}$

definito restringendo ${\displaystyle \sigma }$ alla ${\displaystyle i}$-esima faccia di ${\displaystyle \Delta _{n}}$ (identificata canonicamente con ${\displaystyle \Delta _{n-1}}$).

Complesso di catene

Una catena è una combinazione lineare formale di simplessi singolari (tutti della stessa dimensione ${\displaystyle n}$), a coefficienti interi

${\displaystyle a_{1}\sigma _{1}+\ldots +a_{h}\sigma _{h}.}$

Il numero ${\displaystyle h}$ di elementi è variabile (purché finito) e i coefficienti ${\displaystyle a_{i}}$ sono numeri interi. Una catena non è una mappa: può essere interpretata solo astrattamente, come combinazione lineare formale di oggetti. Le catene possono essere sommate in modo naturale e formano un gruppo abeliano, indicato con ${\displaystyle C_{n}}$. In altre parole, ${\displaystyle C_{n}}$ è il gruppo abeliano libero generato dall'insieme di tutti i simplessi singolari. Questo insieme è in generale molto grande (può avere cardinalità più che numerabile anche per spazi ${\displaystyle X}$ molto semplici).

Per definire un complesso di catene è infine necessario introdurre una mappa di bordo

${\displaystyle \partial \colon C_{n}\to C_{n-1}.}$

per ogni ${\displaystyle n>0}$. La mappa è definita su ogni simplesso singolare ${\displaystyle \sigma }$ di dimensione ${\displaystyle n}$ nel modo seguente:

${\displaystyle \partial \sigma =\sum _{i=0}^{n}(-1)^{i}\partial _{i}\sigma .}$

La mappa ${\displaystyle \partial }$ è quindi estesa per linearità a tutto ${\displaystyle C_{n}}$.

Omologia

La costruzione descritta produce finalmente un complesso di catene

${\displaystyle \dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\partial _{0}}{\longrightarrow \,}}0.}$

L'alternanza dei segni nella definizione di ${\displaystyle \partial }$ ha un importante effetto: la composizione di due bordi successivi è sempre la mappa banale, cioè quella che manda ogni simplesso nello zero (lo zero in ${\displaystyle C_{n}}$ è la combinazione lineare vuota). Infatti facendo due volte il bordo di un ${\displaystyle n}$-simplesso singolare si ottiene una catena in cui ogni ${\displaystyle (n-2)}$-sottosimplesso singolare compare due volte, ma con segni opposti. Vale quindi la proprietà

${\displaystyle \partial _{n}\circ \partial _{n+1}=0.}$

A questo punto l'omologia singolare è definita a partire da questo complesso con un procedimento standard, usato in tutte le teorie omologiche. Si definisce l'${\displaystyle n}$-esimo gruppo di omologia singolare ${\displaystyle H_{n}(X)}$ come il gruppo quoziente

${\displaystyle H_{n}(X)=\ker(\partial _{n})/\mathrm {im} (\partial _{n+1}).}$

Bibliografia

• (EN) Allen Hatcher, Algebraic topology. Cambridge University Press, ISBN 0-521-79160-X and ISBN 0-521-79540-0
• (EN) J.P. May, A Concise Course in Algebraic Topology, Chicago University Press ISBN 0-226-51183-9
• (EN) Joseph J. Rotman, An Introduction to Algebraic Topology, Springer-Verlag, ISBN 0-387-96678-1