Funzione a supporto compatto

In matematica, una funzione a valori reali o complessi definita su un dominio di ${\displaystyle \mathbb {R} ^{n}}$ (o, più in generale, in uno spazio topologico) si dice funzione a supporto compatto se ha per supporto un sottoinsieme compatto dell'insieme di definizione (il supporto è definito come la chiusura dell'insieme dei punti del dominio in cui la funzione non si annulla).

Rivestono particolare importanza le funzioni a supporto compatto che sono anche continue o infinitamente differenziabili: in tal caso si restringe il campo ad una classe molto ristretta di funzioni, dette funzioni di test, che vengono usate principalmente nella teoria delle distribuzioni.

Dal teorema di Heine-Borel e dalla definizione di supporto di una funzione segue che una funzione è a supporto compatto se è diversa da 0 in un insieme chiuso e limitato di punti.

Definizione

Una funzione definita su uno spazio topologico ${\displaystyle X}$ si dice essere a supporto compatto se il suo supporto:

${\displaystyle \mathrm {supp} \,f:={\overline {\{\mathbf {x} \in X:f(\mathbf {x} )\neq \mathbf {0} \}}}}$

è un sottoinsieme compatto di ${\displaystyle X}$, ovvero per ogni famiglia ${\displaystyle \{U_{i}\}_{i\in I}}$ di sottoinsiemi aperti di ${\displaystyle \mathrm {supp} \,f}$ tale che:

${\displaystyle \bigcup _{i\in I}U_{i}\supseteq \mathrm {supp} \,f}$

esiste un sottoinsieme finito ${\displaystyle J}$ di ${\displaystyle I}$ tale che:^[1]

${\displaystyle \bigcup _{i\in J}U_{i}\supseteq \mathrm {supp} \,f}$

Un'importante classe di funzioni a supporto compatto è quella delle funzioni test. Lo spazio delle funzioni test sul dominio ${\displaystyle O}$ di ${\displaystyle \mathbb {R} ^{n}}$ è chiamato ${\displaystyle D(O)}$, mentre lo spazio delle funzioni test su ${\displaystyle \mathbb {R} ^{n}}$ è denotato con ${\displaystyle D}$, ove non sia necessario specificare il numero di variabili.

È da notare che una funzione a supporto compatto in un dato dominio di ${\displaystyle \mathbb {R} ^{n}}$ può essere prolungata in modo naturale ad una funzione a supporto compatto su tutto ${\displaystyle \mathbb {R} ^{n}}$ semplicemente assegnando il valore 0 a tutti i punti al di fuori del dominio originario. In questo modo è possibile pensare ad una funzione in ${\displaystyle D(O)}$ come avente dominio in ${\displaystyle \mathbb {R} ^{n}}$, e quindi se ${\displaystyle O\subset O'\subset \mathbb {R} ^{n}}$ si ha anche ${\displaystyle D(O)\subset D(O')\subset D}$.

Le funzioni continue a supporto compatto

Una classe particolarmente importante di funzioni a supporto compatto è quella delle funzioni che sono anche continue. Si dimostra che lo spazio ${\displaystyle C_{c}(X)}$ delle funzioni continue a supporto compatto su uno spazio di Hausdorff localmente compatto ${\displaystyle X}$ e a valori complessi è denso in uno spazio L^p definito su uno spazio di misura, a patto che ${\displaystyle 1\leq p<\infty }$.^[2] Tale classe di funzioni gode inoltre della proprietà che due funzioni in ${\displaystyle C_{c}(\mathbb {R} ^{k})}$ differiscono soltanto per insiemi di misura di Lebesgue non nulla, e pertanto se sono uguali quasi ovunque allora sono uguali. Inoltre, facendo coincidere ${\displaystyle X}$ con lo spazio ${\displaystyle \mathbb {R} ^{k}}$, poiché ${\displaystyle L^{p}(\mathbb {R} ^{k})}$ è completo, esso è il completamento dello spazio ottenuto dotando ${\displaystyle C_{c}(\mathbb {R} ^{k})}$ della ${\displaystyle L^{p}}$-metrica. Nel caso in cui ${\displaystyle p=\infty }$, il completamento di ${\displaystyle C_{c}(\mathbb {R} ^{k})}$ tramite la ${\displaystyle L^{\infty }}$-metrica è lo spazio ${\displaystyle C_{0}(\mathbb {R} ^{k})}$ delle funzioni continue che si annullano all'infinito.^[3]

Proprietà

Le funzioni a supporto compatto godono inoltre delle seguenti proprietà.

• Data una funzione ${\displaystyle f}$ localmente integrabile in ${\displaystyle \mathbb {R} ^{n}}$ e una ${\displaystyle \phi }$ in ${\displaystyle D}$, allora l'integrale di Lebesgue:

${\displaystyle \int f(x)\phi (x)d^{n}x}$

ha sempre valore finito.

• Se ${\displaystyle g}$ è una funzione assolutamente continua su ${\displaystyle \mathbb {R} }$ con derivata di Radon-Nikodym ${\displaystyle g'}$, allora vale:

${\displaystyle \int g'(x)\phi (x)dx=-\int g(x)\phi '(x)dx}$

In altre parole, nell'eseguire l'integrazione per parti con una funzione test, i termini di bordo si annullano.

• La somma o il prodotto di due funzioni a supporto compatto è ancora a supporto compatto.

Convergenza

Lo spazio ${\displaystyle D(O)}$ può essere munito di una struttura di spazio topologico definendo un criterio di convergenza per le successioni. Una successione di funzioni ${\displaystyle \{\phi _{k}\}}$ di ${\displaystyle D(O)}$ converge a una funzione ${\displaystyle \phi \in D(O)}$ se il supporto di ${\displaystyle \phi _{k}}$ è contenuto nel supporto di ${\displaystyle \phi }$, e se le derivate di ogni ordine di ${\displaystyle \phi _{k}}$ convergono uniformemente alle corrispondenti derivate di ${\displaystyle \phi }$.

Si tratta di una condizione molto forte di convergenza. Infatti, una successione convergente in ${\displaystyle D(O)}$ è anche puntualmente convergente, uniformemente convergente e convergente nello spazio delle funzioni p-sommabili per ogni ${\displaystyle p}$.

Esempi

• Un esempio di funzione a supporto compatto è la funzione a campana:

${\displaystyle \Omega (x)={\begin{cases}e^{-{\frac {1}{1-|x|^{2}}}}&|x|<1\\0&|x|\geq 1\end{cases}}}$

definita su tutto ${\displaystyle \mathbb {R} ^{n}}$.

La funzione ${\displaystyle \operatorname {\Omega } }$ ha supporto nel disco chiuso di raggio 1 centrato nello 0, è infinitamente derivabile e si annulla con tutte le sue derivate per ${\displaystyle ||x||\to 1}$.

• Una stretta parente della funzione a campana è data, ${\displaystyle \forall \varepsilon >0}$, da:

${\displaystyle \Omega _{\varepsilon }(x)={\begin{cases}K_{\varepsilon }e^{-{\frac {1}{1-{\frac {|x|^{2}}{\varepsilon ^{2}}}}}}&|x|<\varepsilon \\0&|x|\geq \varepsilon \end{cases}}}$

dove ${\displaystyle K_{\varepsilon }}$ è una costante reale positiva scelta in modo da avere:

${\displaystyle \int \Omega _{\varepsilon }(x)d^{n}x=1}$

La funzione ${\displaystyle \operatorname {\Omega _{\varepsilon }} }$ gode delle stesse proprietà della campana, salvo che ha supporto nel disco chiuso di raggio ${\displaystyle \varepsilon }$. Si può dimostrare che le ${\displaystyle \operatorname {\Omega _{\varepsilon }} }$ sono approssimanti della delta, nel senso che, presa una funzione ${\displaystyle \operatorname {\phi } }$ continua nello 0, vale ${\displaystyle \lim _{\varepsilon \to 0}\,\int \Omega _{\varepsilon }(x)\phi (x)d^{n}x=\phi (0)}$.

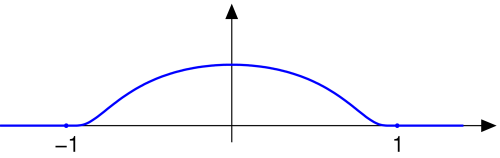
• Un'importante funzione a supporto compatto in una variabile si ottiene dalla convoluzione di ${\displaystyle \operatorname {\Omega _{\varepsilon }} }$ con la funzione caratteristica ${\displaystyle \operatorname {\chi } _{[-1,1]}(x)}$, che vale 1 per ${\displaystyle -1\leq x\leq 1}$ e 0 altrimenti. Si ha quindi, per ogni ${\displaystyle \varepsilon >0}$:

${\displaystyle \operatorname {\chi _{\varepsilon }(x)} =\int \Omega _{\varepsilon }(x-y)\chi _{[-1,1]}(y)dy}$

Si vede che, per questa funzione, vale:

${\displaystyle \chi _{\varepsilon }(x)={\begin{cases}1&|x|<1-\varepsilon \\0&|x|>1+\varepsilon \end{cases}}}$

quindi, per ${\displaystyle \varepsilon \to 0,\operatorname {\chi _{\varepsilon }(x)} \to \operatorname {\chi } _{[-1,1]}(x)}$ puntualmente.

Note

Bibliografia

• (EN) Walter Rudin, Real and Complex Analysis, Mladinska Knjiga, McGraw-Hill, 1970, ISBN 0-07-054234-1.
  • trad. it.: Analisi reale e complessa, Trad. Maria Laura Vesentini - Edoardo Vesentini, coll. Programma di matematica fisica elettronica, Torino, Boringhieri, 1974, ISBN 978-88-339-5342-7.
• (EN) K. Yosida, Functional analysis , Springer (1980) pp. Chapt. 8, Sect. 4; 5

Voci correlate

• Funzione continua
• Funzione liscia
• Funzione test
• Funzione di cutoff
• Spazio compatto
• Supporto (matematica)
• Teorema di Heine-Borel

Collegamenti esterni

• (EN) Funzione a supporto compatto, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica