Curva quartica

In matematica una curva quartica è una curva algebrica piana di quarto grado. Può essere definita da un polinomio della forma:

${\displaystyle Ax^{4}+Bx^{3}y+Cx^{2}y^{2}+Dxy^{3}+Ey^{4}+Fx^{3}+Gx^{2}y+Hxy^{2}+Iy^{3}+Jx^{2}+Kxy+Ly^{2}+Mx+Ny+O=0.}$

Una curva quartica (${\displaystyle n=4}$) irriducibile può avere al massimo:

${\displaystyle {\frac {1}{2}}(n-1)(n-2)+1=4}$ componenti connesse;

${\displaystyle {\frac {1}{2}}(n-1)(n-2)=3}$ punti doppi;

${\displaystyle {\frac {n}{2}}(n-2)(n^{2}-9)=28}$ rette bitangenti;

${\displaystyle 3n(n-2)=24}$ punti di flesso.

L'equazione ha 15 coefficienti, ma la curva non cambia se li moltiplichiamo tutti per una costante non nulla. Quindi i coefficienti essenziali sono 14 e le quartiche sono ${\displaystyle \infty ^{14}}$. E una di esse è individuata dal suo passaggio per 14 punti generici.

Esempi

• Curva a bicorno o a feluca

${\displaystyle y^{2}(a^{2}-x^{2})-(x^{2}+2ay-a^{2})^{2}=0}$

• Curva a kappa o di Gutschoven

${\displaystyle y^{2}(x^{2}+y^{2})-a^{2}x^{2}=0}$

• Curva a sabbia cadente

${\displaystyle x^{2}y^{2}-a^{2}y^{2}+1=0}$

• Pallottole punta a punta

${\displaystyle a^{2}y^{2}-b^{2}x^{2}-x^{2}y^{2}=0}$

• Trisettrice di Delange

${\displaystyle y^{2}(x^{2}+y^{2})-4a^{2}(x^{2}+y^{2}-1)=0}$

• Curva di Edge quadriconnessa

${\displaystyle 25(x^{4}+y^{4}+1)-34(x^{2}y^{2}+x^{2}+y^{2})=0}$

• Curva a uovo storto

${\displaystyle x^{4}+y^{4}+2x^{2}y^{2}-x^{3}-y^{3}=0}$

• Curva a uovo dritto

${\displaystyle 5x^{4}+y^{4}+10x^{2}y^{2}-y=0}$

• Uovo di Keplero

${\displaystyle (x^{2}+y^{2})^{2}-ax^{3}=0}$

• Curva a uovo doppio

${\displaystyle [y^{2}(1-2a)-x^{2}+a^{2}b^{2}-1]^{2}+4x^{2}[y^{2}(1-b)^{2}-1]=0}$

• Curva di Granville

${\displaystyle x^{2}y^{2}+(x-a)(x-1)=0}$

• Curva di Helton-Vinnikov

${\displaystyle 2x^{4}+y^{4}+1-3x^{2}y^{2}-3x^{2}+y^{2}=0}$

• Curva di Klein

${\displaystyle x^{3}y+ay^{3}+a^{3}x=0}$

• Curva a fagiolo o a pisello

${\displaystyle x^{4}+y^{4}+x^{2}y^{2}-x(x^{2}+y^{2})=0}$

• Superellisse o Curva di Lamè

${\displaystyle x^{4}/a^{4}+y^{4}/b^{4}-c^{4}=0}$

• Supercerchio

${\displaystyle x^{4}+y^{4}-c^{4}=0}$

• Curva a fiocco

${\displaystyle x^{4}+y^{3}-x^{2}y=0}$

• Curva intrecciata

${\displaystyle (x^{2}+y^{2})^{2}-2x^{3}-6y^{2}x+x^{2}=0}$

• Curva a nodo

${\displaystyle (x^{2}-1)^{2}-y^{2}(2y+3)=0}$

• Campila di Eudosso

${\displaystyle x^{4}-x^{2}-y^{2}=0}$

• Curva Cardioide

${\displaystyle (x^{2}+y^{2}-x)^{2}-x^{2}-y^{2}=0}$

• Curva Ampersand trinodata

${\displaystyle (y^{2}-x^{2})(x-1)(2x-3)-4(x^{2}+y^{2}-2x)^{2}=0}$

• Curva di Jerabek

${\displaystyle (x^{2}+y^{2})(x-1)^{2}-4(x^{2}+y^{2}-x)^{2}=0}$

• Curva a svastica

${\displaystyle x^{4}-y^{4}-xy=0}$

• Curva di Jubel

${\displaystyle (x^{2}-y^{2})^{2}-a^{2}x^{2}-b^{2}y^{2}=0}$

• Ovale di Mandelbrot

${\displaystyle (x^{2}+y^{2}+x)^{2}+y^{2}-4=0}$

• Curva bicuspidata

${\displaystyle (x^{2}-1)(x-1)^{2}+(y^{2}-1)^{2}=0}$

• Curva deltoide tricuspidata o di Steiner

${\displaystyle (x^{2}+y^{2})^{2}+18a^{2}(x^{2}+y^{2})-8a(x^{3}-3xy^{2})-27a^{4}=0}$

• Lemniscata di Bernoulli

${\displaystyle (x^{2}+y^{2})^{2}-a(x^{2}-y^{2})=0}$

• Lemniscata di Gerono o Curva a otto

${\displaystyle x^{4}-a(x^{2}-y^{2})=0}$

• Lemniscata di Booth o Ippopede di Proclo

${\displaystyle (x^{2}+y^{2})^{2}-ax^{2}-by^{2}=0}$

• Curva di Wassenaar

${\displaystyle (x^{2}-y)^{2}+ax^{2}-1=0}$

• Curva Multiovale

${\displaystyle a(x^{4}+y^{4})+by^{3}+cx^{2}y+dx^{2}+ey^{2}+f=0}$

• Lumaca di Pascal o di Durer o Concoide del cerchio

${\displaystyle (x^{2}+y^{2}-ax)^{2}-b^{2}(x^{2}+y^{2})=0}$

• Curva piriforme o a goccia d'acqua

${\displaystyle (x^{2}+y^{2})^{2}-a(x^{2}-y^{2})=0}$

• Curve bifogliate

${\displaystyle x^{4}+y^{4}+cx^{2}y^{2}+dxy^{2}=0}$

• Curve trifogliate

${\displaystyle x^{4}+y^{4}+dx^{2}y^{2}+exy^{2}+fx^{3}=0}$

• Curva del diavolo

${\displaystyle x^{4}-y^{4}+a^{2}y^{2}-b^{2}x^{2}=0}$

• Motore elettrico

${\displaystyle x^{2}(x^{2}-100)-y^{2}(y^{2}-96)=0}$

• Curva Capricornoide

${\displaystyle a^{2}x^{2}(x^{2}+y^{2})-b(ay-x^{2}-y^{2})^{2}=0}$

• Perle di Sluze

${\displaystyle y^{L}-a(b-x)^{M}x^{N}=0}$

ove ${\displaystyle L}$ e ${\displaystyle M+N}$ sono interi non superiori a 4

• Curva di Plucker

${\displaystyle (x^{2}-a^{2})^{2}+(y^{2}-a^{2})^{2}-b^{2}=0}$

• Curva a pesce

${\displaystyle (x^{2}-y^{2}+a^{2}-ab)^{2}-(a^{2}-y^{2})(2x+b)^{2}=0}$

• Concoide di Durer

${\displaystyle y^{2}-yx-ay-b^{2})^{2}+(y^{2}-b^{2})(a-y-x)^{2}=0}$

• Concoide di Kulp

${\displaystyle x^{2}y^{2}+a^{2}y^{2}-b^{2}=0}$

• Concoide di Nicomede

${\displaystyle (x-a)^{2}(x^{2}+y^{2})-b^{2}x^{2}=0}$

• Curva cruciforme

${\displaystyle x^{2}y^{2}-a^{2}(x^{2}+y^{2})=0}$

• Sezione spirica o di Perseo

${\displaystyle (x^{2}+y^{2})^{2}+dx^{2}+ey^{2}+f=0}$

• Sezione torica

${\displaystyle (x^{2}+y^{2})^{2}+ax^{2}+by^{2}+cx+dy+e=0}$

• Ovali di Cartesio

${\displaystyle [(1-a^{2})(x^{2}+y^{2})+2a^{2}bx+c^{2}-a^{2}b^{2}]^{2}-4c^{2}(x^{2}+y^{2})=0}$

• Ovali di Cassini

${\displaystyle (x^{2}+y^{2}+a^{2})^{2}-4a^{2}x^{2}-b^{4}=0}$

• Curve di Jacobi

${\displaystyle y^{2}=ax^{4}-2bx^{2}+1}$

• Curve di Edwards

${\displaystyle x^{2}+y^{2}=a(1-bx^{2}y^{2})}$

• Curve di Edwards ritorte

${\displaystyle ax^{2}y^{2}=bx^{2}+y^{2}-1}$

• Curva di Trott a 28 bitangenti

${\displaystyle 144(x^{4}+y^{4})-225(x^{2}+y^{2})+350x^{2}y^{2}+81=0}$

• Curva a 8 flessi

${\displaystyle x^{4}+y^{4}-x^{2}y^{2}-x^{2}-y^{2}=0}$

• Pedali del cerchio

${\displaystyle a^{2}[(u-x)^{2}+(v-y)^{2}]-(x^{2}+y^{2}-ux-vy)^{2}=0}$

ove il cerchio è ${\displaystyle x^{2}+y^{2}=a^{2}}$ e il punto pedale è ${\displaystyle (u,v)}$

• Pedali dell'ellisse

${\displaystyle a^{2}(u-x)^{2}+b^{2}(v-y)^{2}-(x^{2}+y^{2}-ux-vy)^{2}=0}$

ove l'ellisse è ${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}=1}$ e il punto pedale è ${\displaystyle (u,v)}$

• Pedali dell'iperbole

${\displaystyle a^{2}(u-x)^{2}-b^{2}(v-y)^{2}-(x^{2}+y^{2}-ux-vy)^{2}=0}$

ove l'iperbole è ${\displaystyle x^{2}/a^{2}-y^{2}/b^{2}=1}$ e il punto pedale è ${\displaystyle (u,v)}$

• 
  Curva a bicorno o a feluca
• 
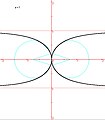  Curva a kappa o di Gutschoven
• 
  Pallottole punta a punta
• 
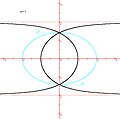  Trisettrice di Delange
• 
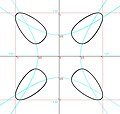  Curva di Edge quadriconnessa
• 
  Curva a uovo storto
• 
  Curva a uovo dritto
• 
  Uovo di Keplero
• 
  Curva a uovo doppio
• 
  Curva di Granville
• 
  Curva di Helton-Vinnikov
• 
  Curva di Klein
• 
  Curva a fagiolo o a pisello
• 
  Superellisse o Curva di Lamè
• 
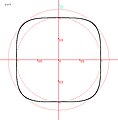  Supercerchio o Squircle
• 
  Curva a fiocco
• 
  Curva intrecciata
• 
  Curva a nodo
• 
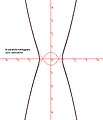  Campila di Eudosso
• 
  Curva cardioide
• 
  Curva Ampersand trinodata
• 
  Curva di Jerabek
• 
  Curva a svastica
• 
  Curva di Jubel
• 
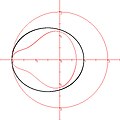  Ovale di Mandelbrot
• 
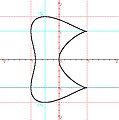  Curva bicuspidata
• 
  Curva deltoide o tricuspidata o di Steiner
• 
  Lemniscata di Bernoulli
• 
  Lemniscata di Gerono o Curva a ottoi
• 
  Lemniscata di Booth o Ippopede di Proclo
• 
  Curva di Wassenaar
• 
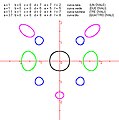  Curva Multiovale
• 
  Lumaca di Pascal o di Durer o Concoide del cerchio
• 
  Curva piriforme o a goccia d'acqua
• 
  Curve bifogliate
• 
  Curve trifogliate
• 
  Curva del diavolo
• 
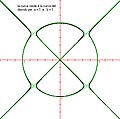  Motore elettrico
• 
  Curva Capricornoide
• 
  Perle di Sluze
• 
  Curva di Plucker
• 
  Curva a pesce
• 
  Concoide di Durer
• 
  Concoide di Kulp
• 
  Concoide di Nicomede
• 
  Curva cruciforme
• 
  Sezione spirica o di Perseo
• 
  Sezione torica
• 
  Ovali di Cartesio
• 
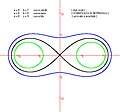  Ovali di Cassini
• 
  Curve di Jacobi
• 
  Curve di Edwards
• 
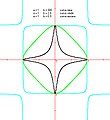  Curve di Edwards ritorte
• 
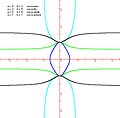  Curve di Edwards ritorte BIS
• 
  Curva di Trott a 28 bitangenti
• 
  Curva di Trott a 28 bitangenti BIS
• 
  Curva a 8 flessi
• 
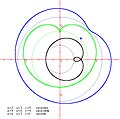  Pedali del cerchio
• 
  Pedali dell'ellisse
• 
  Pedali dell'iperbole

In Geometria descrittiva

Nella generalità dei casi, la quartica è una curve d'intersezione tra superfici quadriche. I punti di questa quartica si ottengono come punti comuni a sezioni complanari di tali superfici eseguite con un fascio di piani.

Le dette quartiche d'intersezione possono classificarsi secondo le seguenti situazioni reciproche:

• 1. Quando soltanto alcune generatrici di una superficie sono secanti l'altra, per cui la quartica in comune è formata da un solo ramo e viene detta monogrammica.
• 2. Quando tutte le generatrici di una superficie sono secanti l'altra. la quartica comune è composta da due rami detta digrammica.
• 3. Finestra di Viviani, un caso particolare di quartica digrammica, in cui una generatrice di una delle due superfici intersecanti, tange l'altra.

Le quartiche possono ammettere uno o due piani di simmetria, e questo dipende dalla reciproca posizione degli assi delle due superfici. Per esempio se gli assi sono complanari, la quartica d'intersezione ammette un piano di simmetria, la giacitura dell'altro piano di simmetria si riscontra nei casi in cui gli assi sono perpendicolari tra di loro.

La determinazione dei punti costituenti la quartica avviene con l'ausilio di un fascio di piani ausiliari secanti le due superfici. la scelta della giacitura di detti piani è fatta col fine di avere delle sezioni semplici da rappresentare. Ad esempio le sezioni con piani ortogonali all'asse di rotazione sono circonferenze e vengono rappresentate senza difficoltà se detto asse è perpendicolare ad uno dei piani di proiezione principali, altrimenti, si assumono altri piani di proiezione, ausiliari, di cui almeno uno abbia la giacitura perpendicolare all'asse; le sezioni proiettate su questi piani ausiliari risultano in vera forma

Voci correlate

• Curva quintica
• Curva sestica

Altri progetti

• Wikimedia Commons contiene immagini o altri file su curva quartica

Collegamenti esterni

• (EN) Breve definizione delle curve quartiche, su mathworld.wolfram.com.
• Programma per tracciare le curve quartiche, su ascifoni.com. URL consultato l'11 marzo 2012 (archiviato dall'url originale il 1º maggio 2015).
• Casi d'intersezione tra superfici di rotazione, su assex.altervista.org.

Controllo di autorità	Thesaurus BNCF 21714 · LCCN (EN) sh85034927 · BNF (FR) cb12267959v (data) · J9U (EN, HE) 987007538486305171