Himpunan Mandelbrot

Himpunan Mandelbrot adalah himpunan dari bilangan kompleks ${\displaystyle c}$ yang digunakan sebagai fungsi ${\displaystyle f_{c}(z)=z^{2}+c}$ tidak menyimpang ketika iterasi dari ${\displaystyle z=0}$, yaitu, urutan dari ${\displaystyle f_{c}(0)}$, ${\displaystyle f_{c}(f_{c}(0))}$, dll, tetap dibatasi dalam nilai absolut.

Definisinya dikreditkan ke Adrien Douady yang menamakannya sebagai penghormatan kepada matematikawan Benoit Mandelbrot.^[1] Himpunan tersebut terhubung ke sebuah himpunan Julia, dan himpunan Julia terkait menghasilkan bentuk fraktal yang kompleks serupa.

Gambar set Mandelbrot dapat dibuat dengan mengambil sampel bilangan kompleks dan pengujian, untuk setiap titik sampel ${\displaystyle c}$, apakah urutan dark ${\displaystyle f_{c}(0),f_{c}(f_{c}(0)),\dotsc }$ pergi ke tak terhingga (dalam praktik apakah itu meninggalkan beberapa lingkungan nilai yang telah ditentukan sebelumnya dari 0 setelah jumlah iterasi yang telah ditentukan). Bila bilangan riil dan bagian imajiner dari ${\displaystyle c}$ sebagai koordinat gambar pada bidang kompleks, piksel kemudian dapat diwarnai sesuai dengan seberapa cepat urutan dari ${\displaystyle |f_{c}(0)|,|f_{c}(f_{c}(0))|,\dotsc }$ melintasi ambang yang dipilih secara sewenang-wenang, dengan warna khusus (hitam) digunakan untuk nilai ${\displaystyle c}$ yang urutannya belum melewati ambang setelah jumlah iterasi yang ditentukan sebelumnya (ini diperlukan untuk membedakan dengan jelas gambar set Mandelbrot dari gambar pelengkap). Bila ${\displaystyle c}$ dipertahankan konstan dan nilai awal nilai ${\displaystyle z}$ dinotasikan dengan ${\displaystyle z_{0}}$ sebagai gantinya, variabel ini memperoleh nilai himpunan Julia untuk setiap titik ${\displaystyle c}$ di parameter spasi dari fungsinya.

Gambar dari himpunan Mandelbrot menunjukkan batas yang rumit dan sangat rumit yang mengungkapkan detail rekursif yang semakin halus pada perbesaran yang meningkat. Dengan kata lain, batas himpunan Mandelbrot adalah kurva fraktal. "Gaya" dari detail berulang ini bergantung pada wilayah himpunan yang sedang diperiksa. Batas himpunan juga menggabungkan versi yang lebih kecil dari bentuk utama, sehingga properti fraktal dari kemiripan diri berlaku untuk seluruh himpunan, dan tidak hanya untuk bagian-bagiannya.

Himpunan Mandelbrot telah menjadi populer di luar matematika baik karena daya tarik estetikanya maupun sebagai contoh struktur kompleks yang timbul dari penerapan aturan sederhana. Ini adalah salah satu contoh paling terkenal dari visualisasi matematika dan keindahan matematika.

Sejarah

Himpunan Mandelbrot berawal dari dinamika kompleks, bidang yang pertama kali diselidiki oleh matematikawan Prancis Pierre Fatou dan Gaston Julia pada awal abad ke 20. Fraktal ini pertama kali didefinisikan dan digambar pada tahun 1978 oleh Robert W. Brooks dan Peter Matelski sebagai bagian dari studi kelompok Kleinian..^[2] Pada tanggal 1 Maret 1980, di IBM Pusat Penelitian Thomas J. Watson di Yorktown Heights, New York, Benoit Mandelbrot pertama kali melihat visualisasi.^[3]

Mandelbrot mempelajari parameter space dari polinomial kuadrat dalam sebuah artikel yang muncul pada tahun 1980.^[4] Studi matematis himpunan Mandelbrot benar-benar dimulai dengan karya ahli matematika Adrien Douady dan John H. Hubbard (1985),^[1] yang menetapkan banyak properti fundamentalnya dan menamai himpunan tersebut untuk menghormati Mandelbrot atas karyanya yang berpengaruh di geometri fraktal.

Matematikawan Heinz-Otto Peitgen dan Peter Richter menjadi terkenal karena mempromosikan set dengan foto, buku (1986),^[5] dan pameran tur internasional Goethe-Institut Jerman (1985).^[6][7]

Artikel sampul pada Agustus 1985 Scientific American memperkenalkan algoritma kepada khalayak luas untuk menghitung himpunan Mandelbrot. Sampulnya menampilkan gambar yang terletak di −0.909 + −0.275 i dan diciptakan oleh Peitgen et al.^[8][9] Set Mandelbrot menjadi terkenal pada pertengahan 1980 an sebagai komputer demo grafis, ketika komputer pribadi menjadi cukup kuat untuk memplot dan menampilkan set dalam resolusi tinggi.^[10]

Karya Douady dan Hubbard bertepatan dengan peningkatan besar minat dalam dinamika kompleks dan matematika abstrak, dan studi tentang himpunan Mandelbrot telah menjadi pusat perhatian bidang ini. Daftar lengkap dari semua orang yang telah berkontribusi pada pemahaman himpunan ini sejak saat itu masih panjang, tetapi akan mencakup Mikhail Lyubich,^[11][12] Curt McMullen, John Milnor, Mitsuhiro Shishikura dan Jean-Christophe Yoccoz.

Definisi formal

Himpunan Mandelbrot adalah himpunan nilai c di bidang kompleks yang orbit dari nilai kritikal z = 0 di bawah Iteratal Kuadrat

${\displaystyle z_{n+1}=z_{n}^{2}+c}$

tetap dibatasi.^[13] Jadi, bilangan kompleks c adalah anggota himpunan Mandelbrot bila, saat dimulai dengan z₀ = 0 dan menerapkan iterasi berulang kali, nilai absolut dari z_n tetap terikat untuk semua n > 0.

Contohnya, untuk c = 1, urutannya adalah 0, 1, 2, 5, 26, ..., yang cenderung tak terhingga, jadi 1 bukan merupakan elemen himpunan Mandelbrot. Sebaliknya, untuk c=−1, urutannya adalah 0, −1, 0, −1, 0, ..., yang dibatasi, jadi −1 memang termasuk dalam himpunan.

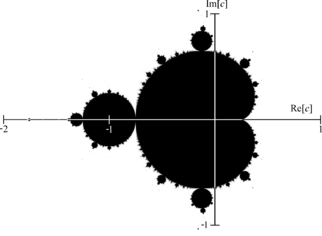
Set Mandelbrot juga bisa didefinisikan sebagai lokus keterhubungan dari keluarga polinomial.

Representasi grafis

Representasi grafis dari himpunan Mandelbrot dan strukturnya di area tepi hanya mungkin menggunakan komputer menggunakan apa yang disebut generator fraktal. Setiap piksel sesuai dengan nilai ${\displaystyle c}$ bidang kompleks. Untuk setiap piksel, komputer menentukan apakah urutan terkait divergen atau tidak. Begitu jumlahnya ${\displaystyle |z_{n}|}$ eines Anggota berurutan nilai ${\displaystyle s=2}$ melebihi, jelas bahwa hasilnya divergen. Nomor ${\displaystyle n}$ langkah iterasi sampai saat itu dapat berfungsi sebagai ukuran derajat divergensi. Pixel diberi warna sesuai dengan tabel warna yang telah ditentukan sebelumnya yang sesuai dengan setiap nilai ${\displaystyle n}$ memberikan warna.

Untuk mencapai batas yang harmonis antara warna-warna yang berurutan dari sudut pandang estetika, batas tersebut digunakan dalam praktiknya ${\displaystyle s}$ bukan nilai sekecil mungkin ${\displaystyle s=2}$ dipilih, tetapi nilai secara signifikan lebih besar dari ${\displaystyle 2}$, jika tidak, lebar garis warna akan berosilasi. Semakin besar nilai ini dipilih, semakin baik batas warna yang sesuai dengan garis ekuipotensial, yang dihasilkan ketika himpunan Mandelbrot diinterpretasikan sebagai bermuatan listrik konduktor. Untuk gradien warna kontinu, Seperti pada rangkaian gambar zoom di atas, evaluasi faktor diperlukan di mana ${\displaystyle s}$ terlampaui saat nilainya dilampaui untuk pertama kalinya.

Karena jumlah langkah iterasi ${\displaystyle n}$, setelah itu batasnya ${\displaystyle s}$ terlampaui, dapat berukuran berapa pun, kriteria penghentian dalam bentuk jumlah langkah iterasi maksimum harus ditentukan. Nilai ${\displaystyle c}$, konsekuensi yang belum melebihi batas ${\displaystyle s}$ setelahnya menjadi ${\displaystyle \mathbb {M} }$ diharapkan. Semakin kecil jarak ${\displaystyle c}$ zu ${\displaystyle \mathbb {M} }$ adalah, semakin besar angka ${\displaystyle n}$ biasanya setelah ${\displaystyle s}$ terlampaui. Semakin besar pembesaran tepi ${\displaystyle \mathbb {M} }$ ditampilkan, semakin besar jumlah maksimum langkah iterasi yang harus dipilih, dan semakin banyak waktu komputasi yang diperlukan. Dapat dilihat bahwa urutan nilai awal ${\displaystyle c}$ konvergen, perhitungan urutannya bisa diakhiri lebih awal.

Representasi tepi secara grafis sangat menarik ${\displaystyle \mathbb {M} }$ dengan kekayaan bentuknya. Semakin besar perbesaran yang dipilih, struktur yang lebih kompleks dapat ditemukan di sana. Dengan program komputer yang sesuai, tepi ini dapat ditampilkan seperti pada mikroskop dengan perbesaran apa pun. Hanya dua kebebasan artistik yang ada adalah pemilihan bagian gambar dan penetapan warna pada tingkat divergensi.

Perbesaran sering kali diperlukan untuk memeriksa struktur yang diinginkan, yang tidak dapat dihitung dengan tipe data yang didukung perangkat keras karena keakuratannya yang terbatas. Oleh karena itu, beberapa program berisi tipe data bilangan panjang aritmatika dengan presisi yang dapat dipilih secara sewenang-wenang. Ini berarti bahwa (hampir) semua faktor pembesaran dimungkinkan.

Properti dasar

Himpunan Mandelbrot adalah himpunan kompak, karena ia tertutup dan terkandung dalam disk tertutup dengan radius 2 di sekitar asal. Lebih khusus lagi, satu poin ${\displaystyle c}$ termasuk dalam kumpulan Mandelbrot jika dan hanya jika

${\displaystyle |P_{c}^{n}(0)|\leq 2}$ untuk semua ${\displaystyle n\geq 0.}$

Dengan kata lain, nilai absolut dari ${\displaystyle P_{c}^{n}(0)}$ harus tetap pada atau di bawah 2 untuk ${\displaystyle c}$ berada di himpunan Mandelbrot, seolah-olah nilai absolut itu melebihi 2, urutannya akan lolos hingga tak terbatas.

persimpangan dari ${\displaystyle M}$ dengan sumbu nyata tepatnya adalah interval [−2, 1/4]. Parameter sepanjang interval ini dapat dimasukkan ke dalam korespondensi satu-satu dengan yang ada di keluarga logistik yang sebenarnya,

${\displaystyle x_{n+1}=rx_{n}(1-x_{n}),\quad r\in [1,4].}$

Korespondensi diberikan oleh

${\displaystyle z=r\left({\frac {1}{2}}-x\right),\quad c={\frac {r}{2}}\left(1-{\frac {r}{2}}\right).}$

Faktanya, ini memberikan korespondensi antara seluruh ruang parameter dari keluarga logistik dan yang ada di himpunan Mandelbrot.

Douady dan Hubbard telah menunjukkan bahwa set Mandelbrot adalah terhubung. Faktanya, mereka membangun sebuah isomorfisma konformal antara komplemen himpunan Mandelbrot dan komplemen disk unit tertutup. Mandelbrot awalnya menduga bahwa set Mandelbrot adalah terputus. Dugaan ini didasarkan pada gambar komputer yang dihasilkan oleh program yang tidak dapat mendeteksi filamen tipis yang menghubungkan berbagai bagian ${\displaystyle M}$. Setelah percobaan lebih lanjut, dia merevisi dugaannya, memutuskan itu ${\displaystyle M}$ harus terhubung. Ada juga bukti topologi untuk keterhubungan yang ditemukan pada tahun 2001 oleh Jeremy Kahn.^[14]

Rumus dinamis untuk penyeragaman dari pelengkap himpunan Mandelbrot, yang muncul dari bukti Douady dan Hubbard tentang keterkaitan ${\displaystyle M}$, memunculkan sinar eksternal dari himpunan Mandelbrot. Sinar ini dapat digunakan untuk mempelajari himpunan Mandelbrot dalam istilah kombinatorial dan membentuk tulang punggung Jean-Christophe Yoccoz#pekerjaan Matematika.^[15]

batas dari himpunan Mandelbrot persis lokus percabangan dari keluarga kuadrat; yaitu, kumpulan parameter ${\displaystyle c}$ di mana dinamika berubah secara tiba-tiba di bawah perubahan kecil ${\displaystyle c.}$ Itu dapat dibangun sebagai himpunan batas dari urutan bidang kurva aljabar, yang kurva Mandelbrot, dari tipe umum yang dikenal sebagai lemniskat polinomial. Kurva Mandelbrot ditentukan oleh pengaturan p₀ = z, p_n+1 = p_n² + z, dan kemudian menafsirkan kumpulan poin |p_n(z)| = 2 dalam bidang kompleks sebagai kurva dalam bidang Cartesian derajat 2ⁿ⁺¹ in x and y. Kurva aljabar ini muncul dalam gambar set Mandelbrot yang dihitung menggunakan "algoritme waktu melarikan diri" yang disebutkan di bawah.

Perilaku deretan angka

Berbagai elemen struktural ${\displaystyle \mathbb {M} }$ terkait erat dengan perilaku tertentu dari urutan angka, itu ${\displaystyle \mathbb {M} }$ yang mendasari. Bergantung pada nilai ${\displaystyle c}$, ada empat kemungkinan:

• Bila nilai menyatu ke titik tetap.
• Ketika menyatu dengan siklus batas periodik yang terdiri dari dua atau lebih nilai. Ini juga mencakup kasus di mana urutan berperilaku secara berkala sejak awal.
• Karena hal ini tidak pernah berulang, tetapi tetap terbatas. Beberapa nilai menunjukkan perilaku kacau dengan pergantian antara siklus batas hampir periodik dan perilaku acak.
• Terutama menyimpang menuju tak terbatas (divergensi tertentu).

Semua ${\displaystyle c}$ nilai yang tidak pasti dimiliki secara berbeda ${\displaystyle \mathbb {M} }$.

Tabel berikut menunjukkan contoh dari empat perilaku batas iterasi nilai ${\displaystyle z_{n+1}=z_{n}^{2}+c}$ dari ${\displaystyle z_{0}=0}$:

Parameter	Nilai ${\displaystyle z_{2},z_{3},z_{4},z_{5},\ldots }$	Titik tetap
Nilai sumbu riil...
${\displaystyle c=-3}$	${\displaystyle 6,\,33,\,1086,\,1179393,\,\dotsc }$	Perbedaan nilai tertentu ${\displaystyle +\infty }$
${\displaystyle c=-2}$	${\displaystyle 2,\,2,\,2,\,2,\,\dotsc }$	Konvergensi tetap menuju titik kontinu ${\displaystyle 2}$
${\displaystyle c=-1{,}75}$	${\displaystyle {\tfrac {21}{16}},\,-{\tfrac {7}{256}},\,-{\tfrac {114639}{65536}},\,\dotsc }$	Konvergensi tetap ke siklus tiga urutan ${\displaystyle -1{,}74697\ldots ,\,1{,}30193\ldots ,\,-0{,}54958\ldots }$
${\displaystyle c=-1{,}5}$	${\displaystyle {\tfrac {3}{4}},\,-{\tfrac {15}{16}},\,-{\tfrac {159}{256}},\,-{\tfrac {73023}{65536}},\,\dotsc }$	Chaotisches Verhalten
${\displaystyle c=-1{,}4}$	${\displaystyle 0{,}56,\,-1{,}0864,\,-0{,}21973504,\,\dotsc }$	Konvergensi tetap 32 ke siklus batas
${\displaystyle c=-1{,}25}$	${\displaystyle {\tfrac {5}{16}},\,-{\tfrac {295}{256}},\,{\tfrac {5105}{65536}},\,\dotsc }$	Konvergensi terhadap siklus urutan bolak-balik ${\displaystyle -1{,}20710\ldots ,\,0{,}20710\ldots }$
${\displaystyle c=-1}$	${\displaystyle -1,\,0,\,-1,\,0,\,-1,\,0,\,\dotsc }$	Konvergensi instan tidak tetap siklus urutan bolak-balik ${\displaystyle -1,\,0}$
${\displaystyle c=-0{,}75}$	${\displaystyle -{\tfrac {3}{16}},\,-{\tfrac {183}{256}},\,-{\tfrac {15663}{65536}},\,\dotsc }$	Konvergensi agak tetap menuju titik tertentu ${\displaystyle -{\tfrac {1}{2}}}$
${\displaystyle c=-0{,}5}$	${\displaystyle -{\tfrac {1}{4}},\,-{\tfrac {7}{16}},\,-{\tfrac {79}{256}},\,-{\tfrac {26527}{65536}},\,\dotsc }$	Konvergensi titik tetap ${\displaystyle {\tfrac {1}{2}}-{\sqrt {\tfrac {3}{4}}}}$
${\displaystyle c=-0{,}25}$	${\displaystyle -{\tfrac {3}{16}},\,-{\tfrac {55}{256}},\,-{\tfrac {13359}{65536}},\,\dotsc }$	Nilai titik tetap konvergensi ${\displaystyle {\tfrac {1}{2}}-{\sqrt {\tfrac {1}{2}}}}$
${\displaystyle c=0}$	${\displaystyle 0,\,0,\,0,\,0,\,0,\,0,\,\dotsc }$	Konvergensi melawan titik tetap ${\displaystyle 0}$
${\displaystyle c=+0{,}25}$	${\displaystyle {\tfrac {5}{16}},\,{\tfrac {89}{256}},\,{\tfrac {24305}{65536}},\,\dotsc }$	Konvergensi menuju titik tetap ${\displaystyle {\tfrac {1}{2}}}$
${\displaystyle c=+1}$	${\displaystyle 2,\,5,\,26,\,677,\,458330,\,\dotsc }$	Perbedaan tertentu pada nilai tetap ${\displaystyle +\infty }$
Dalam bidang bilangan kompleks...
${\displaystyle c=-i}$	${\displaystyle -1-i,\,i,\,-1-i,\,i,\,\dotsc }$	Konvergensi instan melawan siklus batas bolak-balik ${\displaystyle -1-i,\,i}$
${\displaystyle c=-{\tfrac {1}{8}}+{\tfrac {3}{4}}i}$	${\displaystyle -{\tfrac {43}{64}}+{\tfrac {9}{16}}i}$	Konvergensi menuju siklus tiga batas

Penilaian geometris

Konvergensi terjadi tepat untuk nilai ${\displaystyle c}$ yang menyusun interior kardioid, "tubuh" dari ${\displaystyle \mathbb {M} }$, serta untuk banyak titik batas mereka yang tak terhitung banyaknya. Siklus batas periodik dapat ditemukan pada (kurang lebih) "rintisan" dari nilai melingkar seperti pada "kepala", di kardioid satelit serta di banyak titik tepi komponen ini. Sebuah dugaan fundamental mengatakan bahwa ada siklus batas untuk semua titik dalam himpunan Mandelbrot. Urutannya benar-benar pra-periodik untuk banyak parameter yang tak terhitung banyaknya, yang sering disebut Titik Misiurewicz-Thurston (setelah Michał Misiurewicz dan William Thurston). Ini termasuk "ujung antena" seperti titik ${\displaystyle z=-2}$ paling kiri dan titik cabang himpunan Mandelbrot.

Dalam banyak titik lain dari himpunan Mandelbrot yang tak terhitung banyaknya, urutan dapat berperilaku dalam berbagai cara, yang masing-masing menghasilkan sistem dinamis yang sangat berbeda dan sebagian menjadi subjek penelitian intensif. Je menurut definisi kata tersebut, perilaku "kacau" dapat ditemukan.

Properti lainnya

Geometri

Kardioid mempunyai periode 1. Lingkaran mempunyai periode selain 1, kecuali mini mandelbrot yang ada di c = -1,75.

Generalisasi

Animasi Himpunan Multibrot untuk d dari 0 hingga 5 (kiri) dan dari 0,05 hingga 2 (kanan).

Himpunan Multibrot

Himpunan Multibrot adalah himpunan berbatas yang ditemukan di bidang kompleks untuk anggota famili rekursi monik univariat polinomial umum

${\displaystyle z\mapsto z^{d}+c.\ }$

Untuk integer d, himpunan ini adalah lokus keterhubungan untuk himpunan Julia yang dibangun dari rumus yang sama. Lokus keterhubungan kubik penuh juga telah dipelajari; di sini orang menganggap dua parameter berulang ${\displaystyle z\mapsto z^{3}+3kz+c}$, yang dua titik kritikal adalah akar kuadrat kompleks dari parameter k. Parameter berada dalam lokus keterhubungan kubik jika kedua titik kritis stabil.^[16] Untuk famili umum holomorphic function, boundary dari himpunan Mandelbrot digeneralisasikan ke lokus percabangan, yang merupakan objek alami untuk dipelajari bahkan ketika lokus keterhubungan tidak berguna.

Lihat pula

• Buddhabrot
• Fraktal collatz
• Fractint
• Perubahan Gilbreath
• Mandelbox
• Mandelbulb
• Menger Sponge
• Fraktal Newton
• Potret orbit
• Orbit trap
• Pickover stalk

Referensi

Bacaan lebih lanjut

• John W. Milnor, Dynamics in One Complex Variable (Third Edition), Annals of Mathematics Studies 160, (Princeton University Press, 2006), ISBN 0-691-12488-4
  (First appeared in 1990 as a Stony Brook IMS Preprint, available as arXiV:math.DS/9201272 )
• Nigel Lesmoir-Gordon, The Colours of Infinity: The Beauty, The Power and the Sense of Fractals, ISBN 1-904555-05-5
  (includes a DVD featuring Arthur C. Clarke and David Gilmour)
• Heinz-Otto Peitgen, Hartmut Jürgens, Dietmar Saupe, Chaos and Fractals: New Frontiers of Science (Springer, New York, 1992, 2004), ISBN 0-387-20229-3

Pranala luar

Wikibooks memiliki buku di:

Fraktal