Théorème de Taylor

Page d’aide sur l’homonymie

Pour les articles homonymes, voir Taylor.

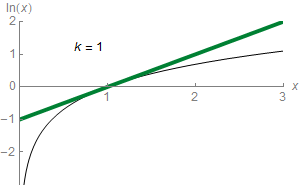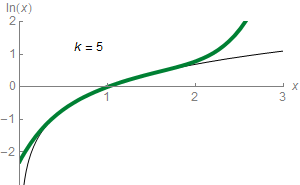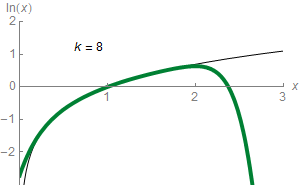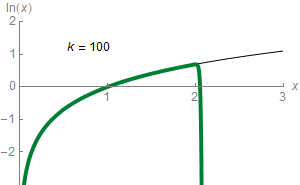
Représentation de la fonction logarithme (en noir) et des approximations de Taylor au point 1 (en vert).

En mathématiques, plus précisément en analyse, le théorème de Taylor (ou formule de Taylor), du nom du mathématicien anglais Brook Taylor qui l'établit en 1715, montre qu'une fonction plusieurs fois dérivable au voisinage d'un point peut être approchée par une fonction polynomiale dont les coefficients dépendent uniquement des dérivées de la fonction en ce point. Cette fonction polynomiale est parfois appelée polynôme de Taylor.

Définition

Formulation standard

De manière plus précise, soit :

  • I {\displaystyle I} un intervalle réel ;
  • a {\displaystyle a} un élément de I {\displaystyle I}  ;
  • E {\displaystyle E} un espace vectoriel normé réel ;
  • f {\displaystyle f} une fonction de I {\displaystyle I} dans E {\displaystyle E} dérivable en a {\displaystyle a} jusqu'à un certain ordre n ≥ 1 {\displaystyle n\geq 1} .

Alors pour tout nombre réel x {\displaystyle x} appartenant à I {\displaystyle I} , on a la formule de Taylor-Young (voir infra) :

f ( x ) = f ( a ) + f ′ ( a ) 1 ! ( x − a ) + f ( 2 ) ( a ) 2 ! ( x − a ) 2 + ⋯ + f ( n ) ( a ) n ! ( x − a ) n + R n ( x ) {\displaystyle f(x)=f(a)+{\frac {f'(a)}{1!}}\,(x-a)+{\frac {f^{(2)}(a)}{2!}}\,(x-a)^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}\,(x-a)^{n}+R_{n}(x)}

ou de façon équivalente :

f ( x ) = ∑ k = 0 n f ( k ) ( a ) k ! ( x − a ) k + R n ( x ) {\displaystyle f(x)=\sum _{k=0}^{n}{\frac {f^{(k)}(a)}{k!}}\,(x-a)^{k}+R_{n}(x)}

où le reste R n ( x ) {\displaystyle R_{n}(x)} est une fonction négligeable par rapport à ( x − a ) n {\displaystyle (x-a)^{n}} au voisinage de a {\displaystyle a} .

Autre formulation

Par changement de variable de x {\displaystyle x} en a + h {\displaystyle a+h} , la formule de Taylor-Young peut aussi s'exprimer sous la forme :

f ( a + h ) = f ( a ) + f ′ ( a ) 1 ! h + f ( 2 ) ( a ) 2 ! h 2 + ⋯ + f ( n ) ( a ) n ! h n + R n ( a + h ) {\displaystyle f(a+h)=f(a)+{\frac {f'(a)}{1!}}\,h+{\frac {f^{(2)}(a)}{2!}}\,h^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}\,h^{n}+R_{n}(a+h)}

ou de façon équivalente :

f ( a + h ) = ∑ k = 0 n f ( k ) ( a ) k ! h k + R n ( a + h ) {\displaystyle f(a+h)=\sum _{k=0}^{n}{\frac {f^{(k)}(a)}{k!}}\,h^{k}+R_{n}(a+h)}

où le reste R n ( a + h ) {\displaystyle R_{n}(a+h)} est une fonction négligeable par rapport à h n {\displaystyle h^{n}} au voisinage de 0 (c'est-à-dire pour h {\displaystyle h} petit).

Expressions et estimations du reste

En présentant cette formule en 1715[1],[2],[3], Taylor propose ainsi une méthode de développement en série[4], mais sans se préoccuper du reste R n ( x ) {\displaystyle R_{n}(x)} . En effet, pendant tout le XVIIIe siècle, les mathématiciens n'établissent pas encore de différence entre développement limité et développement en série entière. C'est Joseph-Louis Lagrange qui, en 1799, souligne le premier la nécessité de définir rigoureusement ce reste[5],[6]. Les propriétés de celui-ci s'énoncent différemment selon les hypothèses sur la fonction.

Formule de Taylor-Young

La formule de Taylor-Young porte le nom de William Henry Young.

Si la fonction f {\displaystyle f} (à valeurs réelles ou complexes, ou même dans un espace normé) est dérivable en a {\displaystyle a} jusqu'à l'ordre n ≥ 1 {\displaystyle n\geq 1} , alors la fonction R n ( x ) {\displaystyle R_{n}(x)} est négligeable devant ( x − a ) n {\displaystyle (x-a)^{n}}  :

R n ( x ) = o ( ( x − a ) n ) . {\displaystyle {R_{n}(x)}=o({(x-a)^{n}}).}

La formulation suivante est équivalente :

lim x → a x ≠ a R n ( x ) ( x − a ) n = 0. {\displaystyle \lim _{x\to a \atop x\neq a}{\frac {R_{n}(x)}{(x-a)^{n}}}=0.}

L'énoncé se démontre par récurrence simple, à l'aide d'une « intégration » terme à terme d'un développement limité[7], ou encore par application itérée de la règle de l'Hôpital[8].

Formule de Taylor-Lagrange

La formule de Taylor-Lagrange porte le nom de Joseph Louis Lagrange.

Si la fonction f {\displaystyle f} est à valeurs réelles et est dérivable sur I {\displaystyle I} jusqu'à l'ordre n + 1 {\displaystyle n+1} , alors, pour tout x ∈ I ∖ { a } {\displaystyle x\in I\setminus \{a\}} , il existe un nombre réel ξ {\displaystyle \xi } strictement compris entre a {\displaystyle a} et x {\displaystyle x} tel que

R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − a ) n + 1 . {\displaystyle R_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\,(x-a)^{n+1}.}

Cette relation s'appelle également la forme de Lagrange. L'existence de ξ {\displaystyle \xi } se déduit directement[7] du théorème de Rolle (ou de sa variante, le théorème des accroissements finis[9]).

Le nombre ξ {\displaystyle \xi } est parfois noté a + ( x − a ) θ {\displaystyle a+(x-a)\theta } , et la condition qu'il soit compris entre a {\displaystyle a} et x {\displaystyle x} s'écrit alors 0 < θ < 1 {\displaystyle 0<\theta <1} .

Inégalité de Taylor-Lagrange

S'il existe M {\displaystyle M} tel que

∀ y ∈ I | f ( n + 1 ) ( y ) | ≤ M , {\displaystyle \forall y\in I\quad |f^{(n+1)}(y)|\leq M,}

alors, pour tout x ∈ I {\displaystyle x\in I}  :

| R n ( x ) | ≤ M | x − a | n + 1 ( n + 1 ) ! . {\displaystyle |R_{n}(x)|\leq {\frac {M|x-a|^{n+1}}{(n+1)!}}.}

Formule de Taylor-Cauchy

La formule de Taylor-Cauchy porte le nom d'Augustin Louis Cauchy.

C'est une variante de la formule de Taylor-Lagrange[9],[10]. Si la fonction f {\displaystyle f} est à valeurs réelles et qu'elle est dérivable sur I {\displaystyle I} jusqu'à l'ordre n + 1 {\displaystyle n+1} alors, pour tout x ∈ I ∖ { a } {\displaystyle x\in I\setminus \{a\}} , il existe un nombre ξ {\displaystyle \xi } strictement compris entre a {\displaystyle a} et x {\displaystyle x} tel que

R n ( x ) = f ( n + 1 ) ( ξ ) n ! ( x − a ) ( x − ξ ) n . {\displaystyle R_{n}(x)={\frac {f^{(n+1)}(\xi )}{n!}}\,(x-a)\,(x-\xi )^{n}.}

Formule de Taylor avec reste intégral de Laplace

La formule de Taylor avec reste intégral de Laplace porte le nom de Pierre-Simon de Laplace.

Si la fonction f {\displaystyle f} est de classe C n + 1 {\displaystyle {\mathcal {C}}^{n+1}} sur I {\displaystyle I} et à valeurs dans un espace de Banach réel, alors, pour tout x ∈ I {\displaystyle x\in I}  :

R n ( x ) = ∫ a x f ( n + 1 ) ( t ) n ! ( x − t ) n d t . {\displaystyle R_{n}(x)=\int _{a}^{x}{\frac {f^{(n+1)}(t)}{n!}}\,(x-t)^{n}\,\mathrm {d} t.}

Cet énoncé se démontre par récurrence, à l'aide d'une intégration par parties[7].

Remarques

Formule de Taylor-Maclaurin : lorsque a {\displaystyle a} = 0, la formule s’écrit

f ( x ) = f ( 0 ) + f ′ ( 0 ) 1 ! x + f ( 2 ) ( 0 ) 2 ! x 2 + ⋯ + f ( n ) ( 0 ) n ! x n + R n ( x ) . {\displaystyle f(x)=f(0)+{\frac {f'(0)}{1!}}\,x+{\frac {f^{(2)}(0)}{2!}}\,x^{2}+\cdots +{\frac {f^{(n)}(0)}{n!}}\,x^{n}+R_{n}(x).}

Contrairement à la formule de Taylor-Lagrange, les théorèmes de Taylor-Young et de Taylor-Laplace sont vrais pour des fonctions f {\displaystyle f} à valeurs complexes ou dans un espace vectoriel normé, complet pour pouvoir parler d'intégrale (de Bochner) pour le second.

Pour une fonction à valeurs réelles, l'inégalité de Taylor-Lagrange est un corollaire immédiat de la formule de Taylor-Lagrange. Pour une fonction à valeurs dans un espace vectoriel normé, on ne dispose pas de cette formule mais on peut déduire l'inégalité de Taylor-Lagrange de l'inégalité des accroissements finis pour les fonctions à valeurs vectorielles.

La formule de Taylor-Lagrange pour n = 0 {\displaystyle n=0} est le théorème des accroissements finis.

La formule de Taylor avec reste de Laplace est une généralisation du second théorème fondamental de l'analyse.

Pour certaines fonctions f {\displaystyle f} , le reste R n ( x ) {\displaystyle R_{n}(x)} tend vers zéro lorsque n {\displaystyle n} tend vers l'infini ; ces fonctions peuvent ainsi être développées en série de Taylor dans un voisinage du point a {\displaystyle a} . Si cette propriété se vérifie en tout point du domaine de définition, la fonction est dite analytique.

Formule de Taylor pour les fonctions de plusieurs variables

La formule de Taylor est extensible aux fonctions de plusieurs variables.

Formule de Taylor-Young dans les espaces vectoriels normés[11],[12] — Soient E {\displaystyle E} et F {\displaystyle F} deux espaces vectoriels normés.

Si une fonction f : E → F {\displaystyle f:E\to F} est n {\displaystyle n} fois différentiable en un point a ∈ E {\displaystyle a\in E} , alors elle admet en ce point un développement limité à l'ordre n {\displaystyle n} , donné par

f ( a + h ) = f ( a ) + d f a ( h ) + 1 2 ! d 2 f a ( h 2 ) + ⋯ + 1 n ! d n f a ( h n ) + o ( ‖ h ‖ n ) {\displaystyle f(a+h)=f(a)+\mathrm {d} f_{a}(h)+{\frac {1}{2!}}\,\mathrm {d} ^{2}f_{a}\left(h^{2}\right)+\dots +{\frac {1}{n!}}\,\mathrm {d} ^{n}f_{a}\left(h^{n}\right)+o\left(\|h\|^{n}\right)}

où h k {\displaystyle h^{k}} désigne le k {\displaystyle k} -uplet ( h , … , h ) ∈ E k {\displaystyle (h,\dots ,h)\in E^{k}} .

Exemple :

Pour une fonction f : R p → R {\displaystyle f:\mathbb {R} ^{p}\to \mathbb {R} } deux fois différentiable en a ∈ R p {\displaystyle a\in \mathbb {R} ^{p}} , on a :

f ( a + h ) = f ( a ) + ∇ f ( a ) ⋅ h + 1 2 h T H ( a ) h + o ( ‖ h ‖ 2 ) {\displaystyle f(a+h)=f(a)+\nabla f(a)\cdot h+{\frac {1}{2}}\,h^{T}\,\mathbb {H} (a)\,h+o(\|h\|^{2})}

où ∇ f {\displaystyle \nabla f} est le gradient de f {\displaystyle f} et H ( a ) {\displaystyle \mathbb {H} (a)} est sa matrice hessienne évaluée en a {\displaystyle a} .

Ceci se réécrit « en coordonnées » : par exemple pour une fonction f : R 2 → R {\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} } deux fois différentiable en ( a , b ) ∈ R 2 {\displaystyle (a,b)\in \mathbb {R} ^{2}} , on a :

f ( a + h , b + k ) = f ( a , b ) + ∂ f ∂ x ( a , b ) h + ∂ f ∂ y ( a , b ) k + 1 2 ∂ 2 f ∂ x 2 ( a , b ) h 2 + 1 2 ∂ 2 f ∂ y 2 ( a , b ) k 2 + ∂ 2 f ∂ x ∂ y ( a , b ) h k + o ( h 2 + k 2 ) . {\displaystyle {\begin{aligned}f(a+h,b+k)=f(a,b)&+{\frac {\partial f}{\partial x}}(a,b)\,h+{\frac {\partial f}{\partial y}}(a,b)\,k+{\frac {1}{2}}{\frac {\partial ^{2}f}{\partial x^{2}}}(a,b)\,h^{2}\\&+{\frac {1}{2}}{\frac {\partial ^{2}f}{\partial y^{2}}}(a,b)\,k^{2}+{\frac {\partial ^{2}f}{\partial x\partial y}}(a,b)\,hk\\&+o(h^{2}+k^{2}).\end{aligned}}}

On peut de même développer « en coordonnées » la formule de Taylor-Young globale ci-dessus, pour des fonctions n {\displaystyle n} fois différentiables en un point a {\displaystyle a} de R p {\displaystyle \mathbb {R} ^{p}} et à valeurs dans R {\displaystyle \mathbb {R} } (ou dans n'importe quel espace vectoriel normé). On voit apparaître des coefficients multinomiaux.

On a également une inégalité de Taylor-Lagrange dans les espaces vectoriels normés[13] qui, développée « en coordonnées » dans le cas particulier E = R p {\displaystyle E=\mathbb {R} ^{p}} et F = R {\displaystyle F=\mathbb {R} } , donne :

Soient O {\displaystyle O} un ouvert de R p {\displaystyle \mathbb {R} ^{p}} et f {\displaystyle f} une fonction n + 1 {\displaystyle n+1} fois différentiable de O {\displaystyle O} dans R {\displaystyle \mathbb {R} } . Alors pour tout [ a , x ] ⊂ O {\displaystyle \left[a,x\right]\subset O}  :

f ( x ) = ∑ | α | = 0 n 1 α ! ∂ α f ( a ) ∂ x α ( x − a ) α + ∑ | α | = n + 1 R α ( x ) ( x − a ) α {\displaystyle f(x)=\sum _{|\alpha |=0}^{n}{\frac {1}{\alpha !}}\,{\frac {\partial ^{\alpha }f(a)}{\partial x^{\alpha }}}\,(x-a)^{\alpha }+\sum _{|\alpha |=n+1}R_{\alpha }(x)\,(x-a)^{\alpha }}

où les sommes portent sur les multi-indices α {\displaystyle \alpha } , et où le reste vérifie l'inégalité

| R α ( x ) | ≤ sup y ∈ [ a , x ] | 1 α ! ∂ α f ( y ) ∂ x α | {\displaystyle |R_{\alpha }(x)|\leq \sup _{y\in \left[a,x\right]}\left|{\frac {1}{\alpha !}}\,{\frac {\partial ^{\alpha }f(y)}{\partial x^{\alpha }}}\right|}

pour tous les α {\displaystyle \alpha } tels que | α | = n + 1 {\displaystyle |\alpha |=n+1} (si f {\displaystyle f} est de classe C n + 1 {\displaystyle {\mathcal {C}}^{n+1}} , le majorant ci-dessus est fini).

Notes et références

  1. ↑ Taylor, Methodus incrementorum directa & inversa, Prop.VII, theo. III, p. 21.
  2. ↑ Voir à ce sujet l'article « Brook Taylor ».
  3. ↑ Dans son ouvrage Calcolo differenziale e principii di calcolo integrale (1884), p. XVII, Giuseppe Peano signale qu'en 1694, Jean Bernoulli donna une formule équivalente à la formule de Taylor. Cf. Jean Bernoulli, Additamentum effectionis omnium quadraturarum & rectificationum curvarum per seriem quandam generalissimam, Opera Omnia, t. I, p. 126.
  4. ↑ (en) Brook Taylor (trad. Ian Bruce), Methodus incrementorum directe et inversa, proposition VII, théorème III, corollaire II, Londres, 1715 [lire en ligne].
  5. ↑ Jean-Luc Chabert et al., Histoire d'algorithmes, du caillou à la puce, Belin, 1993, p.455
  6. ↑ Joseph-Louis Lagrange, Leçons sur le calcul des fonctions, 1799, réédité en 1806, leçon neuvième, p. 88 : « Tant que ce développement ne sert qu'à la génération des fonctions dérivées, il est indifférent que la série aille à l'infini ou non ; il l'est aussi lorsqu'on ne considère le développement que comme une simple transformation analytique de la fonction ; mais, si on veut l'employer pour avoir la valeur de la fonction dans les cas particuliers, comme offrant une expression d'une forme plus simple […], alors, ne pouvant tenir compte que d'un certain nombre plus ou moins grand de termes, il est important d'avoir un moyen d'évaluer le reste de la série qu'on néglige, ou du moins de trouver des limites de l'erreur qu'on commet en négligeant ce reste. »
  7. ↑ a b et c Voir par exemple le paragraphe « Formules de Taylor » du chapitre « Développements limités » sur Wikiversité.
  8. ↑ Voir par exemple cet exercice corrigé de la leçon « Fonctions d'une variable réelle » sur Wikiversité.
  9. ↑ a et b Formules de Taylor, cours de Jean-François Burnol.
  10. ↑ (en) Eric W. Weisstein, « Cauchy Remainder », sur MathWorld.
  11. ↑ (en) Rodney Coleman, Calculus on Normed Vector Spaces, Springer, (lire en ligne), p. 108.
  12. ↑ Pour une démonstration, voir par exemple « Formule de Taylor-Young » dans la leçon « Calcul différentiel » sur Wikiversité.
  13. ↑ Coleman 2012, p. 110.

Bibliographie

  • Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de mathématiques, t. 2 : Analyse, Bordas, .
  • Claude Deschamps et André Warusfel, J'intègre, Mathématiques première année, Dunod, .
  • Joseph-Louis Lagrange, Théorie des fonctions analytiques contenant les principes du calcul différentiel, dégagés de toute considération d'infiniment petits ou d'évanouissants, de limites ou de fluxions et réduits à l'analyse algébrique des quantités finies (1797), Journal de l'École polytechnique, 9e cahier, t. III, § 52, p. 49.

Voir aussi

Sur les autres projets Wikimedia :

  • Formules de Taylor, sur Wikiversity
  • icône décorative Portail de l'analyse