Suite de Fibonacci

En mathématiques, la suite de Fibonacci est une suite de nombres entiers dans laquelle chaque nombre est la somme des deux nombres qui le précèdent. Elle commence par les nombres 0 et 1^[1] puis se poursuit avec 1 (comme somme de 0 et 1), 2 (comme somme de 1 et 1), 3 (comme somme de 1 et 2), 5 (comme somme de 2 et 3), 8 (comme somme de 3 et 5), etc. Les termes de cette suite, i.e. les nombres apparaissant dans cette suite, sont appelés nombres de Fibonacci.

La suite de Fibonacci est répertoriée comme suite A000045 de l'OEIS.

Elle est liée au nombre d'or, noté φ (phi), qui intervient dans l'expression du terme général de la suite. Inversement, la suite de Fibonacci intervient dans l'écriture des réduites de l'expression de φ en fraction continue : les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or.

Définition formelle

La suite de Fibonacci ${\displaystyle (F_{n})_{n\in \mathbb {N} }}$ est définie par ${\displaystyle F_{0}=0,\quad F_{1}=1}$, et la relation de récurrence ${\displaystyle F_{n}=F_{n-1}+F_{n-2}}$ pour ${\displaystyle n\geqslant 2}$. Le tableau suivant donne les 15 premiers termes de la suite de Fibonacci :

F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	...	Fn
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	...	Fn – 1 + Fn – 2

Dans cet article, nous avons fait commencer la suite à ${\displaystyle n=0}$ avec ${\displaystyle F_{0}=0}$, comme le fait Edouard Lucas^[1]. D'autres auteurs font débuter la suite à 1^[2] : ${\displaystyle f_{0}=f_{1}=1,f_{2}=2,f_{3}=3,f_{4}=5}$, etc. Le nombre F_n s'appelle parfois le n-ième nombre de Fibonacci^[2] (bien qu'il soit techniquement le n+1-ième si on commence à 0).

Histoire

En Inde

Dans la branche des mathématiques concernant la combinatoire, les mathématiciens indiens s'intéressent à des problèmes de lexicographie et de métrique. Le mètre āryā (en) est composé de syllabes pouvant être brèves (de longueur un mātrā, cf. alphasyllabaire) ou longues (de longueur deux mātrās). La question est de savoir comment peuvent s'alterner les brèves et les longues dans un vers de n mātrās. Ce problème apparaît très tôt en Inde, sous le nom maatraameru (montagne de cadence), dans le travail du grammairien du sanskrit, Pingala, auteur du Chhandah-shastra (l'art de la Prosodie), vers 450 ou 200 av. J.-C. Le mathématicien indien Virahanka (en) en a donné des règles explicites au VIII^e siècle. Le philosophe indien Acharya Hemachandra (c. 1150) (et aussi Gopala, c. 1135) ont revisité le problème de manière assez détaillée^[3].

Si la syllabe longue L est deux fois plus longue que la syllabe courte C, les solutions sont, en fonction de la longueur totale de la cadence :

1 C → 1

2 CC,L → 2

3 CCC, CL, LC → 3

4 CCCC, CCL, CLC, LCC, LL → 5

5 CCCCC, CCCL, CCLC, CLCC, LCCC, CLL, LCL, LLC → 8

Le nombre de cadences fait apparaître les termes de la suite de Fibonacci. En effet, une cadence de longueur n peut être constituée en ajoutant C à une cadence de longueur n – 1, ou L à une cadence de longueur n – 2. Ainsi, le nombre de cadences de longueur n est la somme des deux nombres précédents de la suite.

Si on note S_n, le nombre de manière d'alterner les brèves et les longues dans un vers de n mātrās, cette remarque conduit naturellement à la relation de récurrence suivante : ${\displaystyle S_{n}=S_{n-1}+S_{n-2}}$, formule explicitement donnée dans l’œuvre de Virahanka^[4].

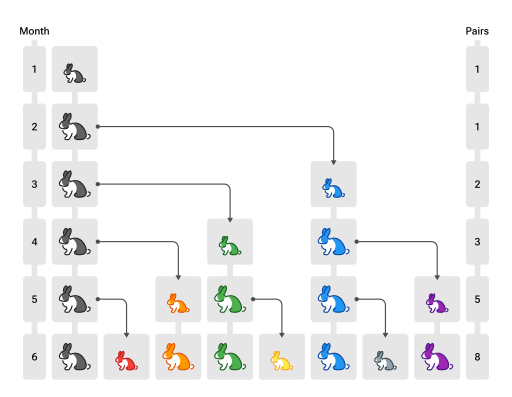
Population de lapins

La suite doit son nom à Leonardo Fibonacci qui, dans un problème récréatif posé dans l'ouvrage Liber abaci publié en 1202, décrit la croissance d'une population de lapins : « Quelqu’un a déposé un couple de lapins dans un certain lieu, clos de toutes parts, pour savoir combien de couples seraient issus de cette paire en une année, car il est dans leur nature de générer un autre couple en un seul mois, et qu’ils enfantent dans le second mois après leur naissance. »^[5]

Le problème de Fibonacci est à l'origine de la suite dont le n-ième terme correspond au nombre de paires de lapins au n-ième mois. Dans cette population idéale, on suppose que :

• au début du premier mois, il n'y a qu'une paire de lapereaux ;
• les lapins ne peuvent procréer qu'à partir de l'âge de deux mois ;
• chaque début de mois, toute paire susceptible de procréer engendre exactement une nouvelle paire de lapereaux ;
• les lapins ne meurent jamais (la suite de Fibonacci est donc croissante).

Notons F_n le nombre de couples de lapins au début du mois n. Jusqu’à la fin du deuxième mois, la population se limite à un couple ; on note F₁ = F₂ = 1.

Dès le début du troisième mois, le premier couple de lapins atteint l'âge de deux mois et engendre un second couple de lapins ; on note alors F₃ = 2.

Plaçons-nous maintenant au mois n et cherchons à exprimer ce qu'il en sera deux mois plus tard, soit au mois n + 2 : les F_{n + 2} couples de lapins sont formés des F_{n + 1} couples du mois précédent et des couples nouvellement engendrés.

Or, n'engendrent au mois n + 2 que les couples pubères, c'est-à-dire ceux qui existaient déjà deux mois auparavant, qui sont en nombre F_n. On a donc, pour tout entier n strictement positif :

${\displaystyle F_{n+2}=F_{n+1}+F_{n}}$.

On choisit alors de poser F₀ = 0, de manière que cette relation soit encore vérifiée pour n = 0.

On obtient ainsi la forme récurrente de la suite de Fibonacci : chaque terme de cette suite est la somme des deux termes précédents ; pour obtenir chacun de ces deux termes, il faut faire la somme de leurs termes précédents… et ainsi de suite, jusqu'à ce que ces deux termes soient les deux termes initiaux, F₁ et F₀, qui sont connus.

Expressions

Il existe plusieurs façons d'obtenir une expression mathématique du n-ième terme de la suite de Fibonacci.

Expression fonctionnelle

Le calcul du n-ième terme de la suite de Fibonacci via la formule de récurrence requiert le calcul des termes précédents. Au contraire, une expression fonctionnelle de la suite de Fibonacci est une expression où le calcul du n-ième terme ne présuppose pas la connaissance des termes précédents. Binet a redécouvert une formule en 1843^[6], qui avait déjà été obtenue par de Moivre^{[réf. nécessaire]} en 1718 et par Euler en 1765^[7]. Cette expression fonctionnelle s'appelle la formule de Binet :

(Ces calculs restent valables pour n entier négatif quand la suite est prolongée comme ci-dessous.)

Quand n tend vers +∞, F_n est équivalent à ${\displaystyle {\frac {\varphi ^{n}}{\sqrt {5}}}}$. Plus précisément, φⁿ tend vers l'infini et φ' ⁿ tend vers zéro car ${\displaystyle |\varphi '|<1<\varphi }$.

En fait, dès le rang n = 1, le deuxième terme ${\displaystyle {\varphi '^{n} \over {\sqrt {5}}}}$ est assez petit pour que les nombres de Fibonacci puissent être obtenus uniquement à partir du premier terme :

F_n est l'entier le plus proche de ${\displaystyle {\frac {\varphi ^{n}}{\sqrt {5}}}}$ (et il lui est supérieur ou inférieur, selon la parité de n).

Il existe d'autres démonstrations de la formule de Binet, telles que la transformation en Z et la technique des fonctions génératrices.^{[réf. nécessaire]}

Remarquons qu'une fois découverte, cette formule se démontre aussi par récurrence (y compris pour n entier négatif).

Expression matricielle

De la relation ${\displaystyle {\begin{bmatrix}F_{n}\\F_{n-1}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}{\begin{bmatrix}F_{n-1}\\F_{n-2}\end{bmatrix}}}$, on déduit ${\displaystyle {\begin{bmatrix}F_{n}\\F_{n-1}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}{\begin{bmatrix}0\\1\end{bmatrix}}}$ et ${\displaystyle {\begin{bmatrix}F_{n+1}\\F_{n}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}{\begin{bmatrix}1\\0\end{bmatrix}}}$; ceci permet d'écrire la forme matricielle :

En appliquant le déterminant, on obtient simplement l'identité de Cassini (propriété 5 ci-dessous) : ${\displaystyle F_{n+1}F_{n-1}-F_{n}^{2}=(-1)^{n}}$.

Et en calculant de deux façons ${\displaystyle {\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n+m}}$, on obtient (propriété 2 ci-dessous) : ${\displaystyle F_{n}F_{m+1}+F_{n-1}F_{m}=F_{n+m}}$.

Expression par déterminant d'ordre n - 1

En développant par rapport à la première colonne le déterminant d'ordre n :

${\displaystyle D_{n}={\begin{vmatrix}1&b&0&0&\cdots &0&0&0\\a&1&b&0&\cdots &0&0&0\\0&a&1&b&\cdots &0&0&0\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots \\0&0&0&0&\cdots &a&1&b\\0&0&0&0&\cdots &0&a&1\\\end{vmatrix}}}$, on obtient D_n = D_{n – 1} – abD_{n – 2} ; comme ${\displaystyle D_{1}=1,D_{2}=1-ab}$, si ab = –1, on obtient : D_n = F_{n + 1} d'où, pour ${\displaystyle n\geqslant 2}$:

Limite des quotients

Comme l'avait déjà remarqué Johannes Kepler^[8], le taux de croissance des nombres de Fibonacci, c'est-à-dire ${\displaystyle {\frac {F_{n+1}}{F_{n}}}}$, converge vers le nombre d'or φ.

En effet, puisque la suite F_n est équivalente à ${\displaystyle {\frac {\varphi ^{n}}{\sqrt {5}}}}$ (cf. supra, section Expression fonctionnelle), la suite ${\displaystyle {\frac {F_{n+1}}{F_{n}}}}$ est équivalente à ${\displaystyle {\frac {\frac {\varphi ^{n+1}}{\sqrt {5}}}{\frac {\varphi ^{n}}{\sqrt {5}}}}=\varphi }$, qui est donc sa limite.

En fait plus généralement, toutes les suites vérifiant la même relation de récurrence que la suite de Fibonacci (cf. infra, section Suites de Fibonacci généralisées) satisfont cette propriété, sauf celles commençant par a et aφ'.

Séries associées aux nombres de Fibonacci

Série des inverses

• La série des inverses des nombres de Fibonacci non nuls est convergente, et sa somme ${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{n}}}=3{,}35988566\dots }$ est parfois appelée constante de Fibonacci inverse ; Richard André-Jeannin en a démontré l'irrationalité^[9] en 1989^[10].
• La somme d'une de ses sous-séries ${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{F_{2^{k}}}}={\frac {7-{\sqrt {5}}}{2}}}$^[11],[12] est, elle, un nombre algébrique, voir la suite A079585 de l'OEIS.
• Le nombre ${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{F_{2^{k}+1}}}}$ est lui aussi irrationnel^[12], voir la suite  A338305.

Série des carrés des inverses

Il à été démontré que la somme ${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{(F_{n})^{2}}}=2{,}426323\dots }$ est un nombre transcendant, voir la suite A105393 de l'OEIS.

Bases et espaces vectoriels

• La dénomination de « suite de Fibonacci généralisée » est attribuée plus généralement à toute suite (G_n) définie sur ℕ vérifiant pour tout entier naturel n, G_{n + 2} = G_{n + 1} + G_n. Ces suites sont précisément celles pour lesquelles il existe des nombres a et b tels que pour tout entier naturel n, G_n = aF_n + bF_{n + 1}. Ainsi, l'ensemble des suites de Fibonacci est un sous-espace vectoriel de ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$et les suites (F_n) et (F_{n + 1}) en forment une base.
• Le nombre d'or est la racine positive du polynôme X² – X – 1, ainsi φ² = φ + 1. Si l'on multiplie les deux côtés par φⁿ, on obtient φ^{n + 2} = φ^{n + 1} + φⁿ, donc la suite (φⁿ) est une suite de Fibonacci. La racine négative du polynôme, φ' = 1 – φ, possède les mêmes propriétés, et les deux suites linéairement indépendantes (φⁿ) et (φ'ⁿ), forment une autre base de l'espace vectoriel.

Interprétations combinatoires

Dénombrements de compositions

F_n+1 est égal au nombre de suites finies d'entiers égaux à 1 ou 2 dont la somme est égale à n (ou compositions de n formées des entiers 1 ou 2) ^[13]. Par exemple ${\displaystyle F_{4}=3}$ car ${\displaystyle 3=1+1+1=1+2=2+1}$. On peut donc interpréter F_n+1 comme :

• le nombre de façons différentes de paver un rectangle 2×n au moyen de dominos 2×1,
• le nombre de façons de vider un tonneau de n litres à l'aide de bouteilles de un ou deux litres.

Démonstration : les compositions de n se terminant par 1 sont obtenues en ajoutant 1 à la fin d'une composition de ${\displaystyle n-1}$, celles se terminant par 2 sont obtenues en ajoutant 2 à la fin d'une composition de ${\displaystyle n-2}$, donc le nombre ${\displaystyle C_{n}}$ de compositions de n vérifie ${\displaystyle C_{n}=C_{n-1}+C_{n-2}}$. De plus, ${\displaystyle C_{0}=F_{1}=1}$ (la composition vide), ${\displaystyle C_{1}=F_{2}=1}$ (la composition (1)), ce qui montre la relation.

Dénombrements de suites de pile ou face

F_n+2 est égal au nombre de jeux de pile ou face de longueur n qui ne contiennent pas 2 "pile" consécutifs.

Démonstration : pour former un jeu de longueur n qui ne contient pas 2 "pile" consécutifs on peut commencer par 0, et continuer avec un jeu de longueur n – 1 du même type, soit commencer par 1, 0 et continuer avec un jeu de longueur n – 2 du même type, donc le nombre ${\displaystyle P_{n}}$ de tels jeux vérifie ${\displaystyle P_{n}=P_{n-1}+P_{n-2}}$ ; De plus, ${\displaystyle P_{0}=F_{2}=1}$ ( jeu de longueur nulle), ${\displaystyle P_{1}=F_{3}=2}$ ((1) et (0)), ce qui montre la relation.

On en déduit que F_n+2 est aussi le nombre de parties de ${\displaystyle [\![1,n]\!]}$ ne contenant pas 2 entiers consécutifs.

Algorithmes de calcul des nombres de Fibonacci

Le calcul des nombres de Fibonacci est souvent donné en exemple pour introduire des notions d'algorithmique, comme dans le chapitre 0 du livre Algorithms de Dasgupta et al.^[14] ou alors dans le problème 31.3 laissé en exercice dans Introduction à l'algorithmique de Cormen et al.^[15] ou l'exercice 2 de la section 1.2.8 de TAOCP, qui est précisément consacrée aux nombres de Fibonacci.

Avec la formule de Binet

Calculer les nombres de Fibonacci à partir du nombre d'or est une possibilité très pratique. Néanmoins, la précision de calcul de la racine carrée génère des erreurs d'arrondis pour des valeurs assez grandes dépendant du système utilisé^[16]. En général, on obtient les bonnes valeurs jusqu’à F₇₁ = 308 061 521 170 129, sur ordinateur ou sur calculatrice.

Notons^{[réf. nécessaire]} qu’au-delà de F₇₉, les calculs dépassent les possibilités de calcul en notation entière, et sont alors représentés en notation scientifique. Les premiers chiffres significatifs sont alors de nouveau bien représentés par cette formule.

Voici le détail d’un exemple d'application faisable à partir d'une calculatrice : le calcul de F₅₀.

Le nombre d’or vaut ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618}$ et d'après la formule de Binet, ${\displaystyle F_{50}}$ est l'entier le plus proche du réel ${\displaystyle {\frac {\varphi ^{50}}{\sqrt {5}}}}$, qui le dépasse à peine. Compte tenu de l'ordre de grandeur de ce réel, le théorème des accroissements finis permet de s'assurer que pour le calculer à 0,5 près par défaut, 1,618 033 988 749 89 est une approximation suffisante de φ.

On trouve que le réel (1,618 033 988 749 89)⁵⁰/√5 est à peine inférieur à l'entier 12 586 269 025, d'où

${\displaystyle F_{50}\approx {\frac {\varphi ^{50}}{\sqrt {5}}}\approx 12\,586\,269\,025}$,

si bien que

${\displaystyle F_{50}=12\,586\,269\,025}$.

Algorithme récursif naïf

Voici la mise en œuvre récursive naïve qui suit la définition de la suite de Fibonacci.

// entrée : un nombre entier n
// sortie : le terme de rang n de la suite de Fibonacci
fonction fib(n)
    si n = 0
        renvoyer 0
    sinon si n = 1
        renvoyer 1
    sinon
        renvoyer fib(n - 1) + fib(n - 2)

Ce n'est cependant pas une façon judicieuse de calculer la suite de Fibonacci, car on calcule de nombreuses fois les mêmes valeurs. Le temps de calcul est exponentiel en n, à moins d'employer une technique de mémoïsation.

Algorithme polynomial

On calcule le n-ième terme de la suite de Fibonacci en mémorisant deux termes consécutifs de la suite. On commence avec les deux premières valeurs a = 0 et b = 1, puis on remplace répétitivement le premier nombre par le second, et le second nombre par la somme des deux.

fonction fib(n)
    (a, b) ← (0, 1)
    pour i de 1 à n
        (a, b) ← (b, a + b)
    renvoyer a

L'algorithme réalise n additions. On peut montrer que le n-ième terme de la suite de Fibonacci s'écrit avec O(n) bits. Comme l'addition de deux nombres sur n bits est linéaire en n, l'algorithme est en O(n²)^[14]. De manière équivalente à l'algorithme ci-dessus, on peut écrire une fonction récursive terminale, c'est-à-dire où la dernière opération effectuée par la fonction est un appel récursif. Voici un algorithme récursif terminal^[17] pour calculer la suite de Fibonacci.

fonction fib(n, a, b)
    si n = 0
        renvoyer a
    sinon si n = 1
        renvoyer b
    sinon
        renvoyer fib(n - 1, b, a + b)

L'appel à fib(n, 0, 1) lance le calcul pour la valeur de n donnée. Les paramètres a et b sont des accumulateurs : la valeur de a est F_n et celle de b est F_{n + 1}. Le temps de calcul est à chaque fois proportionnel à n. Par contre, l'espace mémoire occupé n'est a priori plus constant. Pour les langages qui réalisent l'optimisation d'élimination de la récursivité terminale, la mémoire occupée est constante.

Algorithme corécursif

En Haskell, on peut définir la suite de Fibonacci comme un stream (une liste infinie qui est évaluée de façon paresseuse^[18])^[19].

fibs = 0:1:zipWith (+) fibs (tail fibs)

Le calcul du n-ième terme s'effectue avec :

fibs !! n

Algorithme avec expression matricielle

Comme vu ci-dessus,${\displaystyle {\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}={\begin{bmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{bmatrix}}}$, on écrit un algorithme qui utilise l'exponentiation rapide pour calculer ${\displaystyle {\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}}$, afin d'en déduire le n-ième terme. Si on considère les additions et multiplications de nombres comme des opérations élémentaires, en coût constant, l'algorithme est logarithmique en n. En comptabilisant la complexité des additions et multiplications, on peut montrer que la complexité de cet algorithme est en O(M(n) log n), et même O(M(n)), où M(n) est la complexité de l'algorithme utilisée pour réaliser une multiplication de deux nombres sur n bits (voir exercice 0.4 dans ^[14]).

Série génératrice

La série génératrice de la suite de Fibonacci^[20] donne une série entière dont le rayon de convergence vaut 1/φ (d'après le théorème de Cauchy-Hadamard ou plus simplement, la règle de d'Alembert). Pour tout complexe z de module strictement inférieur à 1/φ, la série correspondante (absolument convergente) est égale à ${\displaystyle \sum _{n\in \mathbb {N} }F_{n}z^{n}={\frac {z}{1-z-z^{2}}}}$ (donc à ${\displaystyle z\sum _{m\in \mathbb {N} }(z+z^{2})^{m}=\sum _{m,k\in \mathbb {N} }{m \choose k}z^{1+m+k}}$, où les coefficients binomiaux ${\displaystyle m \choose k}$ sont nuls pour k > m).

En particulier, pour tout réel k > φ, ${\displaystyle {\frac {1}{k^{2}-k-1}}=\sum _{n=1}^{\infty }F_{n}\times k^{-(n+1)}}$.

Propriétés de la suite de Fibonacci

La suite de Fibonacci présente de remarquables propriétés. Leur recherche et leur étude font l'objet de publications régulières, notamment par l'association d'universitaires « The Fibonacci Association » dans sa revue « The Fibonacci Quarterly », consultable en ligne^[21]. Certaines de ces propriétés, que l'on peut démontrer à partir de la formule de Binet, ou par récurrence ou encore à l'aide de l'expression matricielle de la suite, sont indiquées dans cette section. Nous donnons également quelques propriétés liant la suite de Fibonacci et la suite de Lucas (L_n ) définie par la même relation de récurrence mais avec pour initialisation L₀ = 2 et L₁ = 1, et pour laquelle l'analogue de la formule de Binet est : ${\displaystyle L_{n}=\varphi ^{n}+\varphi '^{n}}$.

Propriété 1 : ${\displaystyle \forall (p,q,r)\in \mathbb {Z} ^{3},F_{p}F_{q+r}-(-1)^{r}F_{p-r}F_{q}=F_{p+q}F_{r}}$, ou encore : ${\displaystyle F_{p}F_{q+r}-F_{r}F_{p+q}=(-1)^{r}F_{p-r}F_{q}}$.

C'est un cas particulier des identités remarquables vérifiées par les suites récurrentes linéaires d'ordre 2

Propriété 2 : ${\displaystyle \forall (p,q)\in \mathbb {Z} ^{2},F_{p}F_{q+1}+F_{p-1}F_{q}=F_{p+q}}$.

C'est le cas r = 1 de la propriété 1^[22]. On peut aussi la démontrer à l'aide de l'expression matricielle :

Propriété 3 : ${\displaystyle \forall p\in \mathbb {Z} ,F_{2p-1}=F_{p-1}^{2}+F_{p}^{2}}$.

C'est le cas q = p – 1 de la propriété 2.

Propriété 4 : (identité d'Ocagne)${\displaystyle \forall (p,r)\in \mathbb {Z} ^{2},F_{p}F_{r+1}-F_{r}F_{p+1}=(-1)^{r}F_{p-r}}$.

C'est le cas q = 1 de la propriété 1.

Propriété 5 : ${\displaystyle \forall (p,q)\in \mathbb {Z} ^{2},F_{p}^{2}-F_{p-q}F_{p+q}=(-1)^{p-q}F_{q}^{2}}$ (identité de Catalan) et ${\displaystyle F_{p+1}F_{p-1}-F_{p}^{2}=(-1)^{p}}$ (identité de Cassini^[13],[23]).

L'identité de Catalan est le cas r = p – q de la propriété 1. L'identité de Cassini est le cas q = 1 de celle de Catalan (c'est donc aussi le cas r = p – 1 de la propriété 4). L'identité de Cassini peut aussi se démontrer à l'aide de l'expression matricielle :

Corollaire 1 : ${\displaystyle \forall p\in \mathbb {Z} ,F_{p}={\frac {F_{p-1}+{\sqrt {5F_{p-1}^{2}-4(-1)^{p}}}}{2}}~{\text{et}}~{\sqrt {5F_{p}^{2}+4(-1)^{p}}}\in \mathbb {N} }$.

Corollaire 2 : ${\displaystyle \forall p\in \mathbb {Z} ,F_{p+2}F_{p+1}F_{p-1}F_{p-2}-F_{p}^{4}+1=0}$.

Propriété 6 : La suite de Fibonacci est à divisibilité faible^[24] : ${\displaystyle \forall (k,n)\in \mathbb {Z} ^{2}\quad F_{n}\mid F_{nk}}$^[25].

Cela résulte de la propriété 2.

On peut aussi démontrer cette propriété par la proposition 4 (par récurrence sur |k|), ou par un calcul explicite du quotient (en particulier, ${\displaystyle F_{2n}=F_{n}L_{n}}$).

Propriété 7 : Pour tout entier naturel n différent de 4, si F_n est premier, alors n est premier.

La réciproque est fausse, car 2 est premier alors que F₂ ne l'est pas ; de façon moins triviale, ${\displaystyle F_{19}=4181=37\times 113}$.

Propriété 8 : La suite de Fibonacci est même à divisibilité forte^[26] : ${\displaystyle \forall (a,b)\in \mathbb {Z} \times \mathbb {Z} ^{*},~F_{a}\land F_{b}=F_{a\land b}}$, où ∧ désigne le PGCD de nombres entiers.

En particulier pour tout entier n, F_n et F_{n + 1} sont premiers entre eux^[27].

Propriété 9 : ${\displaystyle \forall (p,r)\in \mathbb {Z} ^{2},F_{p+r}-(-1)^{r}F_{p-r}=F_{r}L_{p}}$. En particulier :

${\displaystyle F_{p+1}+F_{p-1}=L_{p},\quad F_{p+2}-F_{p-2}=L_{p},\quad F_{p+3}+F_{p-3}=2L_{p}}$.

L'égalité est immédiate si p = 0. Pour p ≠ 0, c'est le cas particulier q = p de la propriété 1.

Propriété 10 : ${\displaystyle \forall n\in \mathbb {Z} ,\varphi ^{n}=F_{n}\varphi +F_{n-1}~{\text{et}}~\varphi '^{n}=F_{n}\varphi '+F_{n-1}}$.

Propriété 11 : La suite de Fibonacci possède plusieurs propriétés de récurrence additive forte, notamment : ${\displaystyle \forall n\in \mathbb {N} ^{*}\quad \sum _{i=1}^{n}F_{2i-1}=F_{2n},\quad 1+\sum _{i=0}^{n-1}F_{2i}=F_{2n-1}\quad {\text{et}}\quad 1+\sum _{i=0}^{n-1}F_{i}=F_{n+1}}$^[28].

La suite ${\displaystyle (F_{2n})}$ vérifie en outre : ${\displaystyle F_{2n}=n+\sum _{k=1}^{n-1}(n-k)F_{2k}}$ pour ${\displaystyle n\geqslant 2}$ ; voir la suite A088305 de l'OEIS.

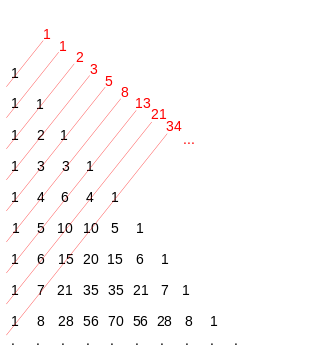
Propriété 12 : ${\displaystyle \forall n\in \mathbb {N} ,~F_{n}=\sum _{k\in \mathbb {Z} }{n-1-k \choose k}}$ (somme finie car les coefficients binomiaux ${\displaystyle {n-1-k \choose k}}$ sont nuls si k < 0 ou si k > n – 1 – k).

Cette propriété se déduit immédiatement de l'expression de la série génératrice (voir supra). On peut aussi la démontrer par une récurrence d'ordre 2 sur n^[22] :

Cela signifie que, dans un triangle de Pascal, les nombres de Fibonacci s'obtiennent en sommant les termes situés sur une diagonale (du bas vers la droite). Les termes de ces diagonales sont d'ailleurs les coefficients des polynômes de Fibonacci ; ainsi, ${\displaystyle F_{6}(x)=x^{5}+4x^{3}+3x}$ et ${\displaystyle F_{9}(x)=x^{8}+7x^{6}+15x^{4}+10x^{2}+1}$.

Propriété 13 : ${\displaystyle \forall n\in \mathbb {N} ,~2^{n-1}F_{n}=\sum _{0\leq k\leq n/2}{n \choose 2k+1}5^{k}}$.

Cette propriété découle du développement binomial de la formule de Binet^[29] ; on a d'ailleurs une formule analogue pour les nombres de Lucas : ${\displaystyle \forall n\in \mathbb {N} ,~2^{n-1}L_{n}=\sum _{0\leq k\leq n/2}{n \choose 2k}5^{k}}$.

Propriété 14 : La suite ${\displaystyle (u_{n})_{n\in \mathbb {N} ^{*}}}$ définie par ${\displaystyle u_{n}=F_{n+1}/F_{n}}$ vérifie${\displaystyle u_{n+1}=1+1/u_{n}{\text{ et }}u_{n}^{2}-u_{n}-1=(-1)^{n}/F_{n}^{2}}$.

Propriété 15 : La factorisation des polynômes de Fibonacci permet d'exprimer les ${\displaystyle {F}_{n}}$ (pour n ≥ 1) sous forme de produits trigonométriques^[30] :${\displaystyle {F}_{n}=\prod _{1\leq k\leq (n-1)/2}3+2\cos \left({\frac {2k\pi }{n}}\right)}$.

Arithmétique

Divisibilité des nombres de Fibonacci

Une première approche de la question de la divisibilité de F_n par un entier a consiste à étudier la suite des restes de F_n modulo a : cette suite (r_n) vérifie (dans Z/aZ) la même récurrence (r_n+2 = r_n+1 + r_n) et est donc périodique de période au plus a² (les longueurs des périodes en fonction de a forment la suite des périodes de Pisano, suite A001175 de l'OEIS) ; on en déduit que pour tout a, il existe n inférieur ou égal à a² tel que F_n (et donc F_kn) soit divisible par a. Plus précisément, l'étude de cette récurrence dans le corps Z/pZ (où p est un nombre premier) amène à des formules analogues à la formule de Binet, d'où l'on déduit finalement (selon que 5 est ou n'est pas un carré modulo p ; voir la loi de réciprocité quadratique) que ${\displaystyle F_{5n}}$ est divisible par 5, et que si p est premier autre que 5, ${\displaystyle F_{(p-1)n}}$ est divisible par p si p est de la forme 5m + 1 ou 5m + 4, et ${\displaystyle F_{(p+1)n}}$ est divisible par p sinon. Des résultats plus précis peuvent d'ailleurs être obtenus ; ainsi, dans le premier cas, ${\displaystyle F_{(p-1)/2}}$ est divisible par p si (p – 1)/2 est pair^[31]. Enfin, si p > 2 est premier et divise F_n, p^k divise ${\displaystyle F_{p^{k-1}n}}$, et 2^k+1 divise ${\displaystyle F_{3\times 2^{k-1}}}$ (si k>1) ; ces derniers résultats sont des conséquences du lemme de Hensel^[32],[33] ; les mêmes méthodes permettent d'obtenir des résultats analogues pour les nombres de Lucas^[31],[34].

Primalité des nombres de Fibonacci

Un nombre premier de Fibonacci est un nombre de Fibonacci qui est également premier.

Les sept plus petits nombres premiers de Fibonacci ${\displaystyle F_{n}}$ sont^[35] 2, 3, 5, 13, 89, 233 et 1 597, et les indices n correspondants sont 3, 4, 5, 7, 11, 13 et 17 (sauf pour ${\displaystyle F_{4}}$, ces indices sont nécessairement premiers^[36]) .

On découvre au fil des ans des nombres de Fibonacci premiers de plus en plus grands, mais on ignore toujours s'il en existe une infinité.

Décomposition d'un entier en somme de nombres de Fibonacci

Tout entier positif se décompose de manière unique en la somme de nombres de Fibonacci d'indice supérieur ou égal à 2, les indices successifs de ces nombres ayant une différence supérieure ou égale à 2 lorsqu'ils sont rangés dans l'ordre.

Exemple

${\displaystyle 25=21+3+1=F_{8}+F_{4}+F_{2}}$.

Applications

En mathématiques

• La suite de Fibonacci apparaît dans de nombreux problèmes de dénombrement. Par exemple, le terme d'indice n (pour n supérieur ou égal à 2) de la suite de Fibonacci permet de dénombrer le nombre de façons de parcourir un chemin de longueur n-1 en faisant des pas de 1 ou 2. Ce problème est également équivalent au problème de bin packing pour n articles de longueur 1 ou 2, tel qu'on le trouve par exemple dans The Art of Computer Programming de Donald Knuth.^{[réf. nécessaire]}
• Les nombres de Fibonacci interviennent dans l'étude de l'exécution de l'algorithme d'Euclide qui détermine le plus grand commun diviseur de deux entiers^[15].
• Ils sont l'outil (grâce à la propriété 8 et la factorisation de F₁₉) d'une démonstration originale du théorème d'Euclide sur les nombres premiers^[37].
• Youri Matiiassevitch a montré que les nombres de Fibonacci pouvaient être définis par une équation diophantienne^{[réf. nécessaire]}, ce qui a conduit à la résolution du dixième problème de Hilbert. En 1975, Jones en a déduit que, pour des valeurs de x et y entières positives ou nulles, les valeurs positives du polynôme ${\displaystyle 2xy^{4}+x^{2}y^{3}-2x^{3}y^{2}-y^{5}-x^{4}y+2y}$ étaient exactement les nombres de Fibonacci^{[réf. nécessaire]}. Ces valeurs positives s'obtiennent d'ailleurs en attribuant pour valeurs à x et y deux nombres de Fibonacci successifs.
• Les nombres de Fibonacci apparaissent dans la formule des diagonales du triangle de Pascal (voir Propriétés, Propriété 12).

• Une bonne approximation d'un rectangle d'or peut être construite à l'aide de carrés dont les côtés sont égaux aux nombres de Fibonacci.

  

• Une spirale logarithmique peut être approchée de la manière suivante : on commence à l'origine d'un repère cartésien, on se déplace de F₁ unités vers la droite, puis de F₂ unités vers le haut, on se déplace de F₃ unités vers la gauche, ensuite de F₄ unités vers le bas, puis de F₅ unités vers la droite, etc. Cela ressemble à la construction mentionnée dans l'article sur le nombre d'or.
• Les nombres de Fibonacci apparaissent souvent dans la nature lorsque des spirales logarithmiques sont construites à partir d'une unité discrète, telles que dans les tournesols ou dans les pommes de pin. Le nombre de pétales de la marguerite (et d'autres fleurs composées comme le tournesol) appartient à la suite de Fibonacci : souvent 34, 55 ou 89. Cela s'explique par le mécanisme de développement de la plante (voir le paragraphe « Phyllotaxie » de l'article sur le nombre d'or).

Informatique

• La suite de Fibonacci est utilisé comme outil mathématique dans l'analyse de la complexité pire cas de l'algorithme du simplexe^[38].
• La suite de Fibonacci intervient dans les tas de Fibonacci.

Biologie

La plupart des êtres vivants sexués sont issus de deux parents, de sorte que leurs ancêtres à la n^e génération, supposés distincts, sont au nombre de 2ⁿ. Mais les hyménoptères sont tels que les femelles sont issues de deux parents, et les mâles sont issus d'une mère seulement. Il en résulte que leurs ancêtres à la n-ième génération sont constitués :pour les femelles, de F_n mâles et F_{n + 1} femelles,pour les mâles, de F_{n – 1} mâles et F_n femelles. Cette forme de reproduction asexuée décrit exactement la reproduction des abeilles. Récemment, une analyse mathématique et historique du contexte de Fibonacci et sa proximité de la ville de Béjaïa, une grande source de cire à l'époque (la version française du nom de cette ville est Bougie), a suggéré que ce seraient en fait les apiculteurs de Béjaïa et la connaissance de la reproduction des abeilles qui, plutôt que la reproduction des lapins, auraient inspiré la découverte de Fibonacci^[39].

Art

En poésie, un fib est un petit poème, sorte de haïku, dont le nombre de pieds des premiers vers correspond aux premiers nombres de la suite (1, 1, 2, 3, 5, 8).

Généralisations

Il existe plusieurs façons de généraliser la suite de Fibonacci : étendre aux indices négatifs, modifier les valeurs initiales, modifier les coefficients de la relation de récurrence ou modifier le nombre de termes (ou ordre) de la relation de récurrence. Si on modifie tout à la fois (initialisation, récurrence, ordre) on arrive à l'ensemble général des suites à récurrence linéaire. Un bon nombre de propriétés se généralisent au cas où le polynôme minimal de la suite récurrente linéaire définit un nombre de Pisot. Ces propriétés ont été étudiées en lien avec la théorie des automates finis (sur les mots finis et les mots infinis) dans la thèse d'État de Christiane Frougny sur la représentation des entiers et des réels en base Pisot, sur une suggestion de Marcel-Paul Schützenberger.

Extension aux indices négatifs

La suite est étendue aux indices négatifs et Knuth parle de nombres de negafibonacci^[40]. La formule de récurrence les définit aussi de proche en proche :${\displaystyle F_{n}=F_{n+2}-F_{n+1}}$

Ainsi, autour de 0, la suite est :

F–6

F–5

F–4

F–3

F–2

F–1

F0

F1

F2

F3

F4

F5

F6

−8

5

−3

2

−1

1

0

1

1

2

3

5

8

On remarque, sur ces premières valeurs, que

• si n est pair alors F_–n = –F_n
• si n est impair alors F_–n = F_n

ou plus synthétiquement :

${\displaystyle F_{-n}=(-1)^{n+1}F_{n}}$.

On peut le démontrer pour tout entier n, par la formule de Binet ci-dessus, ou directement par récurrence.

Suites de Fibonacci généralisées

On appelle suite de Fibonacci généralisée toute suite définie par la même relation de récurrence que la suite de Fibonacci, mais dont les termes initiaux sont différents de 0 et 1^{[réf. nécessaire]}. Sur le modèle de la démonstration donnée plus haut (voir section Expression fonctionnelle), une telle suite u_n) est encore de la forme αφⁿ + βφ'ⁿ où φ est le nombre d'or et ${\displaystyle \varphi '=-1/\varphi }$. Elle est donc équivalente à αφⁿ, sauf si α = 0 (ce qui ne se produit que si ${\displaystyle u_{1}=\varphi 'u_{0}}$), si bien que (comme la suite des quotients de la suite de Fibonacci) la suite ${\displaystyle {\frac {u_{n+1}}{u_{n}}}}$ converge vers φ.

Parmi ces suites de nombres, il faut signaler les nombres de Lucas obtenus en choisissant comme initialisation : ${\displaystyle L_{0}=2}$ et ${\displaystyle L_{1}=1}$. Cela donne la suite 2, 1, 3, 4, 7, 11, 18, 29,… On trouve parfois une initialisation ${\displaystyle L_{0}=1}$ et ${\displaystyle L_{1}=3}$ qui ne consiste qu'à décaler la suite d'un rang. Ces nombres interviennent dans la résolution d'équations diophantiennes. Ils sont très liés à la suite de Fibonacci par la relation suivante : ${\displaystyle L_{n}=F_{n+1}+F_{n-1}}$ pour tout entier n > 0 (voir Propriétés, Propriété 9).

Suites de Lucas

Ce sont les suites où la relation de récurrence a changé et est est devenue^{[réf. nécessaire]}

${\displaystyle X_{n+2}=PX_{n}-QX_{n+1}}$.

Elles sont de deux types, notés X = U et X = V, selon que l'initialisation est U₀ = 0 et U₁ = 1 ou qu'elle est V₀ = 2 et V₁ = P.

La suite de Fibonacci et la suite des nombres de Lucas sont les suites U et V de Lucas de paramètres P = 1 et Q = –1.

Suites de k-bonacci

Ce sont des suites dont la relation de récurrence est d'ordre ${\displaystyle k}$^[41]. Un terme est la somme des ${\displaystyle k}$ termes qui le précèdent :

${\displaystyle u_{n+k}\,=\,u_{n}+u_{n+1}+u_{n+2}+\dots +u_{n+k-1}}$.

Parmi ces suites, on distingue la suite de Tribonacci (récurrence d'ordre 3) et la suite de Tetranacci (récurrence d'ordre 4). Selon ce nouveau classement de suites, la suite de Fibonacci est une suite de 2-bonacci.

Dans la nature

La suite de Fibonacci apparaît sous de nombreuses formes biologiques^[42], comme la ramification des arbres, la disposition des feuilles sur une tige, les fruits de l'ananas^[43], la floraison de l'artichaut, le déroulement des feuilles de fougères, la disposition d'une pomme de pin^[44], la coquille de l’escargot et la disposition des nuages lors des ouragans. Quant aux marguerites, elles ont le plus souvent un nombre de pétales issu de la suite de Fibonacci.

Chez les Astéracées, dans les inflorescences en capitule, la disposition des fleurons sur le réceptacle forme des spirales régulières, dextres et sénestres, qui suivent les règles de la phyllotaxie dans lesquelles on peut retrouver la suite de Fibonacci^[43].

Les abeilles domestiques ont une reproduction haplodiploïde : un œuf non fécondé donnera un mâle et un œuf fécondé donnera une ouvrière ou une reine. Ainsi, un mâle aura une mère, quand les ouvrières et reine auront une mère et un père. Par conséquent, le pedigree d'un mâle est constitué d'un parent, de deux grands-parents, de trois arrière-grands-parents, de cinq arrière-arrière-grands-parents, etc. ; il s'agit d'une suite de Fibonacci^[45].

Dans la culture

Peinture

Dans son tableau Parade de cirque, peint en 1887-1888, Georges Seurat emploie les premiers termes de la suite : un personnage central, deux personnages à droite, trois musiciens, cinq banderoles ou cinq spectateurs en bas à gauche, huit à droite, treize en tout^[46].

Littérature

Cinéma

Télévision

Musique

• Le groupe de metal progressif Tool structure le rythme de certaines parties du morceau Lateralus selon une suite de Fibonacci^[50].
• La chanteuse suisse pour enfants Sonia Grimm a publié sur son album Un petit lapin une chanson intitulée Le lapin de Fibonacci. Cette chanson présente aux enfants le nombre d'or et la suite de Fibonacci à travers l'exemple de la croissance d'une population de lapins^[51].
• Selon Ernő Lendvaï^[52], le compositeur Béla Bartók s'est régulièrement servi du nombre d'or et de la suite de Fibonacci dans ses œuvres. L'exemple le plus emblématique serait sa Musique pour cordes, percussion et célesta. Cependant, d'autres spécialistes de Bartók ont critiqué cette interprétation^[53].
• Le compositeur Iannis Xenakis a plusieurs fois utilisé la suite de Fibonacci : dès 1952 en tentant de créer une "image auditive" de cette série, puis dans quelques compositions : Zygia en 1952 et Le Sacrifice en 1953^[54].
• Sur la guitare de Robert Smith, chanteur de The Cure, pour la tournée 2016 du groupe, figure le début de la suite de Fibonacci^[55].

Architecture

Le Corbusier et son Modulor, une mesure harmonique à l'échelle humaine applicable universellement à l'architecture et à la mécanique.

• Illustrations architecturales
• 
  Cheminée d'usine à Unna.
• 
  Mole Antonelliana à Turin.

Mario Merz, Suite de Fibonacci, commande publique artistique, 1994, Strasbourg.

Jeux et jeux vidéo

Dans le jeu Metal Gear Solid 4: Guns of the Patriots, la suite de Fibonacci apparaît en tant que petite comptine chantée par la petite Sunny.

Dans le jeu Watch Dogs, la suite de Fibonacci est introduite dans l'algorithme de Bellwether, capable de transmettre un message subliminal à travers le système ctOS.

Dans le jeu Elite sur BBC Micro, les développeurs ont utilisé la suite de Fibonacci pour permettre au jeu de tenir dans 22 ko. Le jeu génère donc aléatoirement la galaxie, mais il peut ensuite la générer exactement de la même façon lorsqu'une partie est sauvegardée puis rechargée.

Le jeu de société « 4.6.Suite » (jeu de cartes) est basé sur les suites numériques et notamment sur les suites de Fibonacci.

Informatique

En méthodologie scrum, la suite de Fibonacci est utilisée pour chiffrer les développements lors du planning poker.^{[réf. nécessaire]}

Curiosité

La suite de Fibonacci peut servir à mémoriser des conversions de milles américains en kilomètres^{[réf. nécessaire]}. En effet, 1 mi = 1,609 km, or le nombre d'or φ ≈ 1,6 et F_{n + 1} ≈ φF_n donc on peut utiliser la formule approchée : F_n mi ≈ F_{n + 1} km, éventuellement multipliée par une constante^{[Laquelle ?]}.

Par exemple, 3 mi ≈ 5 km (en réalité 4,8 km), donc 6 mi ≈ 10 km, 5 mi ≈ 8 km donc 10 mi ≈ 16 km et 50 mi ≈ 80 km, 8 mi ≈ 13 km.

Notes et références

Voir aussi

Bibliographie

• (en) Hrant Arakelian, Mathematics and History of the Golden Section, Logos 2014, 404 p. (ISBN 978-5-98704-663-0) (rus.)
• (en) J. H. Halton, « On the divisibility properties of Fibonacci numbers », Fibonacci Quarterly, vol. 4, n^o 3,‎ 1966, p. 217-240 (lire en ligne)
• Nikolai Vorobiev (en), Caractères de divisibilité — Suite de Fibonacci, coll. Initiation aux Mathématiques, Éditions Mir, Moscou, 1973
• Ronald Graham, Donald Knuth et Oren Patashnik (trad. Alain Denise), Mathématiques concrètes : Fondations pour l'informatique, Paris, Vuibert, 2003, 2^e éd., xiv+688 (ISBN 978-2-7117-4824-2), § 6.6 p. 309.

Articles connexes

• Généralisations de la suite de Fibonacci
• Groupe de Fibonacci
• Mot de Fibonacci
• Codage de Fibonacci
• The Fibonacci Association

Liens externes

• (en) Eric W. Weisstein, « Fibonacci Sequence », sur MathWorld
• (en) Eric W. Weisstein, « Fibonacci Q-Matrix », sur MathWorld
• Suite de Fibonacci et nombre d'or dans l'ensemble de Mandelbrot
• Suite de Fibonacci dans le dictionnaire des nombres
• J.-C. Michel, « Le nombre d'or », sur gecif.net
• (en) R. N. Knott et the Plus Team, « The life and numbers of Fibonacci », sur plus.maths.org, 4 novembre 2013
• Benoît Rittaud, « Les suites de Fibonacci aléatoires », sur Daylymotion, Universcience
• Notices d'autorité :

  • BnF (données)
  • LCCN
  • Israël
  • Tchéquie

• Portail de l'analyse
• Portail des mathématiques

wikifunctions:Z13835