Filtre adaptatif

Un filtre adaptatif est un système avec un filtre linéaire dont la fonction de transfert est contrôlée par des paramètres variables et un moyen d'ajuster ces paramètres selon un algorithme d'optimisation. En raison de la complexité des algorithmes d'optimisation, presque tous les filtres adaptatifs sont des filtres numériques. Les filtres adaptatifs sont nécessaires pour certaines applications parce que certains paramètres du traitement souhaité (par exemple, l'emplacement des surfaces réfléchissantes dans un espace réverbérant) ne sont pas connus à l'avance ou changent. Le filtre adaptatif en boucle fermée utilise une rétroaction sous la forme d'un signal d'erreur pour affiner sa fonction de transfert.

De manière générale, le processus adaptatif en boucle fermée implique l'utilisation d'une fonction objectif, qui est un critère de performance optimale du filtre, pour alimenter un algorithme, qui détermine comment modifier la fonction de transfert du filtre pour minimiser le coût à l'itération suivante. La fonction de coût la plus courante est le carré moyen du signal d'erreur.

Avec l'augmentation de la puissance des processeurs de signal numérique (DSP), les filtres adaptatifs sont devenus beaucoup plus courants et sont maintenant utilisés couramment dans des appareils tels que les téléphones mobiles et autres appareils de communication, les caméscopes et les appareils photo numériques, ainsi que les équipements de surveillance médicale.

Exemple d'application

L'enregistrement d'un battement de cœur (par électrocardiographie ou ECG) peut être corrompu par le bruit provenant de l'alimentation électrique (secteur). La fréquence exacte du courant et de ses harmoniques peut varier dans le temps.

Une façon d'éliminer le bruit consiste à filtrer le signal à l'aide d'un filtre coupe-bande à la fréquence du secteur et à ses environs, mais cela pourrait dégrader excessivement la qualité de l'ECG puisque le battement du cœur aurait probablement aussi des composantes de fréquence dans la plage rejetée.

Pour contourner cette perte potentielle d'informations, un filtre adaptatif peut être utilisé. Le filtre adaptatif prendrait en entrée à la fois le signal provenant de la sonde du patient et celui du secteur et serait donc capable de suivre la fréquence réelle du bruit lorsqu'il fluctue et de soustraire ce bruit de l'enregistrement. Une telle technique adaptative permet généralement d'obtenir un filtre avec une plage de réjection plus petite, ce qui signifie, dans ce cas, que la qualité du signal de sortie est plus précise à des fins médicales^[1],[2].

Schéma fonctionnel

L'idée derrière un filtre adaptatif en boucle fermée est qu'un filtre variable est ajusté jusqu'à ce que l'erreur (la différence entre la sortie du filtre et le signal désiré) soit minimisée. Le filtre des moindres carrés (en) (LMS) et le filtre des moindres carrés récursifs (RLS) sont des types de filtres adaptatifs.

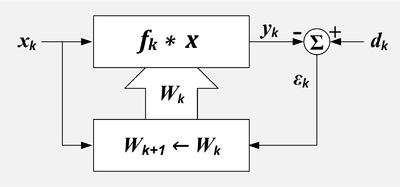
Il existe deux signaux d'entrée pour le filtre adaptatif : ${\displaystyle d_{k}}$ et ${\displaystyle x_{k}}$ qui sont parfois appelés respectivement entrée primaire et entrée de référence^[3]. L'algorithme d'adaptation tente de filtrer l'entrée de référence en une réplique de l'entrée désirée en minimisant le signal résiduel, ${\displaystyle \epsilon _{k}}$. Lorsque l'adaptation est réussie, la sortie du filtre ${\displaystyle y_{k}}$ est effectivement une estimation du signal souhaité.

${\displaystyle d_{k}}$ qui comprend le signal désiré plus les interférences non désirées et...

${\displaystyle x_{k}}$ qui comprend les signaux qui sont corrélés à certaines des interférences indésirables dans ${\displaystyle d_{k}}$.

k représente le nombre d'échantillons discrets.

Le filtre est contrôlé par un ensemble de L+1 coefficients ou poids.

${\displaystyle \mathbf {W} _{k}=\left[w_{0k},\,w_{1k},\,...,\,w_{Lk}\right]^{T}}$ représente l'ensemble ou le vecteur des poids, qui contrôlent le filtre au moment de l'échantillon k.

où ${\displaystyle w_{lk}}$ désigne le ${\displaystyle l}$'ième poids au k'ième temps.

${\displaystyle \mathbf {\Delta W} _{k}}$ représente le changement des poids qui se produit à la suite des ajustements calculés au temps d'échantillonnage k.

Ces changements seront appliqués après le temps d'échantillon k et avant d'être utilisés au temps d'échantillon k+1.

La sortie est généralement ${\displaystyle \epsilon _{k}}$ mais elle pourrait être ${\displaystyle y_{k}}$ ou même les coefficients du filtre^[4].

Les signaux d'entrée sont définis comme suit :

${\displaystyle d_{k}=g_{k}+u_{k}+v_{k}}$

${\displaystyle x_{k}=g_{k}^{'}+u_{k}^{'}+v_{k}^{'}}$

où :

g = le signal souhaité,

g' = un signal qui est corrélé avec le signal désiré g,

u = un signal non désiré qui est ajouté à g, mais qui n'est pas corrélé avec g ou g'

u' = un signal qui est corrélé avec le signal indésirable u, mais pas corrélé avec g ou g',

v = un signal indésirable (typiquement un bruit aléatoire) non corrélé avec g, g', u, u' ou v',

v' = un signal indésirable (typiquement un bruit aléatoire) non corrélé avec g, g', u, u' ou v.

Les signaux de sortie sont définis comme suit :

${\displaystyle y_{k}={\hat {g}}_{k}+{\hat {u}}_{k}+{\hat {v}}_{k}}$

${\displaystyle \epsilon _{k}=d_{k}-y_{k}}$.

où :

${\displaystyle {\hat {g}}}$ = la sortie du filtre si l'entrée était seulement g',

${\displaystyle {\hat {u}}}$ = la sortie du filtre si l'entrée était seulement u',

${\displaystyle {\hat {v}}}$ = la sortie du filtre si l'entrée était seulement v'.

Filtre FIR à ligne à retard à dérivation

Si le filtre variable a une structure de filtre à réponse impulsionnelle finie à ligne à retard à dérivation (en anglais : Tapped delay line FIR filter), alors la réponse impulsionnelle est égale aux coefficients du filtre. La sortie du filtre est donnée par

${\displaystyle y_{k}=\sum _{l=0}^{L}w_{lk}\ x_{(k-l)}={\hat {g}}_{k}+{\hat {u}}_{k}+{\hat {v}}_{k}}$

où ${\displaystyle w_{lk}}$ième désigne le lième poids au kième moment.

Cas idéal

Dans le cas idéal ${\displaystyle v\equiv 0,v'\equiv 0,g'\equiv 0}$. Tous les signaux non désirés dans ${\displaystyle d_{k}}$ sont représentés par ${\displaystyle u_{k}}$. ${\displaystyle \ x_{k}}$ consiste entièrement en un signal corrélé avec le signal indésirable dans ${\displaystyle u_{k}}$.

La sortie du filtre variable dans le cas idéal est la suivante :

${\displaystyle y_{k}={\hat {u}}_{k}}$ .

Le signal d'erreur ou fonction objectif est la différence entre ${\displaystyle d_{k}}$ et ${\displaystyle y_{k}}$

${\displaystyle \epsilon _{k}=d_{k}-y_{k}=g_{k}+u_{k}-{\hat {u}}_{k}}$. Le signal désiré g_k passe sans être modifié.

Le signal d'erreur ${\displaystyle \epsilon _{k}}$ est minimisé au sens du carré moyen lorsque ${\displaystyle [u_{k}-{\hat {u}}_{k}]}$ est minimisé. En d'autres termes, ${\displaystyle {\hat {u}}_{k}}$ est la meilleure estimation quadratique moyenne de ${\displaystyle u_{k}}$. Dans le cas idéal, ${\displaystyle u_{k}={\hat {u}}_{k}}$ et ${\displaystyle \epsilon _{k}=g_{k}}$, et tout ce qui reste après la soustraction est ${\displaystyle g}$ qui est le signal désiré inchangé avec tous les signaux non désirés éliminés.

Composantes du signal dans l'entrée de référence

Dans certaines situations, l'entrée de référence ${\displaystyle x_{k}}$ comprend des composantes du signal souhaité. Cela signifie que g' ≠ 0.

Une annulation parfaite du brouillage indésirable n'est pas possible dans ce cas, mais une amélioration du rapport signal/brouillage est possible. La sortie sera

${\displaystyle \epsilon _{k}=d_{k}-y_{k}=g_{k}-{\hat {g}}_{k}+u_{k}-{\hat {u}}_{k}}$. Le signal souhaité sera modifié (généralement diminué).

Le rapport signal de sortie/interférence a une formule simple appelée inversion de puissance.

${\displaystyle \rho _{\mathsf {out}}(z)={\frac {1}{\rho _{\mathsf {ref}}(z)}}}$.

où

${\displaystyle \rho _{\mathsf {out}}(z)\ }$ = rapport signal de sortie/interférence.

${\displaystyle \rho _{\mathsf {ref}}(z)\ }$ = rapport signal de référence/interférence.

${\displaystyle z\ }$ = fréquence dans le domaine z.

Cette formule signifie que le rapport signal de sortie sur interférence à une fréquence particulière est l'inverse du rapport signal de référence sur interférence^[5].

Exemple : Un restaurant de type fast-food dispose d'une fenêtre de type drive-up. Avant de se rendre à la fenêtre, les clients passent leur commande en parlant dans un microphone. Le microphone capte également le bruit du moteur et de l'environnement. Ce microphone fournit le signal primaire. La puissance du signal provenant de la voix du client et la puissance du bruit provenant du moteur sont égales. Il est difficile pour les employés du restaurant de comprendre le client. Pour réduire la quantité d'interférences dans le microphone primaire, un second microphone est placé à l'endroit prévu pour capter les sons du moteur. Il capte également la voix du client. Ce microphone est la source du signal de référence. Dans ce cas, le bruit du moteur est 50 fois plus puissant que la voix du client. Une fois que l'annuleur aura convergé, le rapport signal primaire/interférence sera amélioré de 1:1 à 50:1.

Combineur linéaire adaptatif

Le combineur linéaire adaptatif (ALC) ressemble au filtre FIR à ligne à retard adaptatif, sauf qu'il n'y a pas de relation présumée entre les valeurs X. Si les valeurs X provenaient des sorties, le filtre linéaire adaptatif (ALC) ne pourrait pas être utilisé. Si les valeurs X provenaient des sorties d'une ligne à retard à prises, alors la combinaison de la ligne à retard à prises et de l'ALC comprendrait un filtre adaptatif. Cependant, les valeurs X pourraient être les valeurs d'un réseau de pixels. Ou bien elles peuvent être les sorties de plusieurs lignes à retard. L'ALC trouve son utilité comme formateur de faisceau adaptatif pour des réseaux d'hydrophones ou d'antennes.

${\displaystyle y_{k}=\sum _{l=0}^{L}w_{lk}\_x_{lk}=\mathbf {W} _{k}^{T}\mathbf {x} _{k}}$

où ${\displaystyle w_{lk}}$ désigne le ${\displaystyle l}$'ième poids au k'ième temps.

L'algorithme LMS

Si le filtre variable a une structure FIR à ligne à retard taraudée, alors l'algorithme de mise à jour LMS est particulièrement simple. Typiquement, après chaque échantillon, les coefficients du filtre FIR sont ajustés comme suit^[6] :

pour ${\displaystyle l=0\dots L}$

${\displaystyle w_{l,k+1}=w_{lk}+2\mu \ \epsilon _{k}\ x_{k-l}}$

μ est appelé le facteur de convergence.

L'algorithme LMS n'exige pas que les valeurs X aient une relation particulière ; il peut donc être utilisé pour adapter un combineur linéaire ainsi qu'un filtre FIR. Dans ce cas, la formule de mise à jour s'écrit comme suit :

${\displaystyle w_{l,k+1}=w_{lk}+2\mu \ \epsilon _{k}\ x_{lk}}$

L'algorithme LMS a pour effet, à chaque instant, k, d'apporter un petit changement à chaque poids. La direction de la modification est telle qu'elle diminuerait l'erreur si elle avait été appliquée au moment k. L'ampleur de la modification de chaque poids dépend de μ, de la valeur X associée et de l'erreur au moment k. Les poids apportant la plus grande contribution à la sortie, ${\displaystyle y_{k}}$, sont modifiés le plus. Si l'erreur est nulle, alors il ne devrait pas y avoir de changement dans les poids. Si la valeur associée de X est nulle, alors la modification du poids ne fait aucune différence, il n'est donc pas modifié.

Convergence

μ contrôle la vitesse et la qualité de la convergence de l'algorithme vers les coefficients de filtre optimaux. Si μ est trop grand, l'algorithme ne convergera pas. Si μ est trop petit, l'algorithme converge lentement et peut ne pas être en mesure de suivre l'évolution des conditions. Si μ est grand mais pas trop pour empêcher la convergence, l'algorithme atteint rapidement l'état stable mais dépasse continuellement le vecteur de poids optimal. Parfois, μ est rendu grand au début pour une convergence rapide et ensuite diminué pour minimiser le dépassement.

Widrow et Stearns déclarent en 1985 qu'ils n'ont pas connaissance d'une preuve que l'algorithme LMS convergera dans tous les cas^[7].

Cependant, sous certaines hypothèses de stationnarité et d'indépendance, on peut montrer que l'algorithme convergera si

${\displaystyle 0<\mu <{\frac {1}{\sigma ^{2}}}}$

où

${\displaystyle \sigma ^{2}=\sum _{l=0}^{L}\sigma _{l}^{2}}$ = somme de toutes les puissances d'entrée.

${\displaystyle \sigma _{l}}$ est la valeur RMS de la ${\displaystyle l}$'ième entrée.

Dans le cas du filtre à ligne à retard taraudée, chaque entrée a la même valeur efficace car il s'agit simplement des mêmes valeurs retardées. Dans ce cas, la puissance totale est

${\displaystyle \sigma ^{2}=(L+1)\sigma _{0}^{2}}$

où

${\displaystyle \sigma _{0}}$ est la valeur efficace de ${\displaystyle x_{k}}$, le flux d'entrée^[7].

Cela conduit à un algorithme LMS normalisé :

${\displaystyle w_{l,k+1}=w_{lk}+\left({\frac {2\mu _{\sigma }}{\sigma ^{2}}}\right)\epsilon _{k}\ x_{k-l}}$ auquel cas le critère de convergence devient : ${\displaystyle 0<\mu _{\sigma }<1}$.

Filtres adaptatifs non linéaires

L'objectif des filtres non linéaires est de surmonter les limites des modèles linéaires. Il existe quelques approches couramment utilisées : Volterra LMS, Kernel adaptive filter (en), Spline Adaptive Filter ^[8] et le filtre adaptatif Urysohn^[9],[10]. De nombreux auteurs^[11] inclurent également les réseaux neuronaux dans cette liste. L'idée générale derrière le Volterra LMS et le Kernel LMS est de remplacer les échantillons de données par différentes expressions algébriques non linéaires. Pour le Volterra LMS, cette expression est la série de Volterra (en). Dans le filtre adaptatif Spline, le modèle est une cascade de bloc dynamique linéaire et de non-linéarité statique, qui est approximée par des splines. Dans le filtre adaptatif d'Urysohn, les termes linéaires dans un modèle

${\displaystyle y_{i}=\sum _{j=0}^{m}w_{j}\mathbb {N} -x_{ij}}$

sont remplacés par des fonctions linéaires par morceaux

${\displaystyle y_{i}=\sum _{j=0}^{m}f_{j}(x_{ij})}$

qui sont identifiées à partir d'échantillons de données.

Applications des filtres adaptatifs

• Annulation du bruit
• Prédiction du signal
• Annulation de la rétroaction adaptative
• Annulation d'écho

Implémentations de filtre

• en:Least mean squares filter
• Algorithme des moindres carrés récursifs
• en:Multidelay block frequency domain adaptive filter

Notes et références

Voir aussi

• en:2D adaptive filters
• Filtre
• Filtre de Kalman
• en:Kernel adaptive filter
• en:Linear prediction
• en:MMSE estimator
• Filtre de Wiener
• Méthode de Wiener-Hopf

Liens externes

• Notice dans un dictionnaire ou une encyclopédie généraliste :

  • Gran Enciclopèdia Catalana

• Portail de l’électricité et de l’électronique
• Portail des télécommunications
• Portail des mathématiques