Duplicació del cub
La duplicació del cub (també conegut com a problema delià) és un dels tres problemes irresolubles mitjançant una construcció amb regle i compàs de la geometria grega.
La duplicació del cub ha estat un dels problemes més importants i influents de la història de les matemàtiques, ja que molts dels intents per solucionar-lo han desembocat en l'aparició i desenvolupament de moltes eines i teories matemàtiques importants.
Juntament amb la quadratura del cercle i la trisecció de l'angle, formen els anomenats tres problemes especials de la matemàtica grega. Tot i que la quadratura del cercle es troba en altres cultures, probablement de forma independent, i ja havia estat tractat pels egipcis, la duplicació del cub i la trissecció de l'angle són d'origen purament hel·lènic.
Història
Segons la llegenda, els ciutadans d'Atenes van consultar a l'oracle d'Apol·lo de Delos el 430 aC. Volien saber com podien eliminar una plaga que estava arrasant les seves terres. L'oracle va respondre que per aturar la plaga havien de doblar la mida del seu altar. Els habitants d'Atenes van doblar la longitud de cada costat de l'altar i la plaga es va incrementar. La interpretació correcta era que havien de doblar el volum de l'altar i no simplement els seus costats. Aquest va ser realment un problema molt difícil de resoldre, però el 350 aC va ser resolt gràcies als esforços de Menaechmus. L'únic problema era que la plaga va acabar algunes dècades abans. Aquest problema s'anomena comunament "problema delià" degut a aquesta llegenda.[1]
Hipòcrates i la reducció al càlcul del mig proporcional
Hipòcrates de Quios (ca. 470 aC – ca. 410 aC) va ser un famós matemàtic, geòmetra i astrònom de l'antiguitat. Segons Aristòtil, encara que era un talentós geòmetra, era estult i presentava una manca de sentit comú en altres aspectes .
En l'àmbit de les matemàtiques, la seva major fita va ser que fou el primer matemàtic a escriure un llibre de geometria ordenat de manera sistemàtica, és a dir, demostrant els diferents teoremes a partir d'un conjunt reduït d'axiomes. Va ser anomenat Elements (precisament, és d'aquí d'on Euclides treu el nom del seu famós llibre), del qual només ha sobreviscut un petit fragment. D'altra banda, també se li atribueix ser el primer de fer servir el mètode de la reducció a l'absurd com a eina de demostració matemàtica.
En l'àmbit de la geometria en particular, a part d'estudiar el problema de la duplicació del cub, Hipòcrates també va estudiar altres problemes clàssics com el de la quadratura del cercle. Fins aleshores, mai s'havia aconseguit la quadratura d'una figura amb línies corbes i els matemàtics d'aquella època començaven a intuir que seria impossible. Hipòcrates, emperò, va aconseguir quadrar una figura amb línies corbes coneguda com a lluna d'Hipòcrates. En concret, va demostrar que l'àrea de la lluna de la figura és igual a l'àrea del triangle .
Quant a la duplicació del cub, Hipòcrates fou el responsable d'una reducció en el problema, de manera que l'enunciat fos aparentment més senzill. Tal reducció va fer pensar als diferents geòmetres que el problema podria ser resolt, però les seves suposicions eren infundades, ja que tal com es pot veure a la secció [sec:prova] és impossible aconseguir la duplicació del cub només amb regle (no marcat) i compàs.
Aquesta reducció consisteix a observar que el volum del cub augmenta seguint una progressió geomètrica cada cop que dupliquem la mida de l'aresta. Això implica que per trobar un volum igual al doble del volum inicial, la mida de l'aresta ha d'estar entre i , on és la mida inicial de l'aresta.
Com és una progressió geomètrica, cal utilitzar el mig proporcional (mitjana geomètrica) per tal de trobar aquest valor. I aquesta és la coneguda reducció d'Hipòcrates, la qual redueix el problema de la duplicació del cub al de trobar un mig proporcional.
Si denotem els dos mitjos proporcionals per i , aleshores, d'aquestes proporcions es té:
De manera que:
Per tant:
En conseqüència, es té que:
Així, és el valor de l'aresta d'un cub que té el volum doble d'un cub d'aresta . La construcció d'un segment d'aquesta longitud utilitzant regle (no marcat) i compàs és impossible, tal com es va poder demostrar utilitzant matemàtica més moderna.
El problema a l'antiga Grècia

Hi ha moltes maneres de construir en què s'utilitzen eines diferents al regle i al compàs. Realment, algunes d'aquestes eines poden ser construïdes amb regle i compàs però han de ser tallades del paper abans d'utilitzar-les. Per exemple, Sir Isaac Newton, va construir un regle amb una única unitat de distància marcada.
Arquirtes
Arquites de Tàrent (c. 428 aC - 350 aC) va ser un matemàtic grec, líder polític i filòsof que visqué durant la primera meitat del segle iv aC. Fou contemporani a Plató, amb qui mantingué certa relació. De fet, Plató assegura en la seva Carta Setena que Arquites mirà de salvar-lo de les urpes del tirà Dionís II de Siracusa enviant una nau a Sicília per rescatar-lo l'any 361 aC. Malgrat tot, la seva vinculació, personal i filosòfica, va ser complexa i hi ha mostres de desavinences entre ambdós.
Gran part de la seva obra està perduda, però se'n té constància per les referències que hi fan diversos autors. És considerat el primer a resoldre el problema. Existeixen indicis que va contribuir al desenvolupament de l'òptica i va establir les bases matemàtiques de la mecànica. Encara que tenim poca informació sobre la seva cosmologia, va desenvolupar l'argument més famós de la infinitud de l'univers en l'antiguitat. A més, és autor del que podria ser el primer text on s'identifica el grup de quatre ciències canòniques (aritmètica, geometria, astronomia i música), que més endavant, a l'Edat Mitjana, seria conegut amb el nom de quadrivium.
Resolució
La solució plantejada per Arquites té la particularitat que no està construïda sobre el pla, sinó a l'espai, i resulta de la intersecció de tres superfícies de revolució: un con recte, un cilindre i un tor.
Considerem dos segments , entre els quals haurem de trobar les mitjanes proporcionals. Prenent com a diàmetre, es traça una circumferència que tingui com a corda. Sobre aquesta circumferència s'aixeca un cilindre; en el cas d'Arquites, es tracta d'un semicilindre, perquè ho restringeix tot a un quadrant. En el pla perpendicular a la circumferència i que conté la recta , es dibuixa una semicircumferència sobre el diàmetre . Quan fem girar aquesta semicircumferència al voltant de la recta perpendicular al pla en el punt , obtenim un semitor de diàmetre interior nul que tallarà el cilindre en una determinada corba.
Per últim, considerem la recta tangent a en el pla de i anomenem el seu punt de tall amb la recta que conté el segment . Quan fem girar el triangle al voltant de l'eix , obtenim un con recte. La superfície del con es tallarà en un punt amb la corba que resultava de la intersecció del semitor i el semicilindre. Notem que el punt és part d'una semicircumferència ( la intersecció amb ) sobre la superfície d'aquest con perpendicular a i amb el diàmetre , on és l'altre punt comú amb la circumferència , també perpendicular a .
Recordem que per construir el semitor, hem fet girar una semicircumferència perpendicular a al voltant d'un eix perpendicular al pla per . Considerem en particular la semicircumferència que resulta d'aquesta rotació i que passa per ; anomenem el seu punt de tall amb el pla de . La semicircumferència en qüestió és, doncs, . Direm que el segment interseca amb la circumferència en el punt . Observem que és perpendicular al pla de , ja que és sobre el cilindre, que s'ha construït amb la circumferència com a base. Sigui el punt on es talla amb el diàmetre de la semicircumferència . Tracem els segments , , i .
Com que les semicircumferències i són perpendiculars al pla de , es compleix que és perpendicular al diàmetre . Per la proposició 35 del tercer llibre d'Euclides, es dona la igualtat
pel que és un angle recte, com també ho és (per estar inscrit en una semicircumferència). Això ens permet concloure que és paral·lel a. Per la semblança entre els triangles, es verifica:
és a dir,
de manera que , , i estan en proporció contínua. Així, i són les dues mitjanes proporcionals buscades. Veurem tot seguit que ens porten a la duplicació del cub en el cas particular que , però abans escriurem aquesta resolució en el llenguatge de la geometria analítica actual per comprovar que ens condueix al mateix resultat.
Si és l'eix , la recta perpendicular a que passa per en el pla és l'eix i la recta que passa per paral·lela a l'eix , llavors queda determinat per la intersecció de les superfícies
on i , que són respectivament el con recte, el cilindre i el tor.
De les dues primeres equacions, obtenim
i d'aquesta i la corresponent al tor,
o, cosa que és el mateix i com ja havíem indicat,
Tenim aleshores
En el cas particular que , obtenim , de forma que s'arriba a la duplicació del cub.
Èudox
Èudox de Cnidos (c. 408 aC - 355 aC) va ser un matemàtic, filòsof, astrònom i metge grec que va estudiar amb Arquites, de qui probablement adquirí l'interès per la duplicació del cub, així com per la teoria de nombres i la teoria de la música. Va fer importants contribucions a la teoria de la proporció, on va donar una definició que permetia longituds possiblement irracionals que s'havien de comparar de manera similar al mètode de multiplicació creuada utilitzat avui. La teoria desenvolupada per ell figura al cinquè volum dels Elements d'Euclides, on hi figura l'axioma d'Èudox en la definició 4. També hi va aparèixer la seva definició d'igualtat entre dues raons.
Una altra contribució notable d'Èudox a les matemàtiques fou un treball sobre la integració, utilitzant el mètode d'exhaustió i el seu propi treball sobre la teoria de la proporció. També va desenvolupar una teoria planetària que, influïda per la filosofia dels pitagòrics a través del seu mestre Arquites, descrivia un sistema basat en esferes giratòries, cadascuna al voltant d'un eix que passava pel centre de la Terra. Se'l considera, de fet, el pare de l'astronomia matemàtica.
Resolució
Sabem de la resolució d'Èudox per mitjà d'Eutoci, que en tenia una versió probablement errònia. En primer lloc, perquè Eratòstenes assegurava que el mètode d'Èudox usava línies corbes que a la solució no hi figuraven i, en segon lloc, perquè es tractava una proporció discreta com si fos contínua. Pel que fa a la primera observació d'Eutoci, podria explicar-se per la possibilitat que Èudox efectivament tractés amb corbes, però només hagués indicat un o dos punts d'aquesta suficients per al seu propòsit. Pel que fa a l'error, Èudox en sabia massa com per confondre una proporció contínua amb una discreta, i l'explicació més convicent seria que s'hagués transcrit malament la seva solució.
Molts anys després, Paul Tannery, al segle xix, va suggerir que la solució d'Èudox era en realitat una adaptació de la d'Arquites: una projecció de la construcció del seu mestre en el pla que conté la circumferència ABC. És a dir, una projecció de la intersecció entre el con i el tor al pla de ABC que, en intersecció amb la mateixa circumferència ABC, donava el punt M de la figura d'Arquites. És aquesta interpretació la que estudiem tot seguit.
La projecció en el pla de de la intersecció del con i el tor dona la igualtat
que, en coordenades polars amb l'origen i l'eix polar, equival a
Resulta senzill trobar qualsevol punt d'aquesta corba. Considerem la circumferència i siguin (el diàmetre) i (una corda) els dos segments dels que s'han de trobar dues mitjanes proporcionals. Tenim i . Si dibuixem on , perpendicular a , es dona

o bé
Sigui qualsevol punt de i unim . Si , aleshores
Ara tracem una circumferència de centre i radi que tallarà el diàmetre en un punt . Aixequem una perpendicular a aquest diàmetre que passi per i anomenem la intersecció amb la recta que conté el segment . Llavors
És a dir, si , tenim
i és un punt de la corba.
De forma equivalent podem representar qualsevol altre punt de la corba intersecció del con i el tor. Si la corba es troba amb la circumferència en , la longitud és la mateixa que la corresponent a la solució d'Arquites. Recordem que és una de les dues mitjanes proporcionals entre i . L'altra ( en la representació d'Arquites) s'obté ràpidament de la relació obtinguda a partir de la igualtat vista en la resolució d'Arquites. Obtingudes les dues mitjanes proporcionals entre i , el problema queda resolt.
Menecm
Menecm (c. 380-320 aC) fou deixeble d'Èudox de Cnidos i va donar-se a conèixer cap a la meitat del s.IV aC. Alguns autors consideren que va "fer la geometria més perfecte".
Menecm va trobar dues solucions al problema de la duplicació del cub. Les dues es basen a trobar un punt com a intersecció de dues còniques: una paràbola i una hipèrbola en el primer cas i dues paràboles en el segon. Aquestes solucions són mencionades a l'epigrama d'Eratòstenes: No talleu el con en les seccions de Menecm. De les solucions trobades juntament amb aquest fet, s'atribueix a Menecm el descobriment de les còniques, no conegudes amb els seus noms actuals atribuïts a Apol·loni, però sí com les corbes que complien les propietats necessàries per a resoldre el problema en qüestió.
Reduint-se a la idea d'Hipòcrates, les seves solucions busquen la proporció mitjana que ens dona el costat del cub duplicat. Si són dues mitjanes proporcionals entre dos segments , és a dir,
,
aleshores és clar que , i , on amb equacions cartesianes és fàcil reconèixer dues paràboles i una hipèrbola. Menecm no només va haver de veure això, sinó que també veure les propietats de les corbes trobades, com per exemple les assímptotes. A més, tot aquest formalisme que nosaltres utilitzem per a resoldre el problema no existia.
A part del descobriment de les còniques, no es coneix molta de la seva feina. és mencionat en altres obres com a col·laborador i s'extreu dels escrits de Procle que va escriure sobre el formalisme de les matemàtiques. Discutia les diferències entre principi i element, teorema i problema, i condicions suficients per als teoremes.
Com a curiositat, Menecm va ser tutor de geometria d'Alexandre el Gran. El rei li va demanar que li ensenyés una drecera per aprendre geometria. Menecm va contestar: Oh rei, per viatjar entre països hi ha camins reials i camins per ciutadans, però per arribar a la geometria hi ha només un camí per a tots. No se sap segur si això va ser així, ja que també hi ha la tendència a associar la frase a Euclides i el rei Ptolemeu, tot i que més coneguda la seva relació, seria posterior.
Resolució
A continuació explicarem les dues solucions de Menecm.
Primera solució

Suposem que i són dos segments tals que i els col·loquem formant un angle recte a . Suposem el problema solucionat, és a dir, tenim les dues mitjanes proporcionals
amb posat a continuació de i posat a continuació de . Ara completem el rectangle . Un cop fet això, tenim
és a dir, tenim que està sobre una paràbola amb vèrtex , eix i costat recte . Per altra banda, tenim
és a dir, tenim que està sobre una hipèrbola amb centre i assimptotes i . D'aquesta manera, per trobar el punt hem de construir una paràbola amb vèrtex , eix i costat recte i una hipèrbola amb assimptotes i tal que el rectangle construït pels segments i dibuixats sobre qualsevol punt de la corba paral·lels a una assimptota i tallant l'altra sigui semblant al rectangle format per i .
Així doncs, la intersecció de la paràbola i la hipèrbola ens donen el punt que soluciona
Segona solució

Com abans, suposem que el problema està resolt. Per tant, a partir de
tenim la relació
és a dir, tenim que està sobre una paràbola amb vèrtex , eix i costat recte , i també
és a dir, tenim que està sobre una paràbola amb vèrtex , eix i costat recte . Per trobar el punt doncs, hem de dibuixar les paràboles amb i per eixos i i per costats rectes respectivament.
La intersecció de les dues corbes ens dona el punt que ens resol la proporció mitjana buscada.
Plató
Plató (ca. 427 a.C. - ca. 347 a.C.) fou un filòsof grec, seguidor de Sòcrates i mestre d'Aristòtil. Va ser el fundador de l'Acadèmia on participaria activament en l'ensenyament. Durant els més de 900 anys de la seva duració, Aristòtil va acudir a l'Acadèmia des d'Estagira per estudiar filosofia al voltant del seu mestre.
Pel que fa al problema de la duplicació del cub, una de les grans qüestions és la solució coneguda com la màquina de Plató. Es tracta d'una solució mecànica i, per això, és difícil d'imaginar que Plató fos qui la donés. De fet, és lícit el dubte en tant que l'opinió que tenia Plató sobre aquest tipus de solucions era en detriment. Un exemple és aquest fragment escrit per Plutarc de Queronea (45 dC - 120 dC):
Plató va retreure als deixebles d'Èudox, Arquites i Menecm per recórrer a mitjans mecànics i instruments per resoldre el problema de duplicar el volum, ja que en el seu desig de trobar d'alguna manera dos mitjos proporcionals, van recórrer a un mètode que era irracional. En procedir d'aquesta manera, es perdia irremeiablement el millor de la geometria, per una regressió al nivell dels sentits, la qual cosa impedeix crear i fins i tot percebre les imatges eternes i incorpòries entre les que Déu és eternament Déu.
Hi ha dues teories referents a la utilització de la màquina de Plató per resoldre el problema de la duplicació del cub. Una és que Plató va inventar la solució mecànica per mostrar la facilitat del seu ús, però la teoria més acceptada és que la màquina de Plató fou inventada per un dels seus seguidors en l'Acadèmia.
En referència a la figura de la segona solució de Menecm, es veu que les línies rectes donades i els dos mitjos entre elles es mostren en ordre cíclic (a favor de les agulles del rellotge) com a línies rectes radials a i separades per angles rectes. Així és exactament la disposició de les línies en la solució atribuïda a Plató. Per tant, sembla probable que algú que tenia la segona solució de Menecm abans que ell estigués desitjant mostrar com la mateixa representació de les quatre línies rectes podria ser aconseguida amb una construcció mecànica com una alternativa a la utilització de les còniques.
Dibuixant les dues línies rectes abans esmentades, es defineixen en sentit dextrogir els segments , , i . De la mateixa manera que a la segona solució de Menecm, es té . Es pot observar que els angles i són rectes. El problema llavors és, donats i que formen un angle recte entre si, idear la resta de la figura per tal que els angles corresponents als vèrtexs i siguin rectes.
L'instrument utilitzat és un de semblant al que utilitzaria un sabater per a mesurar la longitud d'una sabata. L'angle és rígid, recte i està fet de fusta. és un puntal que, fixat a un pal i lliscant al llarg de , es pot moure mentre roman sempre paral·lel a o en angle recte amb .
A continuació, es col·loca el vèrtex rígid (que conté un angle recte) de manera que passi per , i es gira fins que el vèrtex es trobi en . Després, es fa lliscar el puntal mòbil , que roman sempre paral·lel a , fins que la seva vora (cap a ) passi per . Si ara el punt angular intern entre el puntal i la recta no es troba a la recta , s'ha de tornar a realitzar el procés de nou i el puntal s'ha de moure fins un punt de , com , tenint cura que durant tot el moviment les vores interiors de i passen per i respectivament i que el punt angular interior a es mou al llarg de la recta donada.
En la figura de Menecm es veu clarament que és possible que la muntura prengui la posició desitjada, on i són els mitjos entre i , i els angles , són angles rectes. Tot i això, no és fàcil d'aconseguir aquesta posició descrita.
L'assumpte pot ser considerat analíticament de la següent forma. Es pren qualsevulla altra posició de la construcció en la qual el puntal i passen per i respectivament, mentre es troba en la recta donada, però (punt angular entre el puntal i ) no està a la recta produïda . Es consideren i com els eixos i respectivament. Es dibuixa la recta , perpendicular a i es defineix com la intersecció de la recta produïda i .
Siguin , i tres segments de la construcció tractada. Aleshores o equivalentment; També, per semblança de triangles, , és a dir,
De l'equació s'obté , i multiplicant ambdues equacions es té by on, substituint el valor de , s'obté al lloc de una corba de tercer grau, . La intersecció, , d'aquesta corba amb l'eix dona .
El fet de ser una solució teòrica, l'atribuïda a Plató és més difícil que la de Menecm.
Erastòtenes
Eratòstenes (ca. 276 a.C. - ca. 194 a.C.) va ser un matemàtic, geògraf, poeta, astrònom i músic grec. És conegut per haver sigut la primera persona a calcular la circumferència de la Terra que, a més a més, va resultar ser bastant precisa. No només això, sinó que també va ser capaç de calcular l'obliqüitat de l'eclíptica, la distància de la Terra al Sol i també va inventar l'any de traspàs.
També feu una cronologia científica de tots els esdeveniments rellevants des de la Guerra de Troia.
Va ser una persona de gran influència en la seva època, qui rebutjà d'especialitzar-se en un únic camp. Això va fer que els seus crítics, com a mofa, l'anomenessin Beta (la segona lletra de l'alfabet grec), per tal de fer entendre que sempre era el segon en totes les seves investigacions .
En l'àmbit de les matemàtiques, se’l coneix per haver desenvolupat un algorisme que li permetia de trobar nombres primers. És conegut amb el nom de Sedàs d'Eratòstenes', certes modificacions del qual encara es fan servir avui en dia.
Respecte al problema de la duplicació del cub, Erastòtenes també va proposar una solució mecànica mitjançant tres figures planes que es poden moure en paral·lel una respecta l'altra i també respecte a la seva posició original entre dos regles en paral·lel. Pappus fa servir triangles, i Estoci paral·lelograms amb les diagonals dibuixades. En aquesta demostració, es faran servir triangles puix que és la solució més senzilla i elegant:
Suposi’s el marc delimitat per les rectes paral·leles i . La posició inicial dels triangles és la de la figura, on els triangles són , i .
A la figura, les línies paral·leles i són per les quals s'ha de trobar dos mitjos proporcionals i tots els triangles menys el triangle s'han mogut en paral·lel respecte a la seva posició original en direcció a , de manera que se superposen amb el triangle arribant a la posició en què passa per i el triangle a la posició , de manera que els punts i on i respectivament s'intersequen estan en una línia recta amb i .
Siguin , tals que es tallen en . Aleshores, i , mentre que . Per tant, es té que . De manera anàloga, es té que , de manera que , , i estiguin en proporció contínua i , són els dos mitjos proporcionals.
Nicomedes
Nicomedes (ca. 280 aC - ca. 210 aC) va ser un matemàtic grec de l'antiga Grècia. No es coneixen gaire detalls de la seva vida, només uns quants a partir de les referències en els seus treballs. Diversos estudis apunten que visqué aproximadament entre el 280 aC i el 210 aC, però només se sap amb certesa que va viure al mateix temps, o poc després, que Eratòstenes, ja que va fer una crítica del seu mètode per a la duplicació del cub. Eutoci va dir que Nicomedes:
...estava extraordinàriament orgullós del seu descobriment d'aquesta corba, contrastant-la amb el mètode d'Eratòstenes per trobar qualssevol nombre de mitjos proporcionals, del que objectava formalment que era impracticable i totalment contrari a l'esperit de la geometria.
Concoide de Nicomedes
Una concoide és una corba que deriva d'un punt fix (anomenat pol), una altra corba i una distància .
Per a cada recta que passa per i que interseca a la corba donada en , els dos punts d'aquesta recta de la qual estan a distància de formen part de la concoide. La concoide és, per tant, la cissoide de la corba donada i un cercle de radi i centre .
L'expressió més simple per a una concoide fa servir coordenades polars amb a l'origen: si és l'expressió de la corba donada, aleshores és l'expressió de la concoide. Si la corba és una recta, aleshores la concoide es coneix com a concoide de Nicomedes. En aquest cas, l'expressió de la concoide és o també en coordenades cartesianes: .
Solució proposada
Nicomedes va proposar una solució al problema de la duplicació del cub en el seu llibre Sobre les línies concoides de la qual estava especialment orgullós, ja que considerava que era molt millor que el mètode proposat per Eratòstenes.
Nicomedes va trobar una solució al problema per mitjà d'una concoide.
Siguin , dos segments que formen un angle recte:
- Completar el paral·lelogram .
- Bisecar els segments , en i respectivament.
- Ajuntar .
- Prolongar els segments i perquè es tallin en .
- Dibuixar formant un angle recte amb , de longitud tal que .
- Ajuntar i dibuixar paral·lel a ell.
- Des del punt , dibuixar , tallant en i prolongar fins a de manera que . Això es fa mitjançant una concoide en la qual és el pol, la corba inicial i la distància és .
- Ajuntar i prolongar i perquè es tallin en .
Aleshores, i son mitjanament proporcionals. En efecte, com que està bisecat en i perllongat a , es té que . Sumant a cada cantó, s'obté:
Per paral·lelisme, es té que . Però i , i per tant , cosa que implica que .
Però per construcció es té que i, per tant, i . Amb això i l'equació [eq:nicomedes], s'obté que i , el que vol dir que , mentre que al mateix temps es té que . Per tant, s'arriba al fet que o .
Apol·loni de Perge, Heró d'Alexandria i Filó de Bizanci
Aquests tres matemàtics grecs van donar essencialment la mateixa demostració, per això es presenten tots tres a la mateixa secció.
Apol·loni de Perge (ca. 262 aC - ca. 190 aC) va ser famós per la seva obra Sobre les seccions còniques, a més de ser qui va donar nom a l'el·lipse, la paràbola i la hipèrbola.
Sobre Heró d'Alexandria (ca. 10 dC - ca. 70 dC) se sap molt poca cosa. Només que es creu que va poder ser professor en el Museion d'Alexandria[2] ja que bona part dels seus escrits apareixen en forma d'apunts didàctics.
De Filó de Bizanci (ca. 280 aC - ca. 220 aC) se sap que va ser un escriptor grec els escrits del qual tractaren, entre altres coses, sobre mecànica. Investigacions recents apunten que va ser el primer en descriure un molí d'aigua de la història .
La demostració que van realitzar és la que es descriu a continuació:
Siguin , dos segments que formen un angle recte:
- Completar el rectangle i prendre el punt on les diagonals s'intersequen.
- Traçar un cercle amb centre i radi , de manera que el rectangle quedi circumscrit en ell.
- Traçar un cercle de centre , de tal manera que talli les prolongacions de i en i respectivament, de manera que , i estiguin alineats.
- Col·locar el regle de manera que passi per i rotar-lo respecte a fins que la vora intersequi les prolongacions de i en i respectivament, amb .
- Col·locar el regle de manera que passi per i rotar-lo respecte a fins que talli les prolongacions de i i el cercle per en punts , i de manera que i siguin iguals.
Clarament, totes tres construccions donen els mateixos punts i . En primer lloc, la prova que = és:
- Amb les construccions d'Apol·loni i Heró, es té que si és el punt mig de , aleshores . Sumant a ambdós membres, s'obté que . De manera similar, s'arriba al fet que , però com i , es té que .
- Amb la construcció de Filó, com que , es té que , però com el cercle passa per , aleshores i , i per tant .
A partir d'aquí i per simetria de triangles, es té que , cosa que implica que i, per tant, es conclou que .
Diocles i la Cissoide
Diocles (ca. 240 aC - ca. 180 aC) va ser un destacat geòmetra contemporani a Apol·loni de Perge. A Diocles se li atribueix la comprovació de la propietat de la paràbola (un mirall parabòlic reflexa de forma paral·lela els raigs emesos des del seu focus, cosa molt important en les antenes de satèl·lits). Una de les seves obres més destacades és Sobre els miralls ustoris que ha tingut una gran influència en els matemàtics àrabs posteriors. Al llibre, destaca l'habilitat de Diocles en l'ús de les seccions còniques.
La cissoide
La Cissoide de Diocles és una corba generada per la resta del vector posició d'una recta paral·lela a l'eix , que passa pel punt , i el radi vector d'una circumferència de radi i centre en .
En coordenades cartesianes, la cissoide té la següent expressió: I en coordenades polars:
Diocles va introduir aquesta corba per a resoldre el problema de la duplicació del cub.
Mètodes més enllà de l'antiga Grècia
Diferents autors moderns van suggerir mètodes de la duplicació del cub. Entre aquests, destaquen els noms de Viète, Descartes, Fermat, Huygens i Newton.
De fet, Descartes va demostrar que qualsevol problema geomètric que dona una equació cúbica es pot reduir a la duplicació del cub o a la trisecció de l'angle, com ja havia anunciat prèviament Viète.
Per la seva banda, Fermat que, tot i escriure la seva solució abans que Descartes, aquesta no va ser coneguda fins després de la seva mort, va anar més lluny considerant el cas de n mitjanes proporcionals.
Com veurem més endavant, en el segle xix es va demostrar la impossibilitat de resoldre el problema amb regle i compàs; tot i així, podem encara trobar aproximacions prou bones de l'arrel cúbica en ple segle XX com és el cas de la proposada per Finsler (1937/38).
François Viète
François Viète va néixer l'any 1540 a Fontenay-le-Comte (es desconeix la data exacta) i va morir a París el 13 de desembre de 1603. Tot i que Viète mai va ser matemàtic professional va realitzar diverses publicacions, entre les quals destaquem Supplementum geometricae (1593), on va presentar solucions geomètriques per a la duplicació del cub i la trisecció de l'angle. En particular, demostrarem la Proposició V, on estudia la duplicació del cub.
Proposició V: donades dues línies rctes, trobar les dues mitjanes proporcionals entre elles.
Siguin i els dos segments donats ( major que ), hem de trobar les dues mitjanes proporcionals entre i . Tracem d'entrada una circumferència amb centre i radi igual a la meitat de la longitud de . Situem dos punts sobre la circumferència, i , de manera que el segment sigui igual a la longitud de i extenem fins a fent que sigui el doble de .

A continuació unim i i tracem un segment paral·lel a DA, BE, de longitud indefinida. Extenem DB també indefinidament fins al punt F i tracem una línia recta KAIGH que talli la circumferència en els punts I i K i els segments BE i BF en els punts G i H de manera que AB=GH. Com que DA i BG són paral·lels, els triangles HGB i HAD són semblants i per tant:
,
a més, com que IK=2AB=2HG i BD=2BC se satisfà:
A partir d'aquestes expressions obtenim:
d'on
Com que GH=AI, aleshores HI=GA i per tant:
Així doncs, des del punt H, exterior a la circumferència, s'han construït dos segments que la tallen (HK i HC), de manera que el producte de les seves parts exteriors (HI i HB) és igual al producte de les seves parts interiors (IK i BC). És per això que IK, HB, HI i BC estan en proporció contínua. En tant que IK i BC tenen la mateixa longitud que els segments Z i X respectivament, hem trobat les dues mitjanes proporcionals entre Z i X, HB i HI.
René Descartes
René Descartes (1596-1650) fou un filòsof, matemàtic i físic francès considerat el pare de la geometria analítica i de la filosofia moderna. Aquesta soluci\'o per al problema de trobar dues mitjanes proporcionals apareix en el llibre tercer de la seva obra La Geometria. La demostració que mostrarem, però, serà la que ofereix Claude Rabuel en el seu llibre Comentaris sobre La Geometria de M.Descartes ja que Descartes utilitza resultats previs que caldria analitzar amb detall.
Partint de dos segments donats a,q volem trobar dues mitjanes proporcionals. Hem de dibuixar una paràbola amb un vèrtex A i un punt C sobre l'eix de simetria d'aquesta tal que AC=a/2 i amb una distància focal igual a a/4. Ara fem la perpendicular a AC que passi per C i trobem un punt E tal que CE=q/2. Tracem la circumferència de centre E i que passa per A i anomenem F el punt de tall de la paràbola amb la circumferència. Tracem la perpendicular a AC que passi per F i talli l'eix de simetria de la paràbola a L i obtindrem que FL i LA són les dues mitjanes proporcionals buscades.

Per a la demostració considerarem una recta perpendicular a EC i que passi per E, direm que M és el punt de tall amb la recta que conté FL. Anomenem FL=z i observem els següents resultats
La primera propietat és conseqüència directa de les propietats de la paràbola i la resta són pel teorema de Pitàgores. Escrivim les igualtats anteriors en termes de a,q i z=FL.
Com que EF=EA per ser radis de la circumferència, obtenim
i com que obtenim la igualtat com a solució per a la duplicació del cub. En la figura hem pres a=1 i q=2 de manera que el segment .
Chritiaan Huygens
Christiaan Huygens (1629 - 1695) va ser un astrònom, físic i matemàtic holandès. El metode exacte per construir el cub de volum el doble que un de costat OA=a consisteix en dibuixar el mig cercle de radi OA i considerar la corda DA=OA. Tracem CD, on C és el diàmetre oposat a A. Aleshores, tracem una corda AE tal que interseca el segment CD en el punt F de tal manera que DF=CE. Així doncs, trobem que .

Suposem que tenim OA=1 i busquem x=AF. Pel teorema de Pitàgores, tenim la relació
Com que els triangles ADF i CEF tenen els mateixos angles, podem escriure tots els costats en funció de x i trobar relacions entre els costats. En particular, ens interessen aquestes dues
ja que aleshores aconseguim
i l'única solució possible per a la longitud d'un costat és .
Huygens va proposar un mètode basat en aquest realitzable amb regle i compàs per a trobar una bona aproximació de . Si construim de manera equivalent els punts O, A, C i D, trobem el punt E' fent que l'angle COE' sigui 45° i el punt F' com la intersecció de CD i AE'. La nostra aproximació serà el segment AF'.
Com que
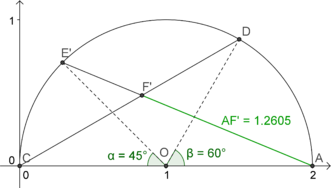
tenim
Aleshores,
Veiem que l'error és .
Isaac Newton
Isaac Newton (1642-1727) va ser un físic, filòsof i matemàtic anglès que va fer grans aportacions a la física establint les bases mecànica clàssica i a les matemàtiques desenvolupant el càlcul integral i diferencial. La seva obra més coneguda són els Principia, on descriu la llei de la gravitació universal i enuncia les tres lleis de la física que porten el seu nom. Aquesta solució per a la duplicació del cub la podem trobar a Aritmetica Universalis (1707).

Partint del segment AB=a donat, es traça la perpendicular BR i es construeix el segment BT de manera que ABT formin un angle de 120 graus. Seguidament, prenem el punt D del segment BT de manera que si C és la intersecció de AD amb BR es tingui que CD=AB. Tracem la perpendicular a BR que passi per D i talli BR en el punt E. Sota aquestes condicions i prenent BC=b, CE=y, DE=x i AC=c tenim les igualtats següents:
La primera propietat és degut al fet que ABC i DEC són triangles semblants, la segona és per la definició de la tangent i la tercera ve donada pel teorema de Pitàgores. Si elevem al quadrat la segona equació i utilitzem la tercera, obtenim
Així doncs, el cub de costat c tindria el doble de volum que el de costat a.
Paul Finsler
Paul Finsler (1894-1970) va ser un matemàtic Alemany, professor a la Universitat de Zúric, que va treballar en diversos aspectes de la geometria diferencial. Va donar un mètode aproximat per trobar el valor de .

Sigui A,B,C,D una cara d'un quadrat de costat unitat. Tracem els punts M i N a distàncies 4 i 8 respectivament respecte a A. Construim un cercle de radi AC centrat en A i un altre centrat en M de radi AM. Anomenem E a un punt de la intersecció d'aquests dos cercles i en tracem un tercer centrat a N de radi NE. Anomenem F la intersecció del cercle amb el segment AB i obtenim que 10·AF és una aproximació de .
Per a la demostració prendrem l'eix x en AB i l'eix y en AD de manera que les equacions dels dos primers cercles són i . El punt E que resulta com a intersecció d'aquests dos cercles tindrà per coordenades . El cercle centrat a N amb radi NE tindrà per equació i F serà la solució de l'equació quan imposem que y=0. Les solucions de són i la que es troba dins el segment AB correspon a . Aleshores, és una bona aproximació de l'arrel cúbica de 2.
De manera que l'error absolut és de l'ordre de .
La irresolubilitat en regle i compàs
Per comprendre aquest bloc és recomanable conèixer resultats bàsics d'extensions de cossos.
Construccions amb regle i compàs
Considerem un conjunt de punts en el pla euclidià , a partir del qual construirem d'altres punts emprant dues operacions que definim tot seguit. Donat el conjunt , les operacions possibles amb regle i compàs són les següents:
- Traçar una recta que passi per dos punts de .
- Traçar una circumferència, el centre de la qual sigui un punt de , de radi igual a la distància entre dos punts de .
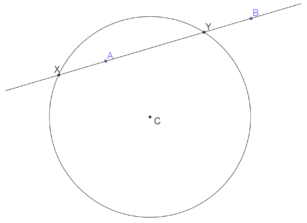
Els punts que resulten de la intersecció de dues rectes o circumferències, traçades amb les operacions 1 o 2, s'anomenen construïbles en un pas a partir de .
Un punt s'anomena construïble a partir de si existeix una seqüència finita de punts de de forma que per a tot , el punt és construïble en un pas a partir del conjunt
La translació a la teoria de cossos és d'allò més natural: a cada pas de la construcció d'un punt li associem el subcòs de generat per les coordenades del punt construït. Definim com el subcòs de generat per les coordenades x i y dels punts de . Si té coordenades , inductivament definim com el cos resultant d'adjuntar i en , és a dir,
i, per construcció, és evident que
Un lema que no demostrarem, ens diu que, mantenint la notació anterior, i són zeros en de polinomis quadràtics en .
Teorema: Sigui el subcòs generat per les coordenades dels punts del conjunt de . Si és un punt construïble a partir del conjunt , els graus i són potències de 2.
Demostració: Pel lema anterior, tenim
segons si el polinomi quadràtic del qual és arrel és irreductible o no. Igualment,
de manera que, per la fórmula dels graus,
i de fet es pot demostrar que el valor 4 no s'assoleix mai, però això no ens cal.
Per tant, recordant que , tenim que és una potència de 2. Per inducció, es veu fàcilment que és potència de 2. Per la fórmula dels graus,
d'on se segueix que ha de ser una potència 2. Anàlogament, també ha de ser una potència de 2.
Wantzel i la irresolubilitat del problema
Cal tenir en compte que Johann Carl Friedrich Gauss (1777 - 1855) en les Disquisitiones Arithmeticæ va aplicar la teoria dels polinomis ciclotòmics a la constructibilitat dels polígons regulars amb regle i compàs, i també es creu que va afirmar que els problemes de la duplicació del cub i la trisecció de l'angle no es podien resoldre amb regle i compàs, però no ho va demostrar. Wantzel va ser el primer en demostrar-ho, en aquest article, i tot i que Charles Sturm (1803 - 1855) posteriorment va donar proves millors, no les va publicar.
Pierre-Laurent Wantzel va néixer el 5 de juny del 1814 a París i va morir el 21 maig del 1848, també a París. El seu pare fou professor de matemàtiques aplicades a l'École speciale du Commerce.
Wantzel és famós pels seus estudis en la resolució d'equacions per radicals. El 1837 Wantzel va descriure la manera de determinar si un problema geomètric es pot resoldre amb regle i compàs en un article en el Journal de Mathématiques Pures et Appliquées, fundat per Joseph Liouville (1809 - 1882), basant-se en altres autors, com Évariste Galois.
L'any 1845 Wantzel, continuant amb els seus estudis sobre les equacions, va donar una nova prova de la impossibilitat de resoldre totes les equacions algebraiques per radicals.
Resolució
Teorema: El cub no pot ser duplicat mitjançant construccions amb regle i compàs. (Wantzel, 1837)
Demostració: Donat un cub qualsevol, establim el seu costat com a unitat de l'eix x. Aleshores el volum és de (unitats), i el nostre objectiu és duplicar-lo a . Podem assumir que tenim i, com que amb els punts i es pot construir qualsevol nombre racional,[3] . Suposem que el punt , amb , fos construïble. Pel teorema anterior, seria una potència de 2. Però és arrel del polinomi , que és irreductible sobre per ser un polinomi de grau amb cap arrel en . Així doncs, com que aquest polinomi és irreductible i s'anul·la en , és el polinomi mínim de sobre i, per la igualtat entre el grau d'aquest i el grau de l'extensió, , que no és potència de 2. Per tant, el punt no és construïble i no és possible duplicar el volum del cub amb regle i compàs.
Referències
Enllaços externs
- Doubling the cube. J. J. O'Connor and E. F. Robertson in the MacTutor History of Mathematics archive.
- To Double a Cube -- The Solution of Archytas. Excerpted with permission from A History of Greek Mathematics by Sir Thomas Heath.
- Delian Problem Solved. Or Is It? a cut-the-knot (anglès)








![{\displaystyle a^{3}=2s^{3}\Rightarrow a={\sqrt[{3}]{2}}s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4e33e6d39b2b9d66e06adcfa6223399907fe605)
![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)

















































































































































































































![{\displaystyle FL={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc14fb319989f726e1fd155bcd26d7b75177f53)
![{\displaystyle AF={\sqrt[{3}]{2}}a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ea986a762337d84295e42a7cb1d48b7891453c4)




![{\displaystyle x=AF={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e186731c36e4dfea8daa15ef5795ddfe12f789d)




![{\displaystyle |{\sqrt[{3}]{2}}-AF'|=0,00055}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6f5b90a8a0fc0e9cead375a11332d5e98b3ede5)












![{\displaystyle {\sqrt[{3}]{2}}=1.259921049\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec82b4346e77a50f4094c6d10a04fd0fb432bcc)

![{\textstyle \Delta =|{\sqrt[{3}]{2}}-(10\cdot (8-{\sqrt {62}})|=2\cdot 10^{-7}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2be252aeac771b9c0932f9b0aef113b36a2b8a9a)

















![{\textstyle [K_{0}(x):K_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10d4eaee6d74b39392447f52c3fe6571037d291d)
![{\textstyle [K_{0}(y):K_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0e90239e299540d36a4479f9cefb32aa34ccb0)
![{\displaystyle [K_{i-1}(x_{i}):K_{i-1}]=1{\text{ o }}2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4afb78ac7c10a1650c7313d7ae58fe8efd781701)
![{\displaystyle [K_{i-1}(y_{i}):K_{i-1}]=1{\text{ o }}2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fba4b0ef231704b398b324175e6b8eb3190ca83)
![{\displaystyle [K_{i-1}(x_{i},y_{i}):K_{i-1}]=[K_{i-1}(x_{i},y_{i}):K_{i-1}(x_{i})][K_{i-1}(x_{i}):K_{i-1}]=1,2{\text{ o }}4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61f060fe51848224b15e14a102ab43ab2459d33d)
![{\textstyle [K_{i}:K_{i-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa2696f9b4cd4e37093599af99b365d5d195749e)
![{\textstyle [K_{n}:K_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef023f90f11d0ef8c3556fbc1db01ab51767e79a)
![{\displaystyle [K_{n}:K_{0}]=[K_{n}:K_{0}(x)][K_{0}(x):K_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e8ff9c2bc77b3a134b68fc3f8b9ba79c5b9e5e3)








![{\textstyle [\mathbb {Q} (\alpha ):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af99954ef2fd48aa6ef7a4cdd6e46567492b08c8)

![{\textstyle X^{3}-2\in \mathbb {Q} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/576f40810192ed9f4953c7e9c8310f0b79288432)


![{\textstyle [\mathbb {Q} (\alpha ):\mathbb {Q} ]=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c2e0e432b79e69e1356b3f8dc8d454136e64616)
